数值分析——误差的来源与分类、误差的基本概念(绝对误差、相对误差、有效数字)
误差
误差分析实际上是让数据更加可靠,更加有效,从理论分析上就是考虑误差的收敛性,稳定性。
误差的来源与分类
模型误差
数学模型与实际问题之间存在的误差称为模型误差
观测误差
一些由观测得到的物理量,比如温度、长度等,这些观测值也存在误差,这种误差称为观测误差.
模型误差与观测误差不能改变
截断误差
在计算中,通过有限过程的计算结果代替无限过程的结果而造成的误差,称为截断误差. 这是计算方法本身存在的误差,所以也称为方法误差.
eg:
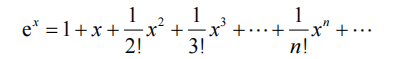
当用计算机求时,只能选有限个项作为ex的近似值,也就是:
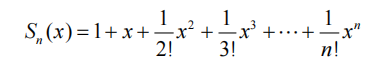
由泰勒定理,部分和Sn(x)作为ex的近似值的余项是:
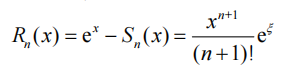
其中,
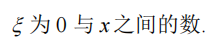
Rn(x)就是把前n项和Sn(x)作为ex的近似值产生的截断误差。
舍入误差
计算过程中取有限位数字进行运算而引起的误差称为舍入误差.。
eg:
用 3.14159265358 近似代替 π,产生的误差
R=π-3.14159265358=0.000000000009793····
就是舍入误差
误差的基本概念
绝对误差
假设x*为准确值,x是 x*的一个近似值,那么近似值x的绝对误差e(x)就是:
e(x)=x*-x
绝对误差=准确值-近似值
错误的英语是error,所以用首字母e表示误差
绝对误差限
精确值x*是未知的,只知道范围即可,也就是:
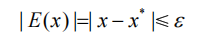
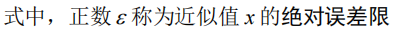
有时候也可以表示为:
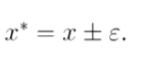
相对误差
假设x*是准确值,x是x*的一个近似值,那么er(x)相对误差就是:
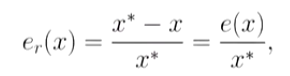
er(x)=e(x) / x*
相对误差=绝对误差 / 精确值
通常,x的相对误差的计算为:
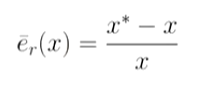
也就是原来相对误差计算式子中的分母x* 。因为难以知晓,所以用一个近似值x来代替精确值x*。两者之间将等式做差可以知道它们相差的是一个高阶无穷小量,所以可以近似的看为是相等的关系
相对误差限

有效数
近似值x的绝对误差限是其某一位的半个单位,且高位直到x的第一位非零数字之间共有n维,那么就称这个x有n位有效数字,这n位有效数字来表示的近似值就是有效数。
概念有点难以理解,那么就举个🌰
假设一个近似值x为:
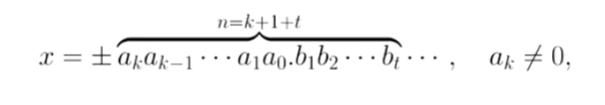
如果有
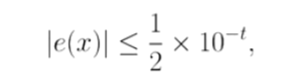
那么x就有n个有效数字。
也就是说要从左边第一个不是 0 的数字往右边一直数到第 t 位,中间有多少位那么就是有多少个有效数字,此时就可以用这些有效数字表示近似值x了
eg:
π = 3.1415926····
假如,令 x1 = 3.14作为 π 的一个近似值,则
| π - x1 |=3.14159··· - 3.14 = 0.00159···≤½ *10-2
此时,10的次方是 - 2 次,就代表是X1小数点后的第二位,也就是 4 的位,3.14 从左边第一个不为 0 的数字开始数,就是 3,1,4。数到 4 时一共数了三次,就说明有三个有效数字,那么就代表x1有 3 个有效数字,因此x1 = 3.14是有效数。
x1是有效数,有三个有效数字,3,1,4
假如令 x2 = 3.1415,那么
| π - x2| = 3.14159···-3.1415 = 0.00009···
又因为
0.00009 < 0.0005 ≤ ½ * 10-3
此时,10 的次方是 - 3 次,就表示从左边开始第一个不为 0 的地方开始数,也就是从3开始数,一直数到小数点后的第三位,也就是从左往右数的第二个 1 的位置结束,一共数了四次,有3,1,4,1,因此,表示x2只有四个有效数字,分别是3,1,4,1,因为x2多了一位无效数字5,所以x2不是有效数。
x2不是有效数,只有四个有效数字,因为多了一个无效数字5
结论:
1,如果 x 有 n 位有效数字,那么它的相对误差满足:
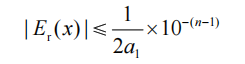
2,如果 x 的相对误差满足:
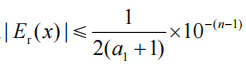
那么 x 至少有 n 位有效数字
a1 是第一个不为 0 的数
有效数字的位数越多,相对误差就越小
根据以上两个式子可以由 n 退出 a1 ,或者 a1 推出 n 。
数值计算设计法则
1,简化计算步骤,减少运算的次数
2,避免两个相近的数相减
3,防止大数“吃掉”小数
4,避免用绝对值很小的数作为除数
5,用数值稳定性好的算法
*未完待更,正在努力更新中ing····· *
:)
