《潮汐调和分析原理和应用》之四S_Tide使用2

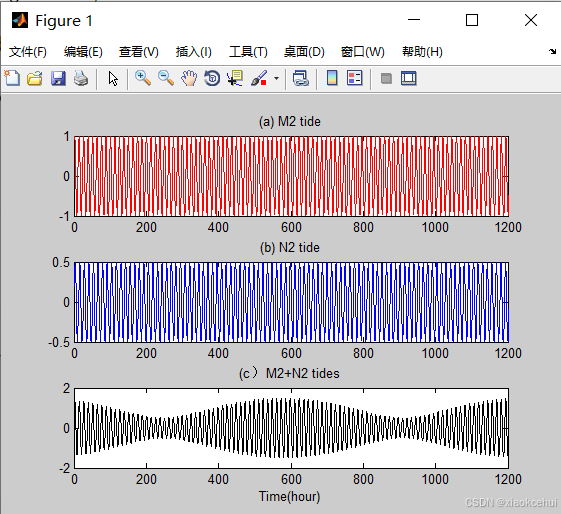
1、M2和N2分潮叠加

基于S_TIDE的s_construct函数构造的M2和N2分潮，可以把M2和N2分潮叠加后的结果理解为M2振幅的27.55天（661.2小时）的调制，即如果不在调和分析模型里分辨N2分潮，M2振幅的时间变化会存在27.55天周期。

function [sumconsti,consti]=s_construct(tides,amp,pha,dt,length);
%Haidong Pan(Ocean University of China) 2020/12/24   
%email:1027128116@qq.com      panhaidong_phd@qq.com     
% S_TIDE users QQ group number 485997351
%the input:
%     tides:the names of input tidal constituents
%     amp: the amplitudes of input tidal constituents
%     pha: the phases of input tidal constituents
%     dt: the interval of constructed time series (unit:hour)
%     length: the total length of constructed tiem series
%
% the output:
%    consti: the water levels induced by individual tidal constituent
%    sumconsti: the sum of tidal water levels（分潮是为
%
%see s_demo.m for examples
nobsu=length-rem(length-1,2);% makes series odd to give a center point
t=dt*([1:length]')-ceil(nobsu/2);  % Time vector for entire time series,

load t_constituents
J=size(amp);JJ=J(find(J>1));
if isempty(JJ)==1
JJ=1;
end
if iscell(tides)==1
for i=1:JJ
ju(i)=strmatch(upper(tides(i)),const.name);
fu(i)=const.freq(ju(i));
end
end
consti=zeros(JJ,length,'double');
t=t';
for j=1:JJ
aa=amp(j)*cosd(pha(j));bb=amp(j)*sind(pha(j));
consti(j,:)=aa*cos((2*pi)*t*fu(j))+bb*sin((2*pi)*t*fu(j));
end
sumconsti=sum(consti);
if JJ==1
sumconsti=consti; 
end

%M2和N2分潮叠加

tides={'M2';'N2'};

amp=[1,0.5];pha=[180,90];dt=1;length=8760;

[sumconsti,consti]=s_construct(tides,amp,pha,dt,length);

subplot(3,1,1);plot(consti(1,:),'r-');xlim([0 1200])

title('(a) M2 tide');

subplot(3,1,2);plot(consti(2,:),'b-');xlim([0 1200])

title('(b) N2 tide');

subplot(3,1,3);plot(sumconsti,'k-');xlim([0 1200])

title('(c）M2+N2 tides');xlabel('Time(hour)')

2、交点因子和交点订正角

月球升交点的黄经N存在的18.61年循环会调制太阴分潮的振幅和迟角，通过积化和差产生一些小分潮，而将主要分潮和这些小分潮分开需要最少18.61年的数据，显然，很多验潮站的水位观测无法满足这个条件，故引入交点因子f和交点订正角u来消除18.61年的影响。

%交点因子和交点订正角的计算

function [ff,uu,vv,N,s,h,p,pp]=s_nodal_cal(tides,stime,etime,dt,latitude)
% written by Haidong Pan, 2021/03/16
% calculate the nodal factor and angle for input constituents
%-----input-----
% tides    the name of input tidal constituents (in the form of cell)
% stime    start time
% etime    end   time
% dt       sampling interval (day)
% latitude latitude should not be zero)
%----output-----
% ff    nodal factor
% uu    nodal angle                         
% vv    astronomical phase
% N     mean longitude of the ascending node
% s     mean longitude of the moon
% h     mean longitude of the sun
% p     mean longitude of the lunar perigee 
% pp    mean longitude of the perihelion (solar perigee)   
% see s_demo.m for example or see the example below
%
%[ff,uu]=s_nodal_cal({'K1';'O1';'M2'},[1920,01,01],[2020,01,01],365,10);
% subplot(2,1,1);
% plot(ff(1,:),'k');hold on;plot(ff(2,:),'r');plot(ff(3,:),'b')
% legend('K1','O1','M2');
% set(gca,'XTick',0:25:2020)
% set(gca,'XTickLabel',{'1920','1945','1970','1995','2020'})
% title('(a) nodal factor')  
% subplot(2,1,2);
% plot(uu(1,:),'k');hold on;plot(uu(2,:),'r');plot(uu(3,:),'b')
% set(gca,'XTick',0:25:2020)
% set(gca,'XTickLabel',{'1920','1945','1970','1995','2020'})
% title('(b) nodal angle')
%
disp(['******calculating astronomical phase V, the nodal phase modulation U, and the nodal amplitude correction F*********'])
disp(['***********************accurate nodal/satellite corrections need lots of time!*************************************'])
disp(['***********written by Haidong Pan***********'])
load t_constituents
if iscell(tides)==1          
for i=1:length(tides)
ju(i)=strmatch(upper(tides(i)),const.name);
end
end
Lor=datenum(etime)-datenum(stime);
num=floor(Lor/dt);
%ff=zeros(length(ju),num,'double');uu=ff;vv=ff;N=ff;s=ff;h=ff;p=ff;pp=ff;
for i=1:num
days=datenum(stime)+(i-1)*dt;
[v,u,f,astro]=t_vuf('nodal',days,ju,latitude);
ff(:,i)=f(:);
uu(:,i)=360*u;
vv(:,i)=360*v;
N(i)=astro(5)*-360; 
s(i)=astro(2)*360;
h(i)=astro(3)*360;
p(i)=astro(4)*360;
pp(i)=astro(6)*360;
end
N(N<0)=N(N<0)+360;

%iscell的解释

m=5 %m为1×1的数值
m='5' %m为1×1的字符
m='h' %m为1×1的字符
m="h" %m为1×1字符串
m="hello" %m为1×1的字符串
m="hello world" %m为1×1的字符串
m='hello' %m为1×5的字符数组
m='hello world' %m为1×11的字符数组
m={'hello'} %m为1×1的元胞数组
m={'hello','world'} %m为1×2的元胞数组

%t_vuf函数

function [v,u,f,astro]=t_vuf(ltype,ctime,ju,lat);
% T_VUF Computes nodal modulation corrections.
% [V,U,F]=T_VUF(TYPE,DATE,JU,LAT) returns the astronomical phase V, the 
% nodal phase modulation U, and the nodal amplitude correction F at
% a decimal date DATE for the components specified by index JU 
% at a latitude LAT.
%
% TYPE is either 'full' for the 18.6 year set of constitunets, or 'nodal'
% for the 1-year set with satellite modulations.
%
% If LAT is not specified, then the Greenwich phase V is computed with
% U=0 and F=1. 
%
% Note that V and U are in 'cycles', not degrees or radians (i.e.,
% multiply by 360 to get degrees).
%
% If LAT is set to NaN, then the nodal corrections are computed for all
% satellites that do *not* have a "latitude-dependent" correction 
% factor. This is for compatibility with the ways things are done in
% the xtide package. (The latitude-dependent corrections were zeroed
% out there partly because it was convenient, but this was rationalized
% by saying that since the forcing of tides can occur at latitudes
% other than where they are observed, the idea that observations have 
% the equilibrium latitude-dependence is possibly bogus anyway).
% T_VUF 计算交点调制校正量
% [V,U,F] = T_VUF(类型,日期,JU,纬度) 返回在十进制日期DATE下，
% 针对JU索引指定分量在纬度LAT处的天文相位角V、交点相位调制U
% 及交点振幅校正因子F
%
% 类型参数可选：
% 'full' 采用18.6年周期分潮组
% 'nodal' 采用包含卫星调制的1年周期分潮组
%
% 若未指定LAT参数，则计算格林尼治相位V（此时U=0且F=1）
%
% 注意：V和U的单位为"周角"（非度或弧度，需乘以360转换为度）
%
% 若将LAT设为NaN，则仅计算不依赖纬度校正因子的卫星分量校正值。
% 此特性用于保持与xtide软件包的兼容性（该包中出于便利性考虑，
% 直接忽略了纬度依赖性校正；其理论依据是：由于潮汐驱动力可能源自
% 观测点以外的纬度区域，认为观测结果应遵循平衡潮纬度依赖性的
% 理论假设本身可能存在谬误）
% R. Pawlowicz 11/8/99
%               1/5/00 - Changed to allow for no LAT setting.
%              11/8/00 - Added the LAT=NaN option.
%              10/02/03 - Suuport for 18-year (full) constituent set.
% Version 1.2

% Get all the info about constituents.

% Calculate astronomical arguments at mid-point of data time series.
[astro,ader]=t_astron(ctime);

if strcmp(ltype,'full'),

  [const]=t_get18consts(ctime);

  % Phase relative to Greenwich (in units of cycles).
v=rem( const.doodson*astro+const.semi, 1);

  v=v(ju);
u=zeros(size(v));
f=ones(size(v));

else 

  [const,sat,shallow]=t_getconsts(ctime);

  % Phase relative to Greenwich (in units of cycles).
% (This only returns values when we have doodson#s, i.e., not for the 
% shallow water components, but these will be computed later.)
v=rem( const.doodson*astro+const.semi, 1);

  if nargin==4, % If we have a latitude, get nodal corrections.

    % Apparently the second-order terms in the tidal potential go to zero
% at the equator, but the third-order terms do not. Hence when trying
% to infer the third-order terms from the second-order terms, the 
% nodal correction factors blow up. In order to prevent this, it is 
% assumed that the equatorial forcing is due to second-order forcing 
% OFF the equator, from about the 5 degree location. Latitudes are 
% hence (somewhat arbitrarily) forced to be no closer than 5 deg to 
% the equator, as per note in Foreman.

    if isfinite(lat) & (abs(lat)<5); lat=sign(lat).*5; end

    slat=sin(pi.*lat./180);
% Satellite amplitude ratio adjustment for latitude. 

    rr=sat.amprat;           % no amplitude correction

    if isfinite(lat),
j=find(sat.ilatfac==1); % latitude correction for diurnal constituents
rr(j)=rr(j).*0.36309.*(1.0-5.0.*slat.*slat)./slat;

      j=find(sat.ilatfac==2); % latitude correction for semi-diurnal constituents
rr(j)=rr(j).*2.59808.*slat;
else 
rr(sat.ilatfac>0)=0;
end;

    % Calculate nodal amplitude and phase corrections.

    uu=rem( sat.deldood*astro(4:6)+sat.phcorr, 1);

    %%uu=uudbl-round(uudbl);  <_ I think this was wrong. The original
%                         FORTRAN code is:  IUU=UUDBL
%                                           UU=UUDBL-IUU
%                         which is truncation.        

% Sum up all of the satellite factors for all satellites.

    nsat=length(sat.iconst);
nfreq=length(const.isat);

    fsum=1+sum(sparse([1:nsat],sat.iconst,rr.*exp(i*2*pi*uu),nsat,nfreq)).';

    f=abs(fsum);
u=angle(fsum)./(2.*pi);

    % Compute amplitude and phase corrections for shallow water constituents. 

    for k=find(isfinite(const.ishallow))',
ik=const.ishallow(k)+[0:const.nshallow(k)-1];
f(k)=prod(f(shallow.iname(ik)).^abs(shallow.coef(ik)));
u(k)=sum( u(shallow.iname(ik)).*shallow.coef(ik) );
v(k)=sum( v(shallow.iname(ik)).*shallow.coef(ik) );
end;

    f=f(ju);
u=u(ju);
v=v(ju);

  else % Astronomical arguments only, so nodal corrections.

    % Compute phases for shallow water constituents.
for k=find(isfinite(const.ishallow))',
ik=const.ishallow(k)+[0:const.nshallow(k)-1];
v(k)=sum( v(shallow.iname(ik)).*shallow.coef(ik) );
end;
v=v(ju);
f=ones(size(v));
u=zeros(size(v));
end;
end;

%调用交点计算程序，获取交点因子、订正角、初相位，黄经

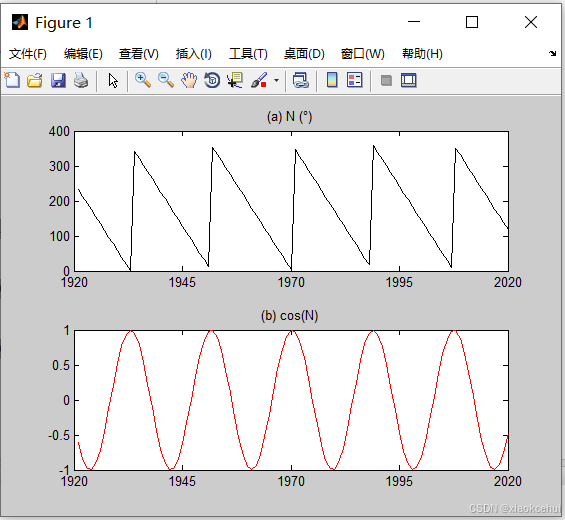
%绘制黄经N

[ff,uu,vv,N]=s_nodal_cal({'K1';'O1';'M2'},[1920,01,01],[2020,01,01],365,10);

subplot(2,1,1);plot(N,'k');hold on;

set(gca,'XTick',0:25:2020);title('(a) N (°)');

set(gca,'XTickLabel',{'1920','1945','1970','1995','2020'})

subplot(2,1,2);plot(cosd(N),'r');hold on;

set(gca,'XTick',0:25:2020);title('(b) cos(N)');

set(gca,'XTickLabel',{'1920','1945','1970','1995','2020'})

%计算交点因子、订正角、初相位和黄经
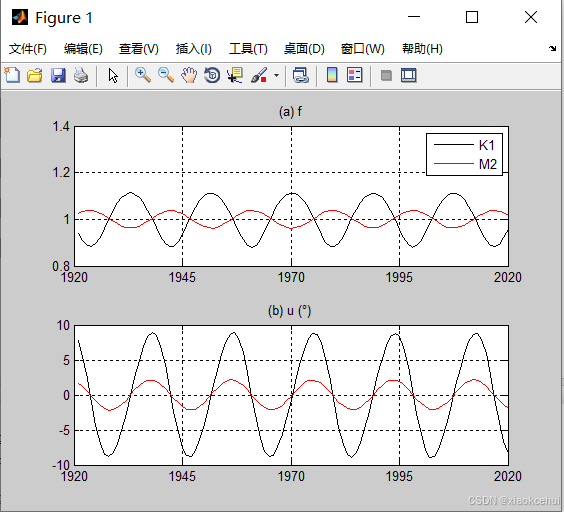
%绘制K1、M2分潮的交点因子、订正角

[ff,uu,vv,N]=s_nodal_cal({'K1';'M2'},[1920,01,01],[2020,01,01],365,10);

subplot(2,1,1);plot(ff(1,:),'k');hold on;plot(ff(2,:),'r');grid on;

legend('K1','M2');set(gca,'XTick',0:25:2020)

set(gca,'XTickLabel',{'1920','1945','1970','1995','2020'})

title('(a) f')

subplot(2,1,2);plot(uu(1,:),'k');hold on;plot(uu(2,:),'r');grid on;

set(gca,'XTick',0:25:2020)

set(gca,'XTickLabel',{'1920','1945','1970','1995','2020'})

title('(b) u (°)')

作为非专业人士，理解到t_vuf已经是博主的极限了。如果看t_vuf函数内部的内容，根本搞不懂。

t_vuf函数还用到2个函数t_getconsts和 t_astron，就粘贴函数代码了，只看看它们的描述。

% t_astron函数

计算儒略日JD时刻（世界协调时UTC，具体详见代码说明）的天文参数 A = [τ, s, h, p, np, pp]（单位：周角）及其时间变化率

function [astro,ader] = t_astron(jd)
% T_ASTRON Computes astronomical Variables
% [A,ADER] = ASTRON(JD) computes the astronomical variables 
%            A=[tau,s,h,p,np,pp] (cycles) 
%  and their time derivatives 
%            ADER=[dtau,ds,dh,dp,dnp,dpp] (cycles/day) 
%  at the matlab time JD (UTC, but see code for details) where
%
%    tau = lunar time
%    s = mean longitude of the moon
%    h = mean longitude of the sun
%    p = mean longitude of the lunar perigee 
%    np = negative of the longitude of the mean ascending node
%    pp = mean longitude of the perihelion (solar perigee)   
%

%
%    The formulae for calculating these ephemerides (other than tau) 
%    were taken from pages 98 and 107 of the Explanatory Supplement to
%    the Astronomical Ephemeris and the American Ephemeris and Nautical 
%    Almanac (1961). They require EPHEMERIS TIME (ET), now TERRESTRIAL 
%    TIME (TT) and are based on observations made in the 1700/1800s.
%    In a bizarre twist, the current definition of time is derived
%    by reducing observations of planetary motions using these formulas.
%
%    The current world master clock is INTERNATIONAL ATOMIC TIME (TAI).
%    The length of the second is based on inverting the actual 
%    locations of the planets over the period 1956-65 into "time" 
%    using these formulas, and an offset added to keep the scale 
%    continuous with previous defns. Thus
%
%                     TT = TAI + 32.184 seconds.
%
%    Universal Time UT is a time scale that is 00:00 at midnight (i.e.,
%    based on the earth's rotation rather than on planetary motions).
%    Coordinated Universal Time (UTC) is kept by atomic clocks, the 
%    length of the second is the same as for TAI but leap seconds are
%    inserted at intervals so that it provides UT to within 1 second. 
%    This is necessary because the period of the earth's rotation is 
%    slowly increasing (the day was exactly 86400 seconds around 1820, 
%    it is now about 2 ms longer). 22 leap seconds have been added in 
%    the last 27 years.
%
%    As of 1/1/99,    TAI = UTC + 32 seconds.
%       
%    Thus,             TT = UTC + 62.184 seconds
%
%    GPS time was synchronized with UTC 6/1/1980 ( = TAI - 19 secs), 
%    but is NOT adjusted for leap seconds. Your receiver might do this
%    automatically...or it might not.
%
%    Does any of this matter? The moon longitude is the fastest changing
%    parameter at 13 deg/day. A time error of one minute implies a
%    position error of less than 0.01 deg. This would almost always be 
%    unimportant for tidal work.
%
%    The lunar time (tau) calculation requires UT as a base.  UTC is 
%    close enough - an error of 1 second, the biggest difference that
%    can occur between UT and UTC, implies a Greenwich phase error of 
%    0.01 deg.  In Doodson's definition (Proc R. Soc. A, vol 100, 
%    reprinted in International Hydrographic Review, Appendix to 
%    Circular Letter 4-H, 1954) mean lunar time is taken to begin at 
%    "lunar midnight". 
% T_ASTRON 计算天文参数
% [A, ADER] = ASTRON(JD) 计算儒略日JD时刻（世界协调时UTC，具体详见代码说明）的
% 天文参数 A = [τ, s, h, p, np, pp]（单位：周角）
%及其时间变化率
% ADER = [dτ, ds, dh, dp, dnp, dpp]（单位：周角/天）
% 其中：
% τ = 月球时角
% s = 月球平经度
% h = 太阳平经度
% p = 月球近地点平经度
% np = 月球升交点平经度的负值
% pp = 近日点平经度（太阳近地点）

%
% 这些星历参数（除τ外）的计算公式源自《天文星历解释性补充说明及
% 美国星历与航海年历》（1961年）第98和107页，需采用历书时（ET）
% ——现称为地球时（TT）——作为时间基准，其观测数据基于18-19世纪的记录。
% 耐人寻味的是，当前时间标准的定义正是通过使用这些公式
% 对行星运动观测数据进行归算而推导得出的。
%
% 当前世界主钟采用国际原子时（TAI），其秒长定义基于1956-65年间
% 通过上述公式对行星实际位置反算推导的"时间"尺度，
% 并通过添加偏移量保持与历史时间定义的连续性。因此：
%
% TT = TAI + 32.184 秒
%
% 世界时（UT）是以午夜零时为起点的时标（基于地球自转而非行星运动）。
% 协调世界时（UTC）由原子钟守时，其秒长与TAI相同，但通过间隔插入闰秒
% 使其与UT的偏差保持在1秒以内。此举的必要性在于地球自转周期
% 正逐渐变长（1820年时1日恰好为86400秒，现今已延长约2毫秒）。
% 过去27年间已添加22次闰秒。
%
% 截至1999年1月1日：TAI = UTC + 32 秒
%
% 因此： TT = UTC + 62.184 秒
%
% GPS时在1980年6月1日与UTC同步（= TAI - 19秒），但不进行闰秒调整。
% 用户接收设备可能自动实现闰秒补偿...亦可能未作处理。
%
% 这些时差影响几何？月球经度变化最快达13度/天。1分钟的时间误差
% 导致的定位偏差小于0.01度，对潮汐研究通常可忽略不计。
%
% 月球时角（τ）计算需以UT为基准。UTC已足够近似——UT与UTC之间
% 最大可能存在的1秒误差，对应的格林尼治相位误差仅为0.01度。
% 根据杜德森定义（《皇家学会会刊A辑》第100卷，1954年转载于
% 《国际水文评论》4-H号通函附录），平月球时以"月球午夜"为起始点。

% t_getconsts函数

主要读取t_constituents.mat文件

获取分潮数据结构，返回包含潮汐分析信息的数据结构

function [const,sat,shallow]=t_getconsts(ctime);
% T_GETCONSTS Gets constituent data structures
% [CONST,SAT,SHALLOW]=T_GETCONSTS returns data structures holding
% information for tidal analyses.
%
% Variables are loaded from 't_constituents.mat', otherwise the 
% ascii files 'tide3.dat' (provided with the IOS analysis package)
% and 't_equilib.dat' are read, and the results stored in 
% 't_constituents.mat' for future use.
%
% [...]=T_GETCONSTS(TIME) recomputes the frequencies from the 
% rates-of-change of astronomical parameters at the matlab TIME given.
% T_GETCONSTS 获取分潮数据结构
% [CONST,SAT,SHALLOW]=T_GETCONSTS 返回包含潮汐分析信息的数据结构
%
% 程序优先从't_constituents.mat'文件加载变量，若该文件不存在，
% 则读取IOS潮汐分析包提供的ASCII文件'tide3.dat'及't_equilib.dat'，
% 并将处理结果保存至't_constituents.mat'供后续使用
%
% [...]=T_GETCONSTS(TIME) 根据给定的MATLAB时间TIME，
% 通过天文参数变化率重新计算频率

t_constituents.mat文件的结构体字段进行了翻译。

t_constituents.mat

 const=struct('name',setstr(zeros(nc,4)),... % constituent names
'freq',empvec,...              % and frequencies (cph)
'kmpr',setstr(zeros(nc,4)),... % names of comparisons
'ikmpr',empvec,'df',empvec,... % ..and their index (into .name)
'doodson',zeros(nc,6)+NaN,...  % doodson#s (when available)
'semi',empvec,...              % phase offsets
'isat',empvec,...              % index into "sat"
'nsat',empvec,...              % # of associated satellites in "sat"
'ishallow',empvec,...          % index in "shallow"
'nshallow',empvec,...          % # of generating freqs in "shallow"
'doodsonamp',empvec,...        % Equilibrium Amplitude (when available)
'doodsonspecies',empvec);      % Species
nsat=162;
sat=struct('deldood',zeros(nsat,3),...  % changes in last 3 doodson#s 
'phcorr',zeros(nsat,1),...   % phase corrections
'amprat',zeros(nsat,1),...   % amplitude corrections
'ilatfac',zeros(nsat,1),...  % latitude-dependent correction type
'iconst',zeros(nsat,1));     % index of major (in const.)

nshl=251;
shallow=struct('iconst',zeros(nshl,1),... % index of shallow constituent name
'coef',zeros(nshl,1),...   % corresponding combination number and
'iname',zeros(nshl,1));    % index of main constituent

const=struct('name',setstr(zeros(nc,4)),... % 分潮名称'freq',empvec,...              % 频率（单位：周/小时）'kmpr',setstr(zeros(nc,4)),... % 比较项名称'ikmpr',empvec,'df',empvec,... % 及其索引（指向.name字段）'doodson',zeros(nc,6)+NaN,...  % 杜德森数（若可用）'semi',empvec,...              % 相位偏移量'isat',empvec,...              % 指向"sat"结构的索引'nsat',empvec,...              % "sat"中关联卫星分潮的数量'ishallow',empvec,...          % 指向"shallow"结构的索引'nshallow',empvec,...          % "shallow"中生成频率的数量'doodsonamp',empvec,...        % 平衡潮振幅（若可用）'doodsonspecies',empvec);      % 种类nsat=162;sat=struct('deldood',zeros(nsat,3),...  % 最后3个杜德森数的变化量'phcorr',zeros(nsat,1),...   % 相位校正值'amprat',zeros(nsat,1),...   % 振幅校正系数'ilatfac',zeros(nsat,1),...  % 纬度相关校正类型'iconst',zeros(nsat,1));     % 主分潮索引（指向const结构）nshl=251;shallow=struct('iconst',zeros(nshl,1),... % 浅水分潮名称的索引'coef',zeros(nshl,1),...   % 相应的组合数和'iname',zeros(nshl,1));    % 主分潮的索引