Codeforces Round 1033 (Div. 2) and CodeNite 2025 vp补题
烂
原题连接
A 模拟
搬砖题
每条边两种情况 要么都相等,要么小的两条相加等于大的
(一开始没有注意到三个矩形的大小关系 卡了很长时间…
B 找规律
- 在这三个矩形线上的球不会进袋,会一直转
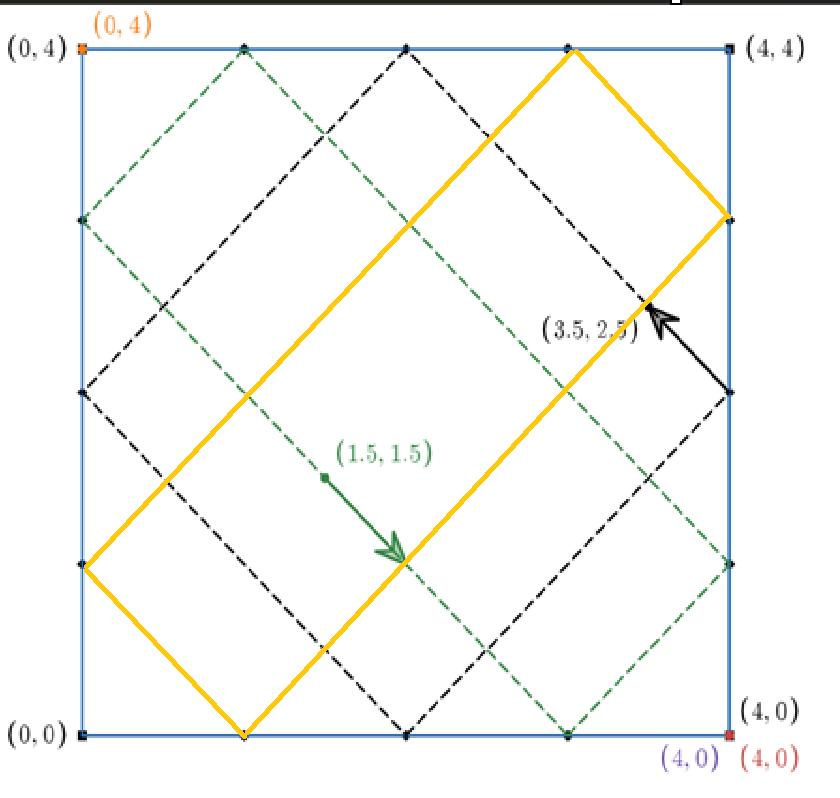
只有在对角线上的球能进 - 球之间会发生碰撞
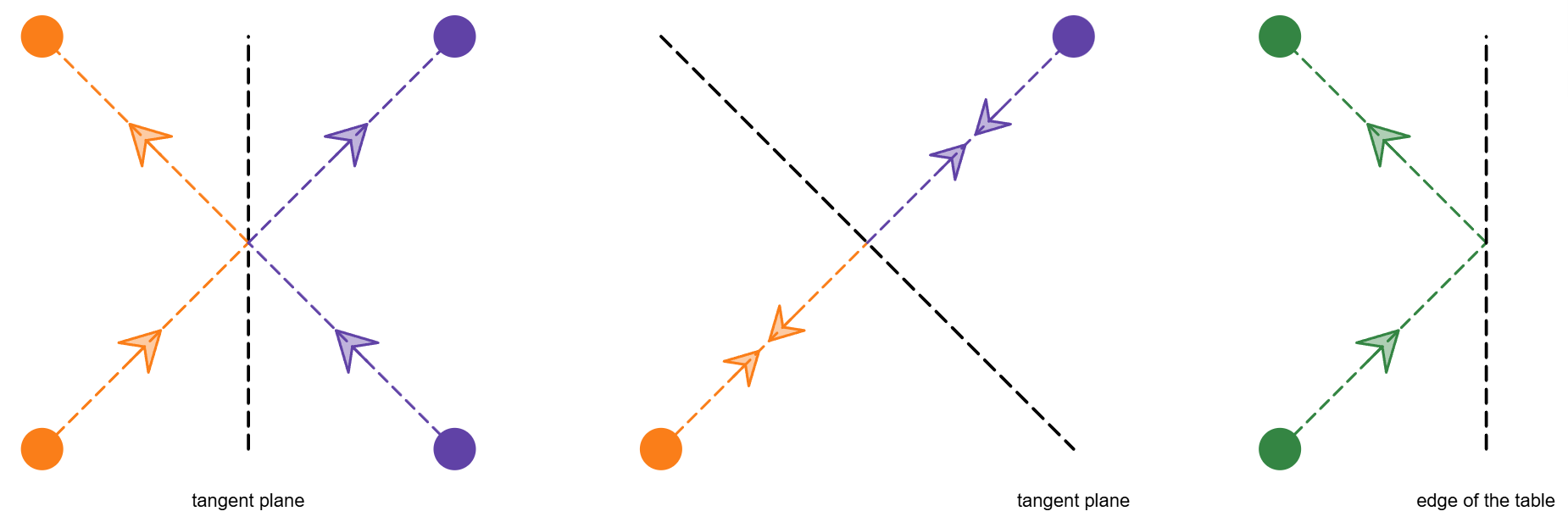
但是同一轨迹的相撞不变轨迹
垂直轨迹的相撞极限一换一,也相当于轨迹不变
void solve(){int n,s;cin>>n>>s;int ans=0;forr(i,1,n){int dx,dy,x,y;cin>>dx>>dy>>x>>y;if(x+y==s&&dx*dy<0)ans++;else if(x==y&&dx*dy>0)ans++;}cout<<ans<<endl;
}
C 思维
读假题了 以为不会算根的d(v)值…
- 先判定合法 树的两种极端结构——
- 链(除了根,其他d(v)=1,summin=i+n−1sum_{min}=i+n-1summin=i+n−1)
- 菊花图(d(v)=min(root,v),summax=i(i+1)2+i(n−i)sum_{max}=\frac{i(i+1)}{2}+i(n-i)summax=2i(i+1)+i(n−i)
- 之后问题在于怎么分m
一个dalao的做法:分配m
void solve(){int n,m;cin>>n>>m;vector<int>a(n+1,0);if(!(m>=n&&m<=n*(n+1)/2))return cout<<"-1\n",void();int id=0,dt=m;//分配mforr(i,1,n){if(dt>n-i+1)dt-=(n-i+1),a[++id]=i;//后面数都能分到ielse{//不够分 剩了dt个1分给n-dt+1~n i~n-dt不分forr(j,i,n-dt)a[++id]=i-1;//能分到上一个 i-1forr(j,n-dt+1,n)a[++id]=i;break;}}//a[]数组非递减//d(root)=root,最大的是根,没有其他小的数覆盖int pre=a[n],nxt=a[n]+1;//nxt是被root覆盖的点cout<<a[n]<<endl;reforr(i,1,n-1){if(a[i]==a[i+1])cout<<pre<<' '<<(pre=nxt++)<<endl;//如果相等 说明有大的数被覆盖了 小的连接大的else cout<<pre<<' '<<(pre=a[i])<<endl;//不相等 连续的 没有大的数被覆盖}
}
另一个dalao的做法
从菊花图summaxsum_{max}summax开始向m凑
大的点合并到小的点可以让sum变小
void solve()
{int n,m;cin>>n>>m;int rt=-1;forr(i,1,n){int low=i+n-1,up=i*(i+1)/2+(n-i)*i;if(low<=m&&m<=up){rt=i;break;}}if(rt==-1)return cout<<-1<<endl,void();int dis=rt*(rt+1)/2+(n-rt)*rt-m;vector<int>fa(n+1,rt);//菊花图reforr(i,1,n){if(dis==0)break;int d=min(i,rt);//当前的d(v)//d(v)-1是减掉最大的if(dis>=d-1){//移到1下面dis-=(d-1);fa[i]=1;}else{//dis<d-1int aim=d-dis;fa[i]=aim;break;}}cout<<rt<<endl;forr(i,1,n){if(i!=rt)cout<<fa[i]<<' '<<i<<endl;}
}
D 组合数学 鸽巢原理
题意:对任意n∗mn*mn∗m,每个数[1,k]的矩阵,能找到a∗ba*ba∗b相同的数组成的子矩阵,找字典序最小的(n,m)
首先让n最小,重复k个数比重复k个数的组合的种数要少
所以先考虑对单列,k+1k+1k+1行会重复一个数,需要a行重复的,n=(a−1)k+1n=(a-1)k+1n=(a−1)k+1
对每行,设每列有x种组合m=(b−1)x+1m=(b-1)x+1m=(b−1)x+1
这x种要满足之前每列有a个重复的,xmax=k⋅Cnax_{max}=k\cdot C_n^axmax=k⋅Cna,就是n个数中选a个相同,相同的数有k种情况
int qpow(int x,int a){int res=1;while (a){if(a&1)res=res*x%mod;x=x*x%mod;a>>=1;}return res%mod;
}
int inv(int x){return qpow(x,mod-2)%mod;
}
int C(int n,int a){int res=1,tp=1;forr(i,1,a){tp=tp*i%mod;}forr(i,n-a+1,n){res=res*i%mod;}return res*inv(tp)%mod;
}
void solve(){int a,b,k;cin>>a>>b>>k;int n=((a-1)*k+1)%mod;int m=(k*C(n,a)%mod*(b-1)%mod+1)%mod;cout<<n<<' '<<m<<endl;
}
