优选算法:二分查找
二分查找算法是查询算法一种,一般在有序数组中进行查询,时间复杂度是O(logn),但是在无序数组中寻找到一些规律也可以使用二分。二分查找是有模板的,因此一些题就可以在模版基础上修改即可,但是也有些题需要具体分析才能使用。
模版有三个:最朴素的二分查找模版,寻找左边的边界的二分查找模版,寻找右边的查找模版。
具体实现:
二分查找
题目描述
算法思路
二分查找的最主要核心是二段性,可以通过一些手段将数组分为两段区间,根据区间来寻找到目标数。这道题中数组是有序的同时是在数组中寻找数,因此我们就可以通过二分进行处理。目标数是tar,我们可以根据数组是有序的进行二分,找到中间点mid,将数组分为两段,此时就会看到mid的右边全是大于mid,左边就全是小于它的,那么我们将mid和tar进行对比,如果mid大于tra,那么如果tra存在,就一定在mid的左边,反之右边。此时就可以将right进行更新,再对新的区间进行二分查找。这题就是二分查找最简单的使用。
算法实现
public int search(int[] nums, int target) {int left = 0;int right = nums.length-1;while(left<=right){int mid = (left+right)/2;if(nums[mid]>target){right = mid-1;}else if(nums[mid]<target){left=mid+1;}else{return mid;}}return -1;}朴素二分的模版
while(left<=right){
int mid = left + (right-left) / 2;或者left+(right - left+1)/2;
if(....) left= mid + 1;
else if(....) right = mid+1;
else return ...;}其中的省略号是要根据不同的题目进行修改的。
在排序数组中寻找第一和最后一个位置
题目描述
 算法思路
算法思路
这道题就体现了二分查找的寻找左端点和右端点。这道题中数组是非递减的,数组中要不就是上升要不就是不变,又是要根据二段性寻找目标数,此时就使用二分查找。首先是寻找左端点tra,我们可以发现,数组可以分为两段,一段是小于tra的,一段是大于等于tra的,那么我们根据二分查找到的点mid如果落到左边,此时我们就更新left让left=mid+1;当mid落到左边,此时就可以将right更新,但是我们不可以让right=mid-1,当mid落到最左端端点时,mid-1就会跳过目标值,因此只能让right=mid。
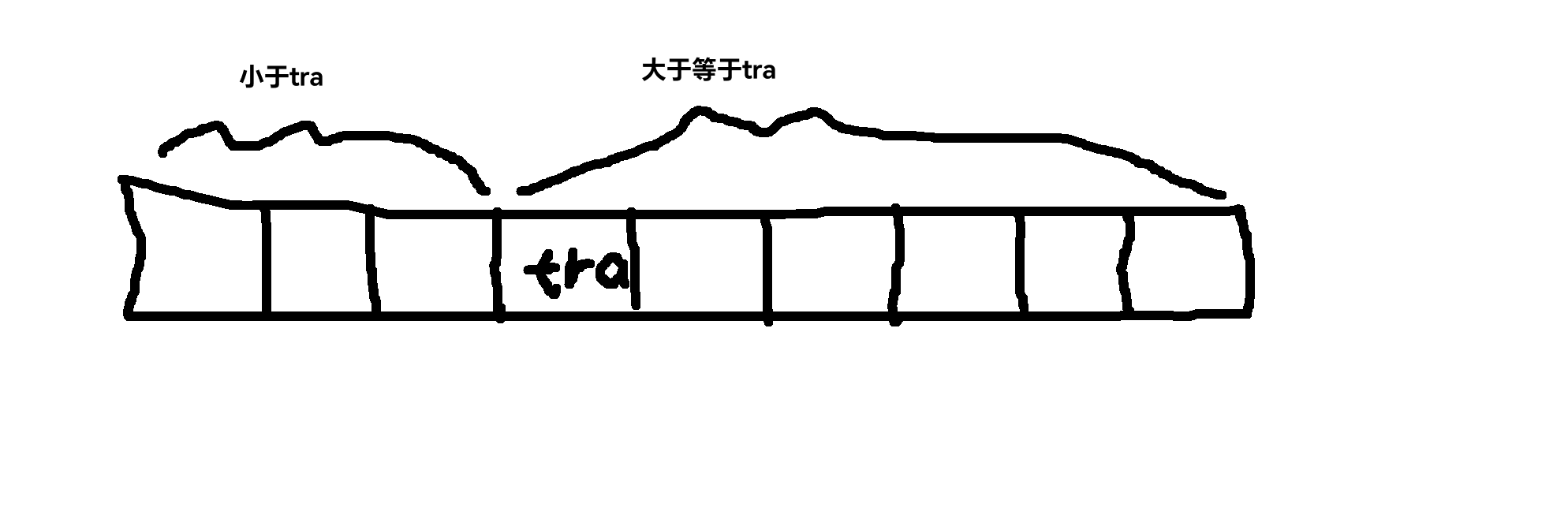
查找右端点,右端点也可以根据二段性分为两段,一段是小于等于,一段是大于tra,此时我们也是要注意上面的越界情况。
细节处理
在朴素模板中我们使用的是left<=right,但是我们发现当进行最后一次二分的时候,就已经判断完成left==right,那么此时就不用再次判断left等于right的情况了,如果判断就会死循环。
这里的寻找左端点的mid的操作是能加一的,而右端点的是不能加一的。
算法实现
public int[] searchRange(int[] nums, int target) {int[] arr = new int[2];arr[0] = arr[1] = -1;if(nums.length == 0) return arr;if(nums.length==1&&nums[0]==target){arr[0] = arr[1] = 0;return arr;}int left = 0;int right = nums.length-1;//找到左端顶while(left<right){int mid = left + (right - left)/2;if(nums[mid]<target){left = mid+1;}else{right = mid;}}if(nums[left] != target) return arr;else arr[0] = left;left = 0;right = nums.length - 1;//右端点while(left<right){int mid = left + (right - left + 1 )/2;if(nums[mid]>target){right = mid-1;}else{left = mid;}} if(nums[left]==target)arr[1] = right;else return arr;return arr;}二分查找寻找左/右端点
左端点
while(left<right){
int mid = left + (right-left) / 2;
if(....) left= mid + 1;
else if(....) right = mid;
else return ...;
}右端点
while(left<right){
或者left+(right - left+1)/2;
if(....) left= mid;
else if(....) right = mid-1;
else return ...;}这里的mid求值其实可以看上面有加一,下面就减一。
搜索插入位置
算法思路
这题根据题意就能知道使用二分。我们根据二分区间,大于和小于等于,直接套用二分模版。唯一注意就是当大于数组最后一个值时,此时就返回最后一个下标加一。
算法实现
public int searchInsert(int[] nums, int target) {int left = 0;int right = nums.length - 1;while(left<right){int mid = left+(right - left) /2;if(nums[mid]<target){left = mid+1;}else{right = mid;}}if(nums[left]<target) {return left+1;}elsereturn left;}X的平方根
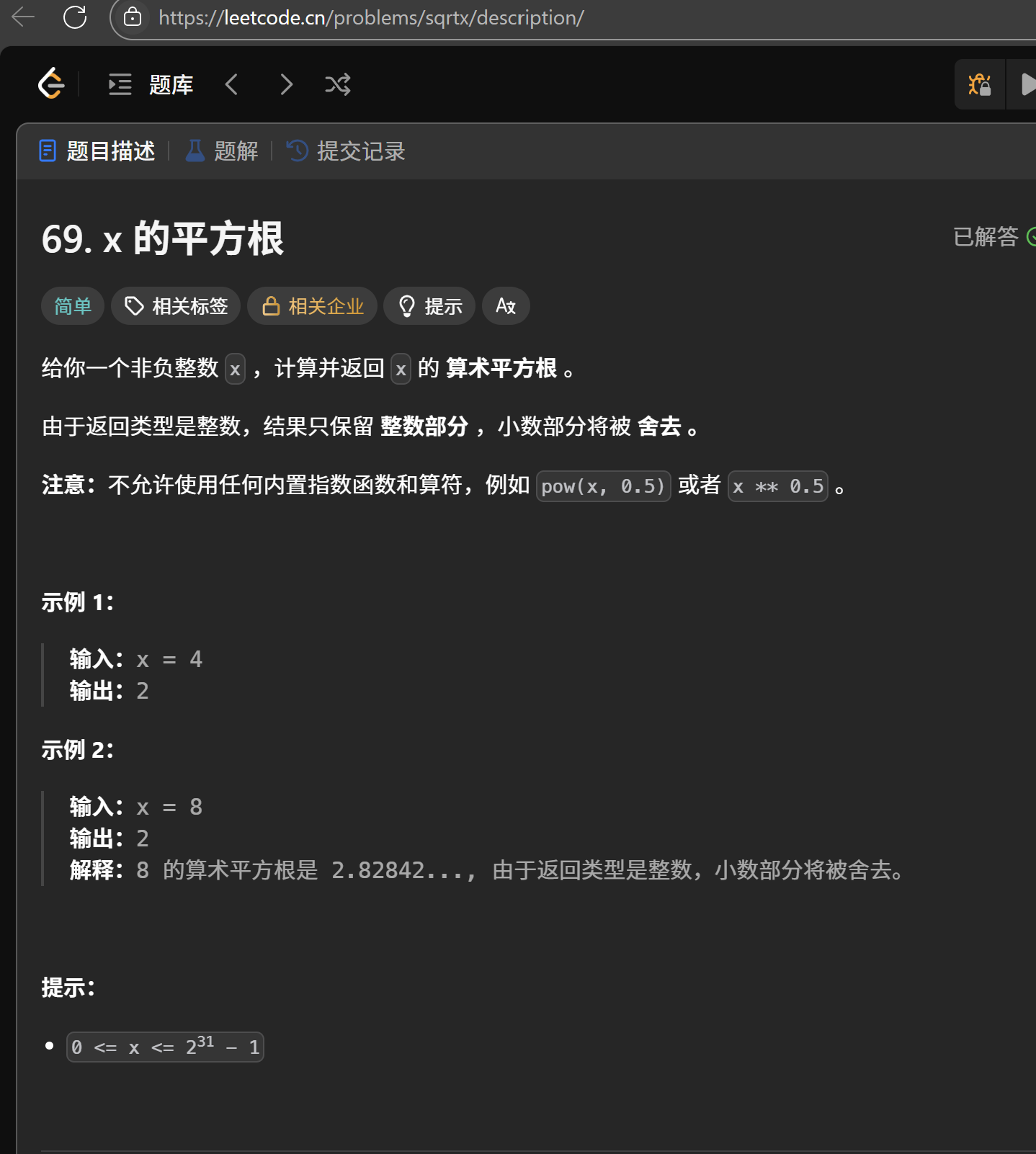
算法思路
我们可以发现x的算术平方根其实是在0~x之间的,那么就可以将问题转换成在0~x之间寻找目标值tra。那门就可以根据二分进行查找,当mid的平方后大于x,此时就让right=mid-1,反之让left=mid。
算法实现
public int mySqrt(int x) {long left = 0;long right = x;while(left<right){long mid = left + (right - left+1) / 2;if(mid*mid<=x){left = mid;}else{right = mid-1;}}return (int)left;}山峰数组山顶索引
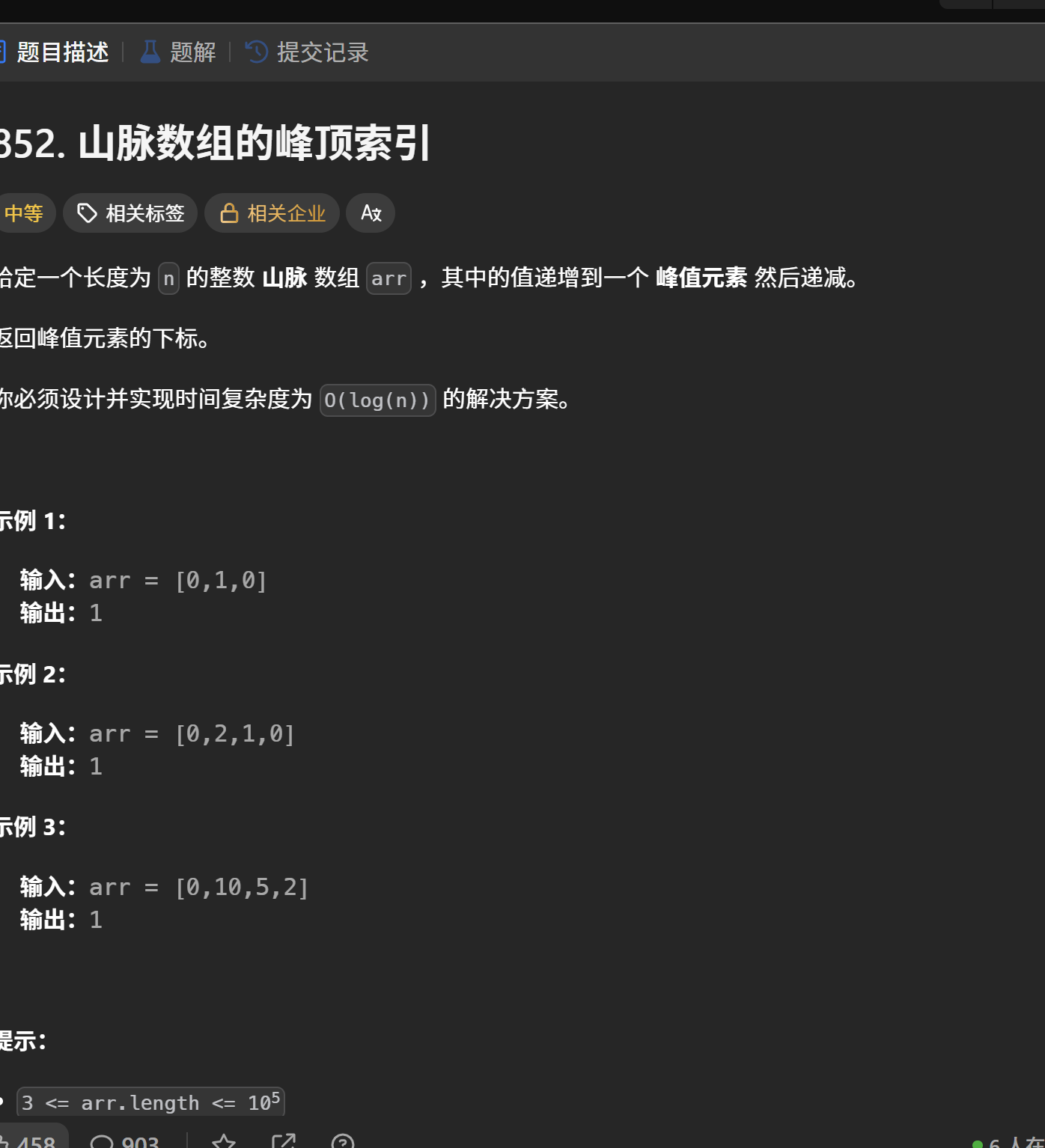
算法思路
这道题中我们通过二分找到mid,会有两种情况,一是mid的值大于mid-1,大于的情况有两种:一是mid等于峰值,二是在递增区间上,所以只我们就需要将left区间更新,因为mid可能等于峰值,所以只能更新到left=mid;第二种情况是mid小于等于mid-1的值,只有一种情况就是处于递减区间,因此我们要减少right的范围。
算法实现
public int peakIndexInMountainArray(int[] arr) {int left = 0; int right = arr.length;while(left<right){int mid = left + (right-left+1)/2;if(arr[mid]>arr[mid-1]){left = mid;}else{right = mid-1;}}return left;}寻找旋转数组的最小值
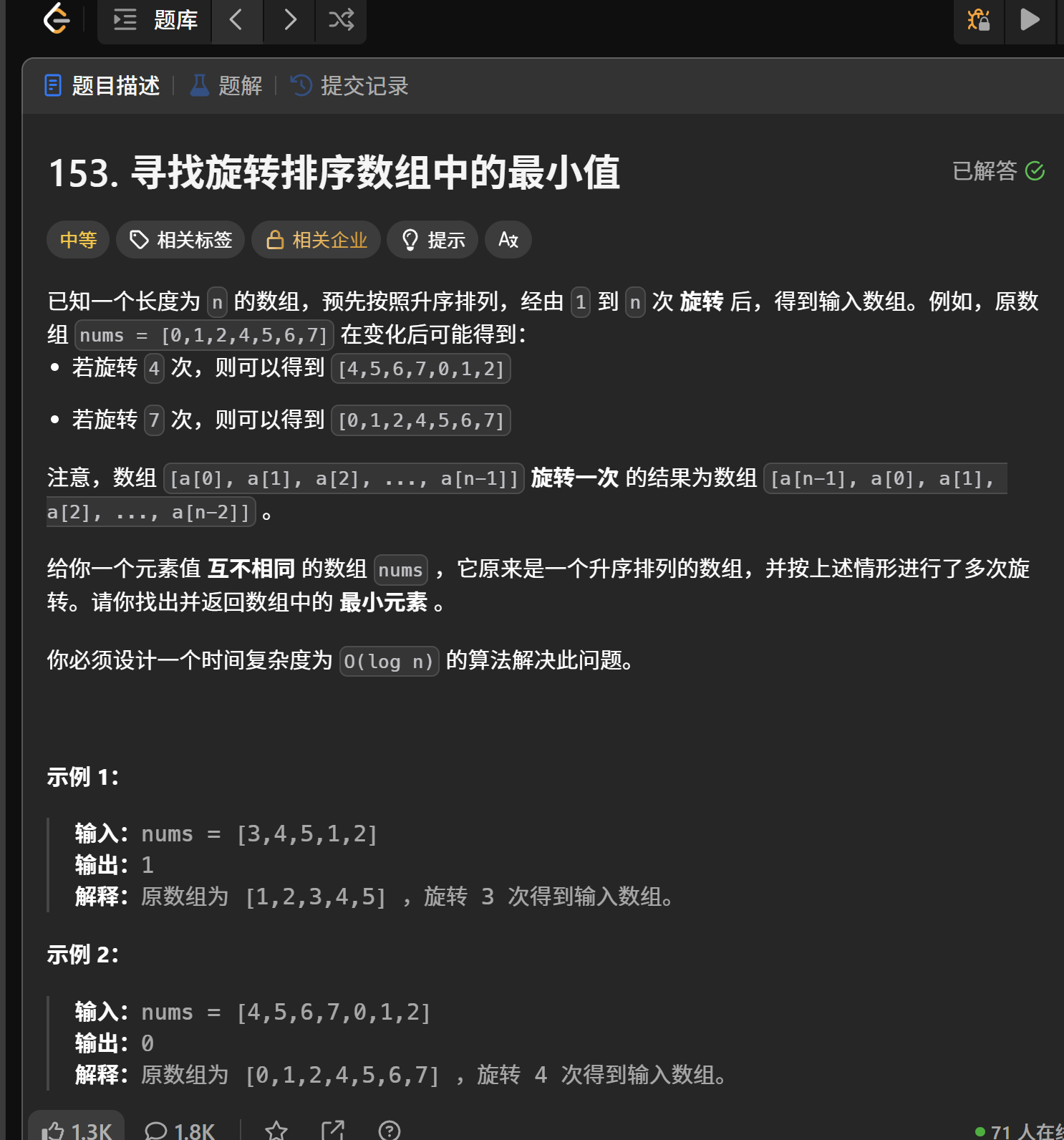
算法思路
这里我们可以将数组想象成一段线段:
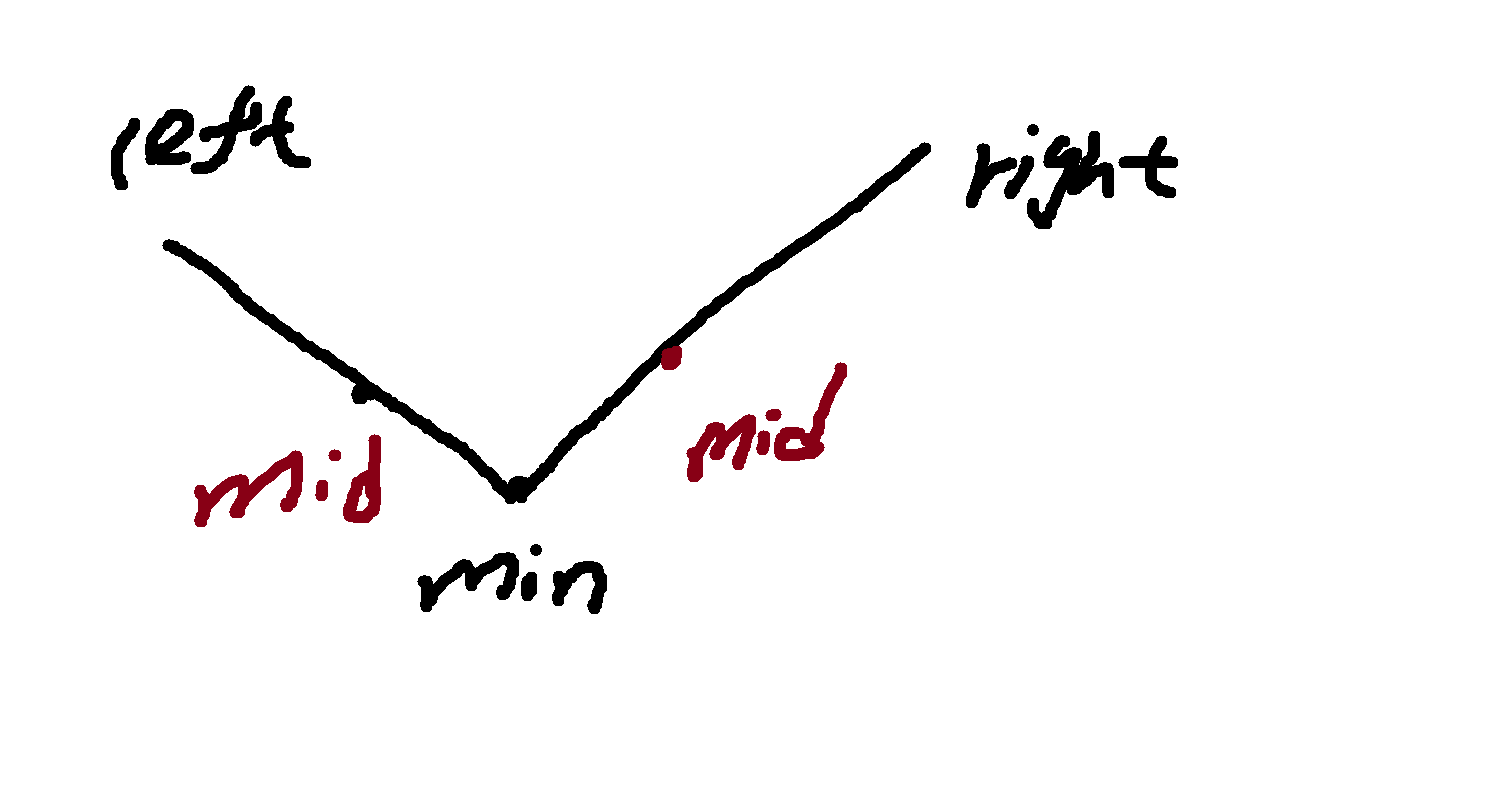
当mid小于right时,此时mid可能在递增区间,也可能在min出,所以们更新right=mid;第二种情况就是大于rght,肯定是大于min,此时更新left=mid+1。
算法实现
public int findMin(int[] nums) {int left = 0; int right = nums.length-1;int x = nums[right];while(left<right){int mid = left+(right-left)/2;if(nums[mid]<=x){right=mid;}else{left= mid+1;}}return nums[left];}