北方苍鹰优化算法优化的最小二乘支持向量机NGO-LSSVM多输入多输出回归预测【MATLAB】
在复杂的工程与科学应用中,我们常常面临需要同时预测多个目标变量的挑战,例如,根据气象数据同时预测温度、湿度和风速,或根据工业参数同时预测产品质量的多个指标。这类“多输入多输出”(MIMO)的回归预测任务对模型的泛化能力和精度提出了更高要求。本文将介绍一种结合了新型智能优化算法与经典机器学习模型的创新方法——由北方苍鹰优化算法(Northern Goshawk Optimization, NGO)优化的最小二乘支持向量机(Least Squares Support Vector Machine, LSSVM),并展示其在MATLAB中的实现与应用。
为什么需要智能优化与LSSVM结合?
最小二乘支持向量机(LSSVM)是支持向量机(SVM)的一种高效变体,它通过将不等式约束转化为等式约束,简化了求解过程,特别适合处理回归问题。LSSVM具有强大的非线性拟合能力和良好的泛化性能,但其预测效果高度依赖于两个关键参数的选择:正则化参数和核函数参数。传统的人工试错或网格搜索方法效率低下,且难以找到全局最优解。
为了解决这一难题,我们引入了北方苍鹰优化算法(NGO)。NGO是一种受自然界中北方苍鹰捕猎行为启发而提出的新型元启发式智能优化算法。它模拟了苍鹰在搜寻猎物时的探索、围攻和精准打击策略,具备出色的全局搜索能力和快速收敛特性。将NGO应用于LSSVM的参数寻优过程,能够自动、高效地寻找使模型预测性能最佳的参数组合,从而显著提升模型的整体表现。
模型核心思想与工作流程
该方法的核心思想是:利用北方苍鹰优化算法的“智慧”来为最小二乘支持向量机“配置最佳装备”,使其在面对复杂多输出预测任务时发挥最大潜力。
-
问题定义与数据准备:
首先,明确预测目标,收集并整理包含多个输入变量和多个输出变量的历史数据集。对数据进行必要的预处理,如缺失值处理、异常值剔除和归一化,以确保数据质量。 -
构建LSSVM基础模型:
在MATLAB中,利用LSSVM工具箱或相关函数搭建多输出LSSVM模型框架。此时,模型的参数处于待定状态。 -
NGO驱动的参数优化:
- 初始化:将LSSVM的待优化参数(正则化参数和核参数)编码为“猎物”的位置,随机生成一群“北方苍鹰”(即候选解)。
- 迭代寻优:在每一次迭代中,每只“苍鹰”根据当前“猎物”(参数组合)的位置和群体经验,更新自己的位置(即调整参数值)。
- 性能评估:使用当前参数组合训练LSSVM模型,并在验证集上计算预测误差(如均方根误差RMSE或平均绝对误差MAE)。该误差值作为“猎物”的“价值”,指导“苍鹰”们的搜索方向。
- 更新与收敛:重复上述过程,群体不断向更优的“猎物”位置聚集,直至达到预设的迭代次数或收敛条件。最终,找到使预测误差最小的最优参数组合。
-
模型训练与预测:
使用NGO寻找到的最优参数,重新训练最终的LSSVM模型。训练完成后,模型即可用于新的多输入数据,同时输出多个预测结果。
MATLAB实现关键步骤
在MATLAB环境中实现该方法,主要涉及以下几个环节:
- 数据加载与预处理:使用
xlsread、mapminmax等函数处理数据。 - LSSVM模型搭建:调用LSSVM相关的函数或编写核心求解代码,构建支持多输出的回归模型。
- NGO算法实现:编写NGO算法的核心函数,包括种群初始化、位置更新、适应度评估(即调用LSSVM进行训练和验证并返回误差)等。
- 主循环集成:将NGO优化器与LSSVM模型连接,让优化器不断为LSSVM提供新的参数组合,并接收误差反馈。
- 结果可视化:利用
plot、figure、xlim等函数,绘制预测值与真实值的对比图、误差分布图以及NGO的收敛曲线,直观展示模型性能。
应用场景与优势
该方法特别适用于:
- 环境科学:同时预测多种污染物浓度。
- 能源领域:预测电力系统中多个节点的负荷或电压。
- 智能制造:根据加工参数预测产品的多个质量指标。
- 金融分析:预测多个相关资产的价格走势。
其主要优势包括:
- 高预测精度:NGO的全局优化能力确保了LSSVM使用最优参数,显著提升多输出预测的准确性。
- 自动化程度高:摆脱了人工调参的繁琐,整个优化过程自动完成。
- 鲁棒性强:NGO算法对初始值不敏感,能稳定地找到高质量解。
- 适用性广:框架灵活,可轻松适配不同的数据集和预测需求。
结语
北方苍鹰优化算法(NGO)与最小二乘支持向量机(LSSVM)的结合,为多输入多输出回归预测提供了一种强大而智能的解决方案。通过MATLAB平台,这一先进的混合模型得以高效实现和验证。它不仅展现了生物启发式算法在机器学习领域的巨大潜力,也为解决复杂的现实世界预测问题开辟了新的途径。随着智能优化算法的持续发展,我们期待看到更多类似创新方法的涌现,推动预测技术迈向新的高度。
部分代码
%% 清空工作空间和环境
warning off; % 关闭警告提示
close all; % 关闭所有已打开的图形窗口
clear; % 清除工作区变量
clc; % 清空命令行窗口
rng('default')%% 添加 LSSVM 工具箱路径
addpath('LSSVM_ToolBox\'); % 确保工具箱函数可用%% 导入数据
res = xlsread('数据集.xlsx'); % 读取Excel数据(假设无标题行)%% 数据预处理与划分
num_size = 0.7; % 训练集占比 70%
outdim = 2; % 最后两列为输出变量
num_samples = size(res, 1); % 总样本数
res = res(randperm(num_samples), :); % 随机打乱数据顺序(可注释此行以禁用打乱)
num_train_s = round(num_size * num_samples); % 训练样本数量
f_ = size(res, 2) - outdim; % 输入特征维度% 划分输入输出:转置为【特征×样本】格式(符合神经网络习惯)
P_train = res(1:num_train_s, 1:f_)'; % 训练输入
T_train = res(1:num_train_s, f_+1:end)'; % 训练输出
P_test = res(num_train_s+1:end, 1:f_)'; % 测试输入
T_test = res(num_train_s+1:end, f_+1:end)'; % 测试输出M = size(P_train, 2); % 训练样本数
N = size(P_test, 2); % 测试样本数
运行结果
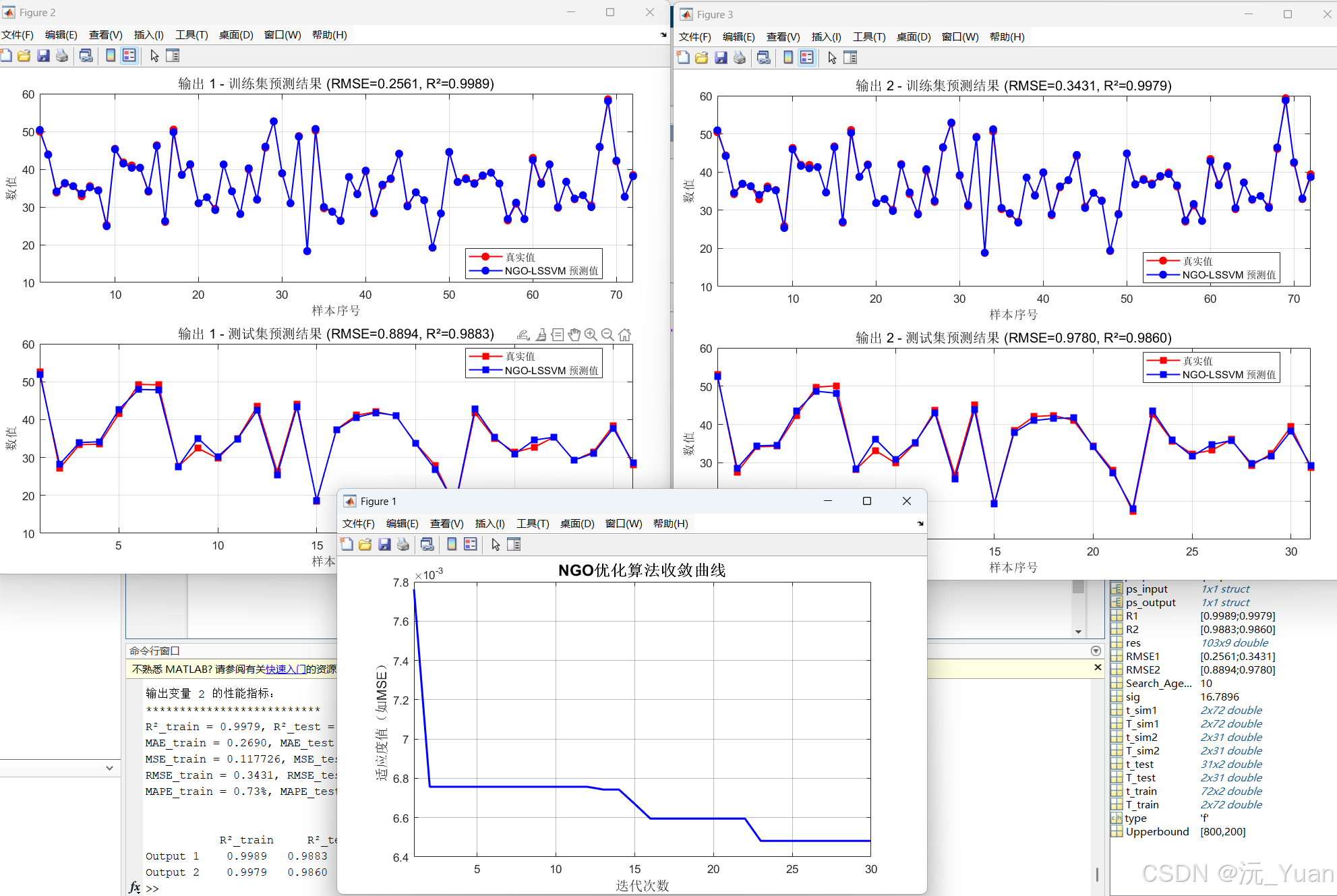
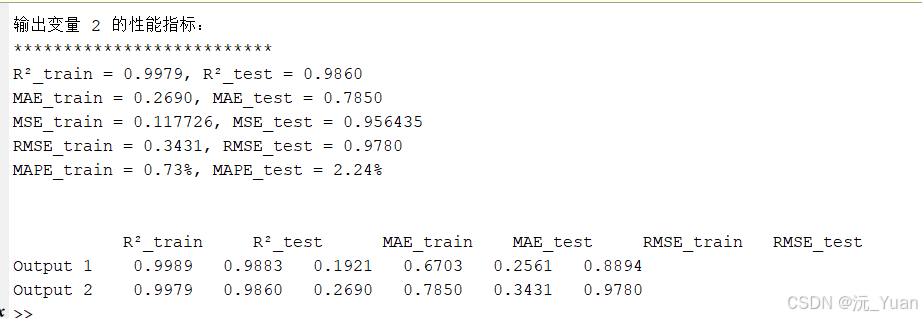
代码下载
https://mbd.pub/o/bread/YZWXk5ZyZQ==
