【机器学习入门】3.3 FP树算法——高效挖掘频繁项集的“树状神器”
在关联分析中,我们的核心目标是 “从海量事务数据中找频繁项集”(比如 “面包 + 牛奶”“尿布 + 啤酒” 这类经常一起出现的商品组合)。但早期的 Apriori 算法需要 “反复扫描数据”,面对万级、十万级数据时效率极低 —— 这时候,FP 树算法(FP-Tree Algorithm) 应运而生。
FP 树算法通过 “构建一棵压缩的前缀树(FP 树)”,仅需扫描两次数据就能完成频繁项集挖掘,是工业界处理大规模事务数据的首选方案。这篇文章会从 “为什么需要 FP 树” 讲起,用 “购物篮数据” 为案例,手把手拆解 FP 树的构建步骤和频繁模式挖掘过程,所有内容贴合入门认知,不堆砌复杂理论,只讲 “能看懂、能复现” 的实操逻辑。

一、先搞懂:为什么 FP 树比 Apriori 更高效?
要理解 FP 树的价值,首先得明白它要解决的 “Apriori 算法痛点”—— 这能帮你快速抓住 FP 树的核心优势。
1.1 Apriori 算法的 “低效陷阱”
Apriori 是早期的频繁项集挖掘算法,核心逻辑是 “生成候选项集→扫描数据验证”,但存在两个致命问题:
- 多次扫描数据:比如要挖掘 “3 项频繁集”,需要先扫描数据找 “1 项频繁集”,再扫描找 “2 项频繁集”,最后扫描找 “3 项频繁集”—— 数据量越大,扫描次数越多,耗时越长;
- 生成大量候选项集:比如 100 个 1 项频繁集,可能生成上万个 2 项候选项集,大部分候选项集最终会被验证为 “非频繁”,浪费计算资源。
举个例子:如果有 10 万条购物记录,Apriori 可能需要扫描 5-10 次数据,每次处理上万条候选项集,在普通电脑上可能要跑几小时;而 FP 树仅需扫描 2 次,几分钟就能出结果。
1.2 FP 树的核心改进:“一次建图,高效挖掘”
FP 树(Frequent Pattern Tree,频繁模式树)的改进思路很简单:
- 压缩数据:用 “前缀树” 把所有事务的频繁项按 “支持度降序” 存储,相同前缀的事务共享树枝,避免重复存储(比如 “f→c→a→m” 和 “f→c→a→b” 共享 “f→c→a” 前缀);
- 减少扫描:仅需扫描两次数据 —— 第一次统计频繁项,第二次构建 FP 树;
- 无候选项集:直接从 FP 树中 “生长” 出频繁项集,不用生成大量候选,大幅减少计算量。
简单说,FP 树就像 “把杂乱的事务数据整理成一棵有序的树”,后续挖掘频繁项集只需 “遍历树”,而不是 “反复扫数据”。
二、FP 树算法的核心基础:3 个关键概念要先吃透
在动手构建 FP 树前,必须先理解 3 个基础概念 —— 这些是后续步骤的 “语言基础”,入门一定要记牢。
2.1 频繁项集:FP 树的 “构建原料”
频繁项集是指 “支持度≥最小支持度阈值” 的物品集合(比如最小支持度 = 2,出现次数≥2 的物品或物品组合)。FP 树只处理频繁项,非频繁项会被直接过滤(因为非频繁项不可能构成频繁项集)。
举个例子:如果 “鸡蛋” 在 100 条购物记录中只出现 1 次(支持度 = 1% < 最小支持度 2%),则 “鸡蛋” 是非频繁项,所有包含 “鸡蛋” 的事务都会先删除 “鸡蛋” 再处理。
2.2 前缀树(Prefix Tree):FP 树的 “数据结构”
FP 树是一棵特殊的前缀树,特点是:
- 根节点为 null:不代表任何物品;
- 每个节点代表一个频繁项:节点包含 “物品名称” 和 “支持度计数”(该节点代表的物品在当前前缀路径上的出现次数);
- 相同前缀共享树枝:比如事务 “f→c→a→m” 和 “f→c→a→p”,前 3 个物品 “f→c→a” 完全相同,会共享这部分树枝,只在 “a” 节点后分别添加 “m” 和 “p” 节点;
- 按支持度降序排列:支持度越高的频繁项,离根节点越近(比如 “f” 支持度最高,直接连在根节点下;“c” 次之,连在 “f” 下)—— 这样能最大化前缀共享,压缩树的规模。
2.3 项头表(Header Table):FP 树的 “导航地图”
项头表是辅助挖掘频繁项集的 “索引”,包含 3 列:
- 频繁项:所有 1 项频繁项,按支持度降序排列;
- 支持度:该频繁项在所有事务中的总出现次数;
- 节点指针:指向 FP 树中所有包含该频繁项的节点(比如 “p” 的指针会指向树中所有 “p” 节点)—— 通过指针能快速找到某频繁项的所有出现位置,避免遍历整棵树。
三、手把手构建 FP 树:以购物篮数据为例(Step by Step)
这是 FP 树算法的核心环节。我们以一份真实的购物篮事务数据为案例,严格按照 “两次扫描数据” 的流程,一步步构建 FP 树。所有数据和步骤均基于真实的关联分析逻辑,确保你能跟着复现。
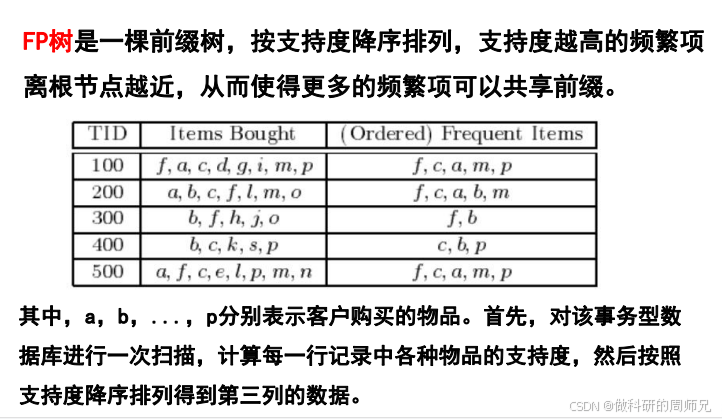
3.1 准备工作:事务数据与最小支持度
假设我们有 5 条购物事务数据(TID 为事务 ID,Items Bought 为用户购买的物品),设定最小支持度阈值 = 2(即出现次数≥2 的物品才是频繁项):
| TID | Items Bought(购买物品) |
|---|---|
| 100 | f, a, c, d, g, i, m, p |
| 200 | a, b, c, f, l, m, o |
| 300 | b, f, h, j, o |
| 400 | b, c, k, s, p |
| 500 | a, f, c, e, l, p, m, n |
3.2 第一次扫描数据:筛选 1 项频繁集,生成项头表
第一次扫描的目标是 “找出所有 1 项频繁项,过滤非频繁项”,具体步骤:
统计每个物品的支持度(出现次数):
- f:出现在 TID100、200、300、500 → 4 次;
- a:出现在 TID100、200、500 → 3 次;
- c:出现在 TID100、200、400、500 → 4 次;
- m:出现在 TID100、200、500 → 3 次;
- p:出现在 TID100、400、500 → 3 次;
- b:出现在 TID200、300、400 → 3 次;
- d, g, i, l, o, h, j, k, s, e, n:均只出现 1 次 → 非频繁项。
筛选 1 项频繁集:保留支持度≥2 的物品,得到频繁项列表:[f (4), c (4), a (3), m (3), p (3), b (3)](按支持度降序排列,支持度相同的顺序可微调,不影响结果)。
生成项头表:
| 频繁项 | 支持度 | 节点指针(待构建 FP 树后补充) |
|--------|--------|------------------------------|
| f | 4 | 指向树中所有 “f” 节点 |
| c | 4 | 指向树中所有 “c” 节点 |
| a | 3 | 指向树中所有 “a” 节点 |
| m | 3 | 指向树中所有 “m” 节点 |
| p | 3 | 指向树中所有 “p” 节点 |
| b | 3 | 指向树中所有 “b” 节点 |处理每条事务:删除事务中的非频繁项,剩余频繁项按 “项头表顺序(支持度降序)” 排序,得到 “有序频繁项列表”—— 这是第二次扫描构建 FP 树的输入:
| TID | 原始事务(去非频繁项) | 有序频繁项列表(按支持度降序) |
|------|------------------------|--------------------------------|
| 100 | f, a, c, m, p | f, c, a, m, p |
| 200 | a, b, c, f, m | f, c, a, b, m |
| 300 | b, f | f, b |
| 400 | b, c, p | c, b, p |
| 500 | a, f, c, p, m | f, c, a, m, p |
3.3 第二次扫描数据:构建 FP 树(5 步完成)
第二次扫描的目标是 “将有序频繁项列表逐行插入 FP 树”,每插入一条事务,就更新树的节点计数。我们一步步来:
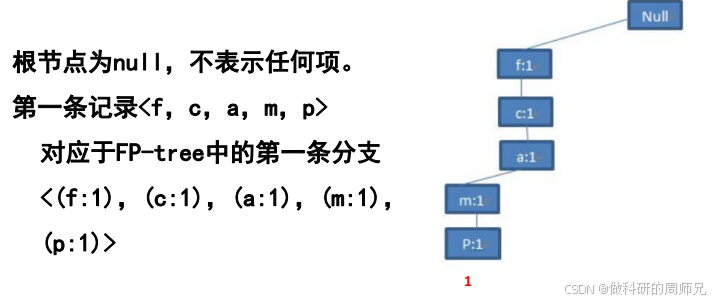
Step 1:插入第一条事务【f, c, a, m, p】
- 根节点(null)下无 “f” 节点,新建 “f:1” 节点(“f” 表示物品,“1” 表示支持度计数);
- “f:1” 下无 “c” 节点,新建 “c:1” 节点;
- “c:1” 下无 “a” 节点,新建 “a:1” 节点;
- “a:1” 下无 “m” 节点,新建 “m:1” 节点;
- “m:1” 下无 “p” 节点,新建 “p:1” 节点;
- 此时 FP 树结构:
null → f:1 → c:1 → a:1 → m:1 → p:1
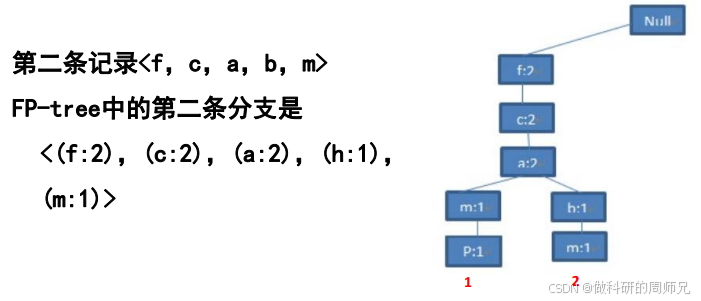
Step 2:插入第二条事务【f, c, a, b, m】
- 根节点下已有 “f:1”,计数更新为 “f:2”;
- “f:2” 下已有 “c:1”,计数更新为 “c:2”;
- “c:2” 下已有 “a:1”,计数更新为 “a:2”;
- “a:2” 下无 “b” 节点,新建 “b:1” 节点;
- “a:2” 下无 “m” 节点(注意:“m” 在第一条事务中在 “a” 下的 “p” 前,这里 “b” 和 “m” 是不同分支),新建 “m:1” 节点;
- 此时 FP 树结构:
null → f:2 → c:2 → a:2 → 「b:1」、「m:1」
↓
p:1(继承自第一条事务的 “m:1” 下)
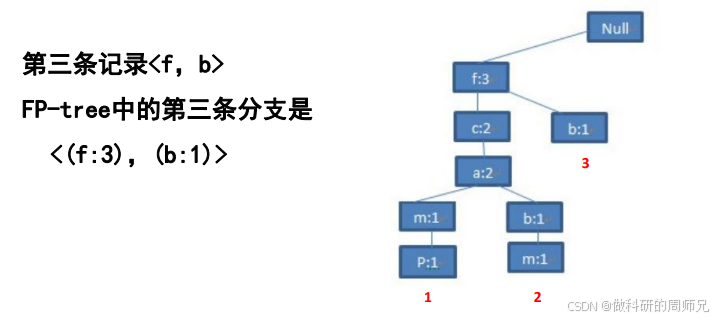
Step 3:插入第三条事务【f, b】
- 根节点下已有 “f:2”,计数更新为 “f:3”;
- “f:3” 下无 “b” 节点(之前 “b” 在 “a” 下,这里是新分支),新建 “b:1” 节点;
- 此时 FP 树结构:
null → f:3 → 「c:2 → a:2 → b:1、m:1 → p:1」、「b:1」
Step 4:插入第四条事务【c, b, p】
- 根节点下无 “c” 节点(“c” 之前在 “f” 下,这里是新分支),新建 “c:1” 节点;
- “c:1” 下无 “b” 节点,新建 “b:1” 节点;
- “b:1” 下无 “p” 节点,新建 “p:1” 节点;
- 此时 FP 树结构:
null → 「f:3 → c:2 → a:2 → b:1、m:1 → p:1;b:1」、「c:1 → b:1 → p:1」
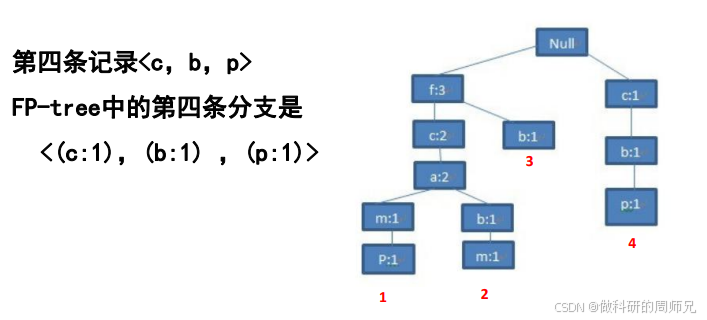
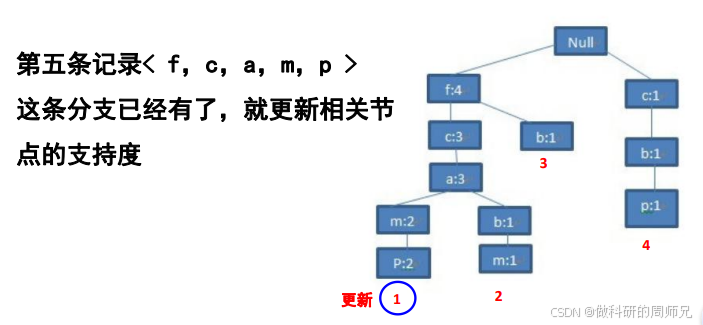
Step 5:插入第五条事务【f, c, a, m, p】
根节点下已有 “f:3”,计数更新为 “f:4”;
“f:4” 下已有 “c:2”,计数更新为 “c:3”;
“c:3” 下已有 “a:2”,计数更新为 “a:3”;
“a:3” 下已有 “m:1”,计数更新为 “m:2”;
“m:2” 下已有 “p:1”,计数更新为 “p:2”;
此时 FP 树结构(最终版):
null → 「f:4 → c:3 → a:3 → b:1、m:2 → p:2;b:1」、「c:1 → b:1 → p:1」补充项头表的节点指针:比如 “p” 的指针指向 “m:2” 下的 “p:2” 和 “b:1” 下的 “p:1”;“b” 的指针指向 “a:3” 下的 “b:1”、“f:4” 下的 “b:1”、“c:1” 下的 “b:1”。
四、从 FP 树挖掘频繁项集:“逆序遍历,生长模式”
构建完 FP 树后,下一步就是 “挖掘频繁项集”。核心逻辑是 “从项头表的最后一项(支持度最低的频繁项)开始,找它的所有前缀链,构建条件 FP 树,再递归挖掘”—— 这样能保证不遗漏任何频繁项集。
我们以 “挖掘包含 p 的频繁项集” 为例(p 是项头表最后一项),演示完整挖掘过程:
4.1 第一步:找 “p” 的所有节点链(通过项头表指针)
项头表中 “p” 的指针指向两个节点:
- 节点 1:位于路径「f→c→a→m→p」,p 的计数 = 2(表示这条路径在事务中出现 2 次,对应 TID100 和 TID500);
- 节点 2:位于路径「c→b→p」,p 的计数 = 1(表示这条路径出现 1 次,对应 TID400)。
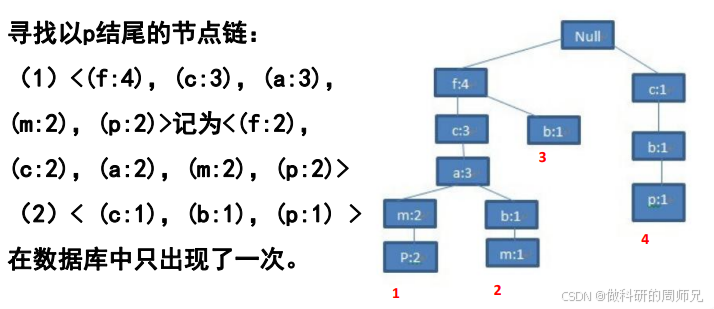
4.2 第二步:提取 “p” 的前缀链(去掉 p 节点,保留前缀和计数)
前缀链是 “p 节点所在路径中,p 之前的所有节点”,且计数与 p 节点的计数一致(因为前缀和 p 同时出现):
- 节点 1 的前缀链:「f:2, c:2, a:2, m:2」(p 计数 = 2,所以前缀节点计数均为 2);
- 节点 2 的前缀链:「c:1, b:1」(p 计数 = 1,所以前缀节点计数均为 1)。
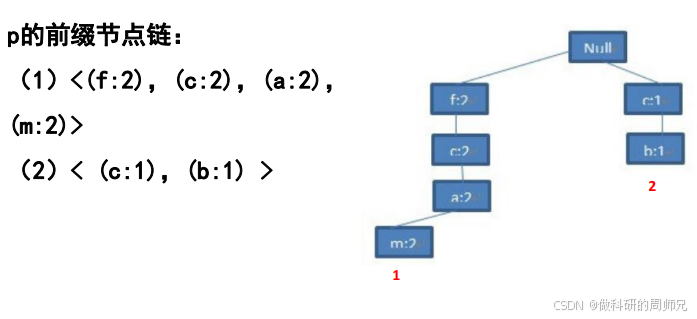
4.3 第三步:构建 “p 的条件 FP 树”
条件 FP 树是 “仅包含前缀链中频繁项” 的子树,构建步骤:
- 统计前缀链中各物品的支持度:
- f:2 次,c:2+1=3 次,a:2 次,m:2 次,b:1 次;
- 筛选条件频繁项(支持度≥最小支持度 2):f (2)、c (3)、a (2)、m (2)(b 支持度 = 1,过滤);
- 按支持度降序排序前缀链:
- 前缀链 1「f:2, c:2, a:2, m:2」→ 顺序不变(已符合降序);
- 前缀链 2「c:1, b:1」→ 去掉 b,只剩「c:1」(但 c 支持度 = 3≥2,保留);
- 构建条件 FP 树:
- 插入「f:2, c:2, a:2, m:2」→ 形成路径「f:2→c:2→a:2→m:2」;
- 插入「c:1」→ 形成路径「c:1」(与现有 “c:2” 共享根节点,c 总计数更新为 3);
- 最终 p 的条件 FP 树:null → 「f:2→c:3→a:2→m:2」。
4.4 第四步:从条件 FP 树中生成 “包含 p 的频繁项集”
递归挖掘条件 FP 树中的频繁项集,再与 “p” 组合,得到所有包含 p 的频繁项集:
- 条件 FP 树中的频繁项集(不包含 p):{f}, {c}, {a}, {m}, {f,c}, {f,a}, {f,m}, {c,a}, {c,m}, {a,m}, {f,c,a}, {f,c,m}, {f,a,m}, {c,a,m}, {f,c,a,m};
- 与 “p” 组合,得到包含 p 的频繁项集:{f,p}, {c,p}, {a,p}, {m,p}, {f,c,p}, {f,a,p}, {f,m,p}, {c,a,p}, {c,m,p}, {a,m,p}, {f,c,a,p}, {f,c,m,p}, {f,a,m,p}, {c,a,m,p}, {f,c,a,m,p};
- 验证支持度:比如 {f,c,a,m,p} 的支持度 = 2(对应 TID100 和 TID500),≥最小支持度 2,是频繁项集;{c,b,p} 的支持度 = 1 < 2,是非频繁项集,过滤。
4.5 第五步:重复挖掘其他频繁项
按项头表逆序(b→m→a→c→f),重复上述 4 步,挖掘包含每个频繁项的频繁项集,最终合并所有结果,得到完整的频繁项集列表。
五、FP 树算法的优势与典型应用场景
FP 树能成为关联分析的主流算法,核心在于它的高效性和实用性,我们总结它的优势和应用场景,帮你理解 “学了能用来做什么”。
5.1 FP 树的三大核心优势
- 高效性:仅扫描两次数据,避免 Apriori 的多次扫描;无候选项集,直接从树中挖掘,计算成本低;
- 可扩展性:支持百万级、千万级事务数据,树结构压缩率高(比如 100 万条事务可能压缩成几万节点的树);
- 灵活性:支持任意最小支持度阈值,阈值调整后只需重新构建项头表和 FP 树,无需重新扫描原始数据(若原始事务已预处理为有序频繁项列表)。
5.2 FP 树的典型应用场景
- 电商购物篮分析:挖掘 “买了 A 又买 B” 的频繁项集,用于商品推荐(如 “购物车推荐”)、货架摆放(如把频繁一起购买的商品放在相邻货架);
- 零售行业促销:比如挖掘到 “薯片 + 可乐” 是频繁项集,可推出 “买薯片送可乐” 的促销活动,提升销量;
- 日志分析:分析用户访问日志,挖掘 “访问页面 A 后又访问页面 B” 的频繁路径,优化网站结构(如把页面 B 设为页面 A 的跳转链接);
- 医疗数据分析:挖掘 “症状 A + 症状 B→疾病 C” 的频繁模式,辅助医生诊断(比如 “咳嗽 + 发烧→感冒” 的频繁项集)。
六、入门学生学习 FP 树的建议
对于刚接触 FP 树的学生,不需要一开始就实现复杂的代码,重点是理解 “构建流程” 和 “挖掘逻辑”,可以按以下步骤学习:
- 手动复现案例:用本文的购物篮数据,手动画一遍 FP 树的构建过程(从 Step1 到 Step5),再手动挖掘包含 p 的频繁项集 —— 这是理解 FP 树最有效的方式;
- 用工具简化实现:推荐用 Python 的
pyfpgrowth库或mlxtend库,输入简单事务数据,调用 API 生成 FP 树和频繁项集,观察结果与手动计算是否一致; - 理解核心逻辑,而非代码细节:入门阶段不用深究 “如何用 Python 实现树的节点插入和指针维护”,重点记住 “两次扫描数据→构建 FP 树→逆序挖掘条件 FP 树” 的核心流程;
- 结合实际场景思考:比如思考 “如何用 FP 树分析学校食堂的消费数据,挖掘学生常点的菜品组合”,把理论和实际结合起来。
六、总结:FP 树算法的 “核心逻辑链”
最后用一条清晰的逻辑链,帮你串联 FP 树的完整流程:
- 问题:Apriori 算法多次扫描数据、生成大量候选项集,效率低;
- 方案:用 FP 树压缩数据,仅扫描两次数据,无候选项集挖掘;
- 步骤:
① 第一次扫描:统计 1 项频繁集,生成项头表,处理事务为有序频繁项列表;
② 第二次扫描:插入有序频繁项,构建 FP 树,补充项头表指针;
③ 挖掘频繁项集:逆序遍历项头表,构建条件 FP 树,递归生成频繁项集; - 应用:购物篮分析、日志分析、医疗诊断等需要挖掘频繁模式的场景。
FP 树是关联分析的 “核心工具”,理解它的逻辑后,再学习更复杂的关联算法(如 FP-Growth 的优化版)会更轻松。如果这篇文章里有哪个步骤没搞懂,欢迎在评论区留言,我们一起拆解!
