Python实现点云AABB和OBB包围盒
今天我们来介绍一个点云中经常用到的操作,包围盒计算。众索粥汁,点云数据是由一系列离散的三维点表示的物体或场景。为了简化对点云数据的处理,经常使用包围盒(Bounding Box)来近似表示点云的形状。包围盒是一种简单的几何结构,它可以快速地提供点云的大致范围,用于碰撞检测、空间划分等多种应用。
## 一、点云包围盒概述
点云数据是由一系列离散的三维点表示的物体或场景。为了简化对点云数据的处理,经常使用包围盒(Bounding Box)来近似表示点云的形状。包围盒是一种简单的几何结构,它可以快速地提供点云的大致范围,用于碰撞检测、空间划分等多种应用。
### (一)AABB(Axis - Aligned Bounding Box,轴对齐包围盒)
- **定义**
- AABB是一种与坐标轴对齐的矩形框。在三维空间中,它有六个面,每个面都平行于坐标轴。也就是说,AABB的边总是沿着x、y、z轴方向。
- **计算过程**
- 对于给定的点云数据,首先需要找到点云在每个坐标轴方向上的最大值和最小值。
- 例如,对于点云中的点 \( P(x, y, z) \),遍历所有点,记录下 \( x_{min} \)、\( x_{max} \)、\( y_{min} \)、\( y_{max} \)、\( z_{min} \) 和 \( z_{max} \)。
- AABB的八个顶点可以通过这六个极值来确定。具体来说,AABB的最小顶点坐标为 \( (x_{min}, y_{min}, z_{min}) \),最大顶点坐标为 \( (x_{max}, y_{max}, z_{max}) \),其他顶点坐标可以通过组合这些极值来得到。
- 计算AABB的过程相对简单,因为它不需要考虑点云的旋转等复杂情况,只需要在每个轴方向上进行线性扫描即可。### (二)OBB(Oriented Bounding Box,方向包围盒)
- **定义**
- OBB是一种可以任意旋转的矩形框。它不像AABB那样受限于坐标轴,而是可以根据点云的形状和方向来调整自己的方向,从而更紧凑地包围点云。
- **计算过程**
- **主成分分析(PCA)方法**
- 首先,计算点云的均值,将点云数据平移到原点附近,这有助于后续的计算。
- 然后,构建点云的协方差矩阵。对于点云中的每个点 \( P(x, y, z) \),协方差矩阵 \( C \) 的计算公式为:
\[ C = \frac{1}{n} \sum_{i = 1}^{n} (P_i - \mu)(P_i - \mu)^T \]
其中,\( n \) 是点云中点的数量,\( \mu \) 是点云的均值向量,\( P_i \) 是点云中的第 \( i \) 个点。
- 接下来,对协方差矩阵进行特征分解,得到三个主成分方向。这三个方向是点云数据在空间中变化最大的方向,可以作为OBB的轴方向。
- 最后,根据这三个轴方向,计算点云在每个轴方向上的投影范围,确定OBB的大小。具体来说,对于每个轴方向,计算点云在该方向上的投影长度,得到OBB的边长。
- **其他方法**
- 除了PCA方法,还可以使用旋转卡壳(Rotating Calipers)方法等来计算OBB。旋转卡壳方法主要是通过寻找点云的凸包,然后在凸包上寻找能够最小化包围盒面积或体积的旋转方向。不过这种方法相对复杂,计算量也比较大。## 二、应用
### (一)碰撞检测
- **AABB的应用**
- 在碰撞检测中,AABB可以快速地进行初步判断。如果两个AABB没有重叠,那么它们所代表的物体或点云肯定不会发生碰撞。这是因为AABB的边界是轴对齐的,判断两个AABB是否重叠只需要比较它们在每个坐标轴方向上的范围即可。例如,对于两个AABB,分别用 \( [x_{min1}, x_{max1}] \)、\( [y_{min1}, y_{max1}] \)、\( [z_{min1}, z_{max1}] \) 和 \( [x_{min2}, x_{max2}] \)、\( [y_{min2}, y_{max2}] \)、\( [z_{min2}, z_{max2}] \) 表示它们在x、y、z轴方向上的范围,如果 \( x_{max1} < x_{min2} \) 或 \( x_{min1} > x_{max2} \) 或 \( y_{max1} < y_{min2} \) 或 \( y_{min1} > y_{max2} \) 或 \( z_{max1} < z_{min2} \) 或 \( z_{min1} > z_{max2} \),那么这两个AABB不重叠。
- 由于AABB的计算和比较都非常简单,它在实时碰撞检测系统中(如游戏引擎中的物体碰撞检测)被广泛使用,用于快速剔除不可能发生碰撞的物体对,从而减少后续精确碰撞检测的计算量。
- **OBB的应用**
- OBB在碰撞检测中可以提供更精确的碰撞判断。因为OBB可以根据物体的形状和方向进行调整,所以它能够更紧密地包围物体。在一些对碰撞精度要求较高的场景中(如机器人路径规划中,需要精确判断机器人与周围障碍物的碰撞情况),使用OBB可以避免AABB可能出现的过度包围导致的误判。
- 但是,OBB之间的碰撞检测比AABB复杂。通常需要使用分离轴定理(Separating Axis Theorem)等方法来判断两个OBB是否重叠。分离轴定理的基本思想是:如果能够找到一个轴,使得两个OBB在该轴上的投影不重叠,那么这两个OBB就不重叠。对于三维空间中的OBB,需要考虑多个可能的分离轴,包括OBB的边的方向以及两个OBB边的叉积方向等。### (二)空间划分
- **AABB的应用**
- 在空间划分算法(如八叉树空间划分)中,AABB可以作为划分的基本单元。通过将点云数据包围在一个AABB内,然后根据一定的规则(如将AABB沿坐标轴方向等分)将AABB划分为更小的子AABB,可以逐步细化空间划分。这种基于AABB的空间划分方法简单高效,适用于大规模点云数据的组织和管理,例如在三维地理信息系统(GIS)中,用于存储和查询地理空间数据。
- **OBB的应用**
- OBB也可以用于空间划分,但它的划分方式更加灵活。由于OBB可以根据点云的方向进行调整,所以它可以更好地适应点云的形状。在一些复杂的场景建模中(如对建筑物内部空间进行建模,建筑物内部的房间、走廊等形状各异),使用OBB进行空间划分可以更准确地表示空间结构,减少空间划分的冗余。
一、包围盒计算程序
import open3d as o3ddef load_point_cloud(file_path):"""加载点云文件"""pcd = o3d.io.read_point_cloud(file_path)return pcddef compute_and_display_aabb(pcd):"""计算并显示 AABB 包围盒"""aabb = pcd.get_axis_aligned_bounding_box()aabb.color = (1, 0, 0) # 设置 AABB 的颜色为红色print("AABB 顶点坐标:")for i, vertex in enumerate(aabb.get_box_points()):print(f"顶点 {i}: {vertex}")o3d.visualization.draw_geometries([pcd, aabb], window_name="AABB")def compute_and_display_obb(pcd):"""计算并显示 OBB 包围盒"""obb = pcd.get_oriented_bounding_box()obb.color = (0, 1, 0) # 设置 OBB 的颜色为绿色print("OBB 顶点坐标:")for i, vertex in enumerate(obb.get_box_points()):print(f"顶点 {i}: {vertex}")o3d.visualization.draw_geometries([pcd, obb], window_name="OBB")def main():file_path = 'E:/CSDN/规则点云/bunny.pcd'pcd = load_point_cloud(file_path)while True:print("\n请选择操作:")print("1. 计算并显示 AABB 包围盒")print("2. 计算并显示 OBB 包围盒")print("3. 退出")choice = input("请输入选项(1, 2 或 3):")if choice == '1':compute_and_display_aabb(pcd)elif choice == '2':compute_and_display_obb(pcd)elif choice == '3':print("退出程序。")breakelse:print("无效的选项,请重新输入。")if __name__ == "__main__":main()二、包围盒计算结果
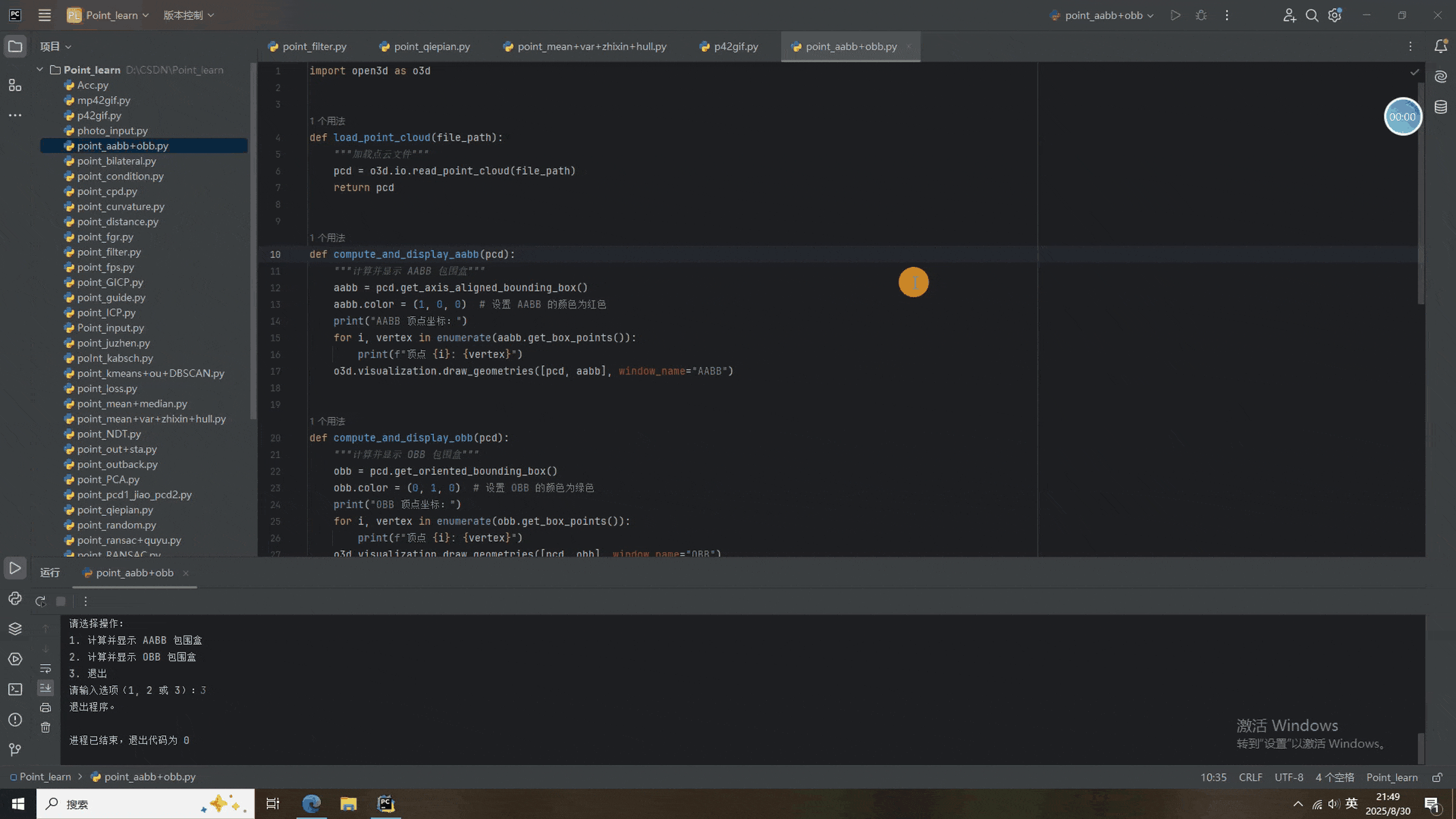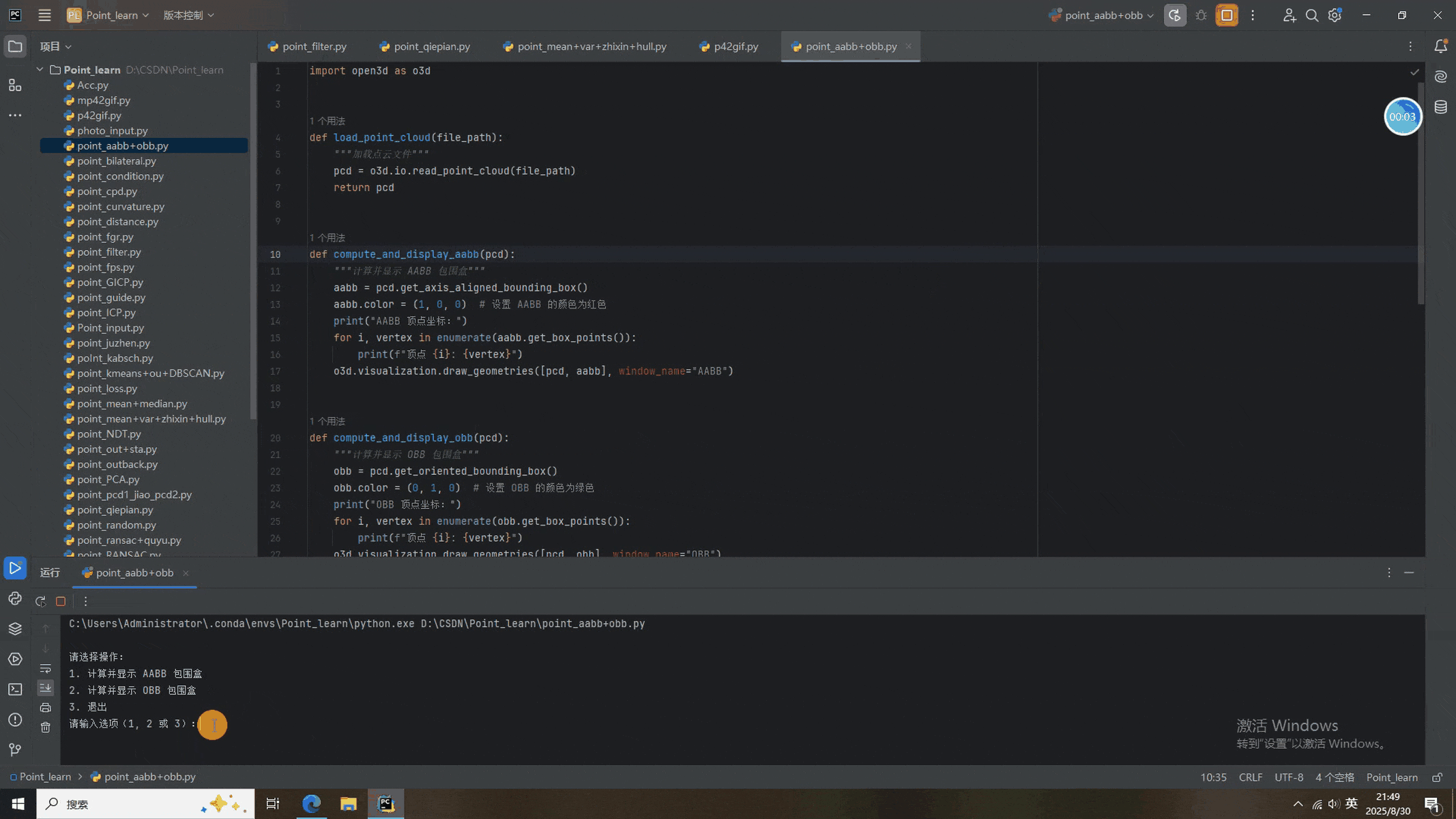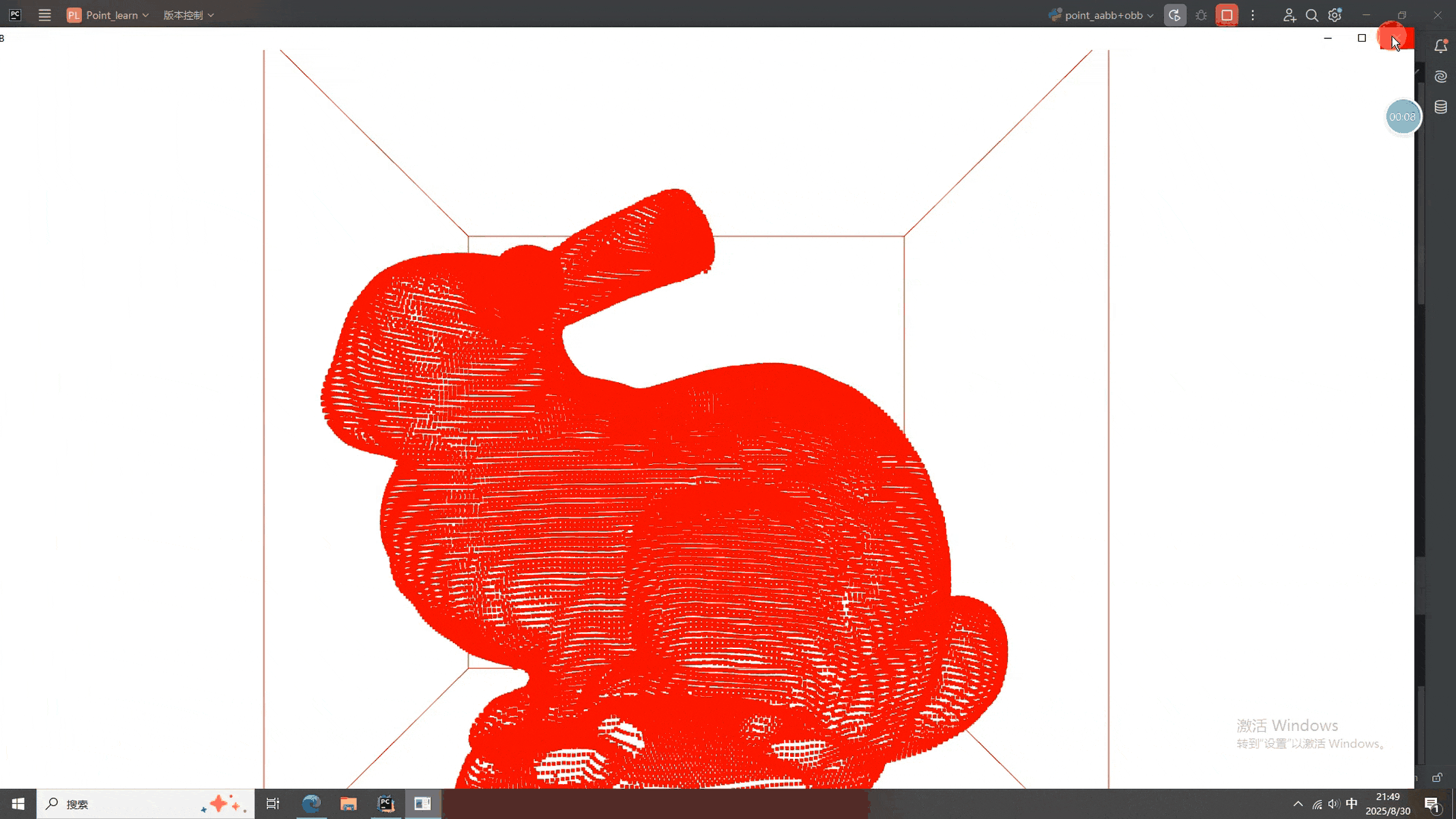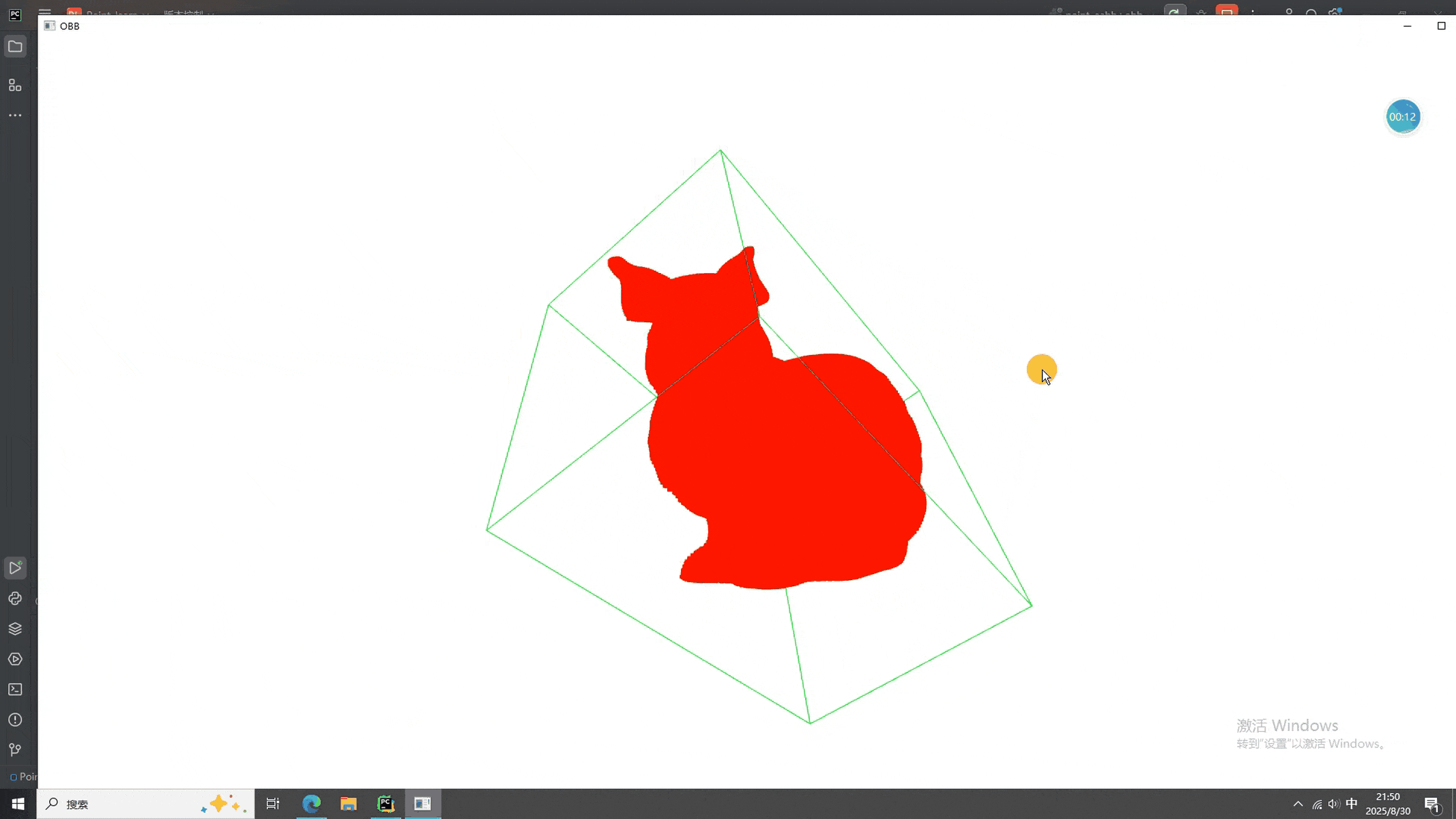
大家可以看到,包围盒被很顺利的计算了出来,快快夸夸我(傲娇)。就酱,下次见^-^
