接雨水,leetCode热题100,C++实现
题目来源:leetCode
42. 接雨水 - 力扣(LeetCode)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

双指针法
class Solution {
public:int trap(vector<int>& height) {int left = 0, right = height.size() - 1;int leftMax = 0, rightMax = 0;int water = 0;while (left < right) {// 更新左右最大值leftMax = max(leftMax, height[left]);rightMax = max(rightMax, height[right]);if (height[left] < height[right]) {water += leftMax - height[left];left++;} else {water += rightMax - height[right];right--;}}return water;}
};这道题不能只看代码,我们这样理解,我们遍历数组,比如使用for循环时,i是当前位置
然后我们需要计算的是当前位置的水量,最后把所有位置加起来即可
那么当前位置的水量怎么算?我们之前也做过一道类似的题,假设数组是[1,0,2],当前位置为1,可以接水量为1,水量 = 左右两边最低的柱子*宽度,这里就是1*1
那假设数组为[2,1,3],那么当前位置还是1(因为最左边和最右边的位置肯定不能接到水),此时水量还需要减去当前位置柱子的高度才行,是2*1-1=1
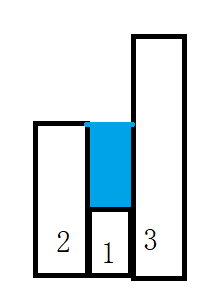
水量如图所示,因为柱子也占了空间,所以要减去当前位置的柱子高度
那我们往大扩展,来看数组[1,2,0,1,0,3]
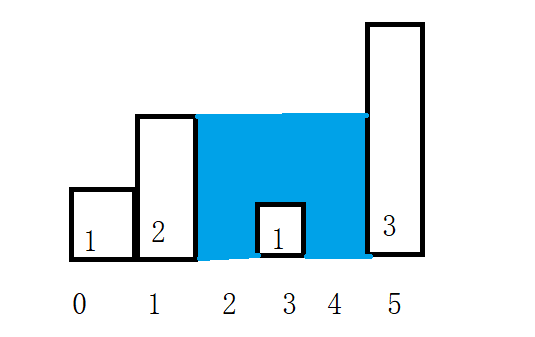
如图所示,位置1和位置5是边界,所以水量为0
我们看位置1,左边的柱子高度为1,右边的柱子有高度为3的,也有高度为1的,所以水量是高度最低的柱子,也就是左边位置1的柱子,然后减去当前位置柱子高度,为1-2=-1,但是没有负数,所以这里为0
接着看位置2,我们在位置1的时候就发现,右边柱子有高度为3的和高度为1的,为什么最后选择了高度为3的?我们看图就可以看出来,一目了然,因为高度为1的柱子挡不住,然后这里右边选择高度为3的柱子,所以当前位置的水量是min(2,3)*1-0=2,既左右两把高度最低的柱子,减去当前位置高度,注意,我们计算的一直是当前位置的水量,所以这里我们只计算位置2的水量
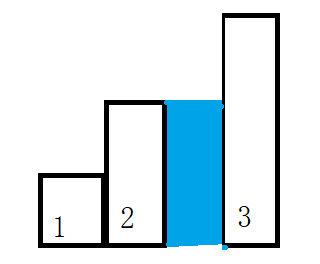
我们可以等效为将两边高度最高的柱子,直接移动到了当前位置的左右两侧,这样是不是就很醒目?
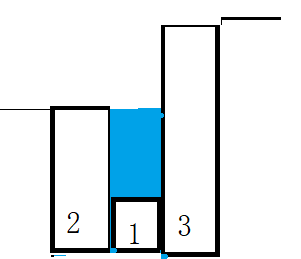
同样的理解,我们可以得到位置3的水量,后面以此类推
当然我们理解是这样理解,代码不是这样写的,此时我们已经搞懂了本题的逻辑,接下来轻松完成代码即可

核心是while循环,相当于我们用for循环遍历数组,接着选取左右两边最高的柱子,对于每一个位置,都要选取左右两边最高的柱子,假设数组有10个元素,当前位置是5,那么左边的柱子,我们需要从位置0到位置4所有出现的柱子中找到最高的柱子,右边也是同理,至于原因,我们在上面的图片里已经明白了,因为低的柱子挡不住水
然后比较左右两边柱子高低,计算当前位置水量,接着移动高度低的指针即可
动态规划法
class Solution {
public:int trap(vector<int>& height) {int n = height.size();if (n == 0)return 0;// 1. 计算每个位置左边的最大值vector<int> leftMax(n);leftMax[0] = height[0];for (int i = 1; i < n; i++) {leftMax[i] = max(leftMax[i - 1], height[i]);}// 2. 计算每个位置右边的最大值vector<int> rightMax(n);rightMax[n - 1] = height[n - 1];for (int i = n - 2; i >= 0; i--) {rightMax[i] = max(rightMax[i + 1], height[i]);}// 3. 计算总水量int water = 0;for (int i = 0; i < n; i++) {water += min(leftMax[i], rightMax[i]) - height[i];}return water;}
};说是动态规划法,其实思路还是和双指针法一样,只不过这次我们先进行预处理,计算出每一个位置的左边和右边的最大值,然后逐个计算每个位置的水量,最后相加,对于每个位置,水量 = min(左边最大值, 右边最大值) - 当前高度
