数据库攻略:“CMU 15-445”Project0:C++ Primer(2024 Fall)
一、前言
这个项目是作者认为一个非常好的项目,学习这个项目的过程你会学习到许多数据库之外的东西,例如它本身就是一个C++项目,你可以通过它学习Linux下的C++项目构建以及如何去测试C++项目, bustub 作为一个 C++ 编写的中小型项目涵盖了程序构建、代码规范、单元测试等众多要求,可以作为一个优秀的开源项目学习。。但由于网上的教程大多没有讲解过项目的配置过程,而官方的作业描述又不是足够清晰,所以作者准备将完成这个项目详细的过程记录下来。
二、环境部署
首先我们要去github上下载BusTub这个项目,我们的所有项目都是在这个数据库管理系统上编写的,当下载完成后就会看到下面这些文件:
首先我们来讲解每个文件夹的作用:
- build:用于构建项目的文件夹,防止污染源代码目录。
- build_support:构建支持工具,辅助项目编译、代码风格检查等。
- logo:项目的图标。
- src:这是项目的核心代码目录,包含数据库系统的主要实现,我们要编写的代码都将在这个目录中完成。
- test:包含单元测试和集成测试代码,验证各个模块的正确性,这是用于测试我们代码的目录。
- third_party:项目的第三方依赖库。
- tools:项目的工具函数。
了解完这些文件夹的作用我们就可以开始构建项目了。首先我们需要安装一些工具,如果你是符合版本的debian或者ubuntu,可以直接执行build_support/packages.sh来进行安装,但如果不是,比如作者使用的是kali,那么你就需要手动安装:
sudo apt update
sudo apt install cmake
sudo apt install clang-14 libc++-14-dev libc++abi-14-dev//编译器、标准库、运行时库
sudo apt install clang-format-14 clang-tidy-14//代码格式化工具、代码静态分析工具
sudo apt install libelf-dev libdwarf-dev libdw-dev binutils-dev//代码调试相关工具,libelf 是基础:提供 ELF 文件(Linux和BSD等系统的标准可执行文件格式,包含程序头、节表、符号表等结构)解析能力,是其他库的依赖。libdwarf(提供 DWARF(Debugging With Attributed Record Formats)调试信息的解析库。DWARF 是一种标准的调试信息格式,存储变量名、函数名、行号等调试所需信息) 和 libdw(基于 libdwarf 的高层封装库,提供更简洁的 API 访问 DWARF 信息。它还包含对 ELF 文件的扩展支持,可直接关联调试信息与二进制代码) 专注调试信息:基于 libelf 读取 DWARF 格式的调试数据。binutils-dev 提供高层工具链 API:可与上述库结合,构建完整的二进制分析工具。
mkdir build
cd build
CC=clang-14 CXX=clang++-14 //临时设置环境变量使用clang编译器,通常默认环境变量是使用gcc
cmake -DCMAKE_BUILD_TYPE=Debug .. //cmake编译需要使用命令指定CMakeList.txt文件的路径
make -j`nproc`
这里需要扩展一些知识:ABI 是应用程序二进制接口,它定义了二进制层面的规范,确保不同编译单元(如目标文件、库、可执行文件)能够正确交互。与 API(源代码层面的接口)不同,ABI 关注的是程序运行时的交互细节。而C++ 运行时库是一组底层函数和机制,支持 C++ 程序的运行。它补充了标准库(如)的功能,处理编译器无法直接生成的底层操作(异常处理、RTTI ),依赖于特定的 ABI 实现。
经过作者测试,该项目即使没有这些库也能编译成功,因为通常系统中自带gcc。
这里你可能遇到一些问题,例如:
Warning: An error occurred during the signature verification. The repository is not updated and the previous index files will be used. GPG error: https://mirrors.tuna.tsinghua.edu.cn/kali kali-rolling InRelease: The following signatures couldn't be verified because the public key is not available: NO_PUBKEY ED65462EC8D5E4C5
Notice: Repository 'https://mirrors.tuna.tsinghua.edu.cn/debian bookworm InRelease' changed its 'Version' value from '12.7' to '12.11'
Warning: Failed to fetch https://mirrors.tuna.tsinghua.edu.cn/kali/dists/kali-rolling/InRelease The following signatures couldn't be verified because the public key is not available: NO_PUBKEY ED65462EC8D5E4C5
Warning: Some index files failed to download. They have been ignored, or old ones used instead.
这个错误是由于系统缺少 Kali Linux 软件源的 GPG 公钥,导致无法验证仓库签名。错误提示 NO_PUBKEY ED65462EC8D5E4C5 表明系统中没有对应的公钥来验证清华源的 Kali 仓库签名,因此 apt 拒绝更新该仓库。
执行以下命令导入缺失的公钥(ED65462EC8D5E4C5 是错误中提示的公钥 ID):
# 导入公钥(替换为公钥后8位,即 D5E4C5)
sudo apt-key adv --keyserver keyserver.ubuntu.com --recv-keys ED65462EC8D5E4C5
-
说明:
keyserver.ubuntu.com是公开的 GPG 密钥服务器,通过公钥 ID 可获取对应公钥。 -
若命令失败:尝试更换密钥服务器(如
hkp://keyserver.pgp.net或hkp://pgp.mit.edu):sudo apt-key adv --keyserver hkp://keyserver.pgp.net --recv-keys ED65462EC8D5E4C5 -
GPG 签名:Linux 软件源通过 GPG 签名确保仓库内容未被篡改,系统需对应的公钥才能验证签名。
-
公钥缺失:当添加第三方源(如清华源的 Kali 仓库)时,系统可能没有预安装该源的公钥,导致验证失败。
-
手动导入:通过
apt-key工具从密钥服务器获取并安装公钥,即可解决签名验证问题。
然后可能碰到下面的问题:
Warning: https://mirrors.tuna.tsinghua.edu.cn/kali/dists/kali-rolling/InRelease: Key is stored in legacy trusted.gpg keyring (/etc/apt/trusted.gpg), see the DEPRECATION section in apt-key(8) for details.
这个警告是由于 apt 工具在新版本中对 GPG 密钥的存储方式进行了调整,旧的 trusted.gpg 密钥环已被标记为过时(deprecated),而你的系统中仍在使用这种传统方式存储 Kali 源的密钥。
- 早期的 apt 工具将所有 GPG 公钥存储在
/etc/apt/trusted.gpg或/etc/apt/trusted.gpg.d/目录下。 - 从 Debian 11(Bullseye)、Ubuntu 20.04 开始,官方推荐将密钥存储在
/etc/apt/keyrings/目录下,并通过源配置文件显式指定密钥路径,以提高安全性(避免全局信任所有密钥)。 - 你的系统检测到 Kali 源的密钥仍存放在旧的
trusted.gpg中,因此提示警告(但不影响功能)。 - 新的密钥管理方式:通过
signed-by在源配置中显式指定密钥文件,避免了全局信任所有密钥的安全风险。 - 兼容性:旧的
trusted.gpg仍能工作,但 apt 会提示警告,未来可能完全废弃。
按以下步骤将密钥迁移到新的存储位置:
1. 创建新的密钥存储目录
sudo mkdir -p /etc/apt/keyrings
2. 导出旧密钥并存储到新位置
先查看旧密钥环中的 Kali 源密钥(ED65462EC8D5E4C5 是之前的密钥 ID):
sudo apt-key list | grep -A 1 "ED65462EC8D5E4C5"
然后导出该密钥到新目录:
sudo apt-key export ED65462EC8D5E4C5 | sudo gpg --dearmour -o /etc/apt/keyrings/kali-archive-keyring.gpg
--dearmour:将 ASCII 格式的密钥转换为二进制.gpg格式(新方式要求)。
3. 修改 Kali 源的配置文件
编辑清华源的 Kali 配置(通常在 /etc/apt/sources.list 或 /etc/apt/sources.list.d/ 下的文件):
sudo nano /etc/apt/sources.list
找到 Kali 源的行,添加 signed-by 参数指定新的密钥路径:
# 原配置
# deb https://mirrors.tuna.tsinghua.edu.cn/kali kali-rolling main non-free contrib# 修改后(添加 signed-by)
deb [signed-by=/etc/apt/keyrings/kali-archive-keyring.gpg] https://mirrors.tuna.tsinghua.edu.cn/kali kali-rolling main non-free contrib
这里需要注意,如果启用了deb-src源则这个源也要修改,否则会报冲突,因为没有显式指定密钥路径的还是:
Error: Conflicting values set for option Signed-By regarding source https://mirrors.tuna.tsinghua.edu.cn/kali/ kali-rolling: /etc/apt/keyrings/kali-archive-keyring.gpg !=
Error: The list of sources could not be read.
4. 删除旧密钥(可选,彻底清理)
sudo apt-key del ED65462EC8D5E4C5
5. 更新源验证效果
sudo apt update
此时警告应消失,源可正常更新。
至此我们的环境部署环境也就到此结束了,后面将开始完成我们的项目了。
第0个项目:C++ Primer 任务1
我们先来介绍一下这个项目的背景,即为什么要做:
想象一下,要统计一个网站一天内的独立访问用户数量:对于小型网站(只有少数用户),这很简单 —— 只需用列表存储所有用户,再检查重复即可。但对于大型网站(数十亿用户),这种方法就完全不可行了:存储所有用户会导致内存耗尽,检查重复的过程也会异常缓慢,效率极低。
HyperLogLog(简称 HLL)是一种概率性数据结构,专门用于跟踪大型数据集的 “基数”(即唯一元素的数量)。它非常适合上述场景:当需要统计海量数据流中的独立元素数量,却不需要存储每个元素时,HLL 是理想选择。
HLL 的核心优势在于:通过巧妙的哈希机制和紧凑的数据结构,用远少于传统方法的内存,就能对唯一元素数量做出较准确的估计。这让它成为现代数据库分析中的关键工具。
HLL 的概率计数机制基于以下几个关键参数:
- b:哈希值二进制表示中,用于确定 “寄存器索引” 的初始位数(即前 b 位)。
- m:寄存器(也称为 “桶”,两者可互换使用)的数量,等于 2^b(即 m=2^b)。可以理解为 HLL 内部的 “存储单元” 总数。
- p:哈希值二进制表示中,“最左侧 1 的位置”(即最高有效位的 1 所在的位置),计算方式为 “从左侧开始的前导零数量 + 1”。
计算公式如下:
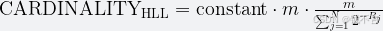
我们需要实现的函数都被声明在了src/include/primer/hyperloglog.h文件中:
- HyperLogLog(inital_bits):构造函数(提供前导位参数b)。
- GetCardinality():返回给定集的基数值
- AddElem(val):计算值并将其放入寄存器中。
- ComputeCardinality():根据上述公式计算基数。
上面四个函数是核心函数,除此之外,您还可以实现辅助函数来实现上述内容(可以根据需要添加更多):
- ComputeBinary(hash_t hash):它计算给定哈希值的二进制文件。哈希值应转换为 64 位二进制流(否则测试可能会失败)。
- PositionOfLeftmostOne(…):计算最左边的 1 的位置。
要计算哈希值,您可以使用给定的函数:
- CalculateHash(…): 计算哈希
我们要做的就是在src/primer/hyperloglog.cpp文件中实现它们:
#include "primer/hyperloglog.h"namespace bustub {/** @brief 参数化构造函数。 */
template <typename KeyType>
HyperLogLog<KeyType>::HyperLogLog(int16_t n_bits) : cardinality_(0) {}/*** @brief 计算二进制值的函数。** @param[in] hash* @returns 给定哈希值的二进制表示*/
template <typename KeyType>
auto HyperLogLog<KeyType>::ComputeBinary(const hash_t &hash) const -> std::bitset<BITSET_CAPACITY> {/** @TODO(学生) 实现此函数! */return {0};
}/*** @brief 计算前导零的函数。** @param[in] bset - 给定位集的二进制值* @returns 给定位集的前导零数量*/
template <typename KeyType>
auto HyperLogLog<KeyType>::PositionOfLeftmostOne(const std::bitset<BITSET_CAPACITY> &bset) const -> uint64_t {/** @TODO(学生) 实现此函数! */return 0;
}/*** @brief 向HyperLogLog中添加一个值。** @param[in] val - 添加到HyperLogLog中的值*/
template <typename KeyType>
auto HyperLogLog<KeyType>::AddElem(KeyType val) -> void {/** @TODO(学生) 实现此函数! */
}/*** @brief 计算基数的函数。*/
template <typename KeyType>
auto HyperLogLog<KeyType>::ComputeCardinality() -> void {/** @TODO(学生) 实现此函数! */
}template class HyperLogLog<int64_t>;
template class HyperLogLog<std::string>;} // namespace bustub
现在我们已经知道应该做些什么了,下面就要开始解决怎么做的问题,首先我们要详细的了解HLL的机制与原理。
HLL的机制
1. 哈希与二进制转换
HyperLogLog 的核心思想是利用哈希函数将任意类型的数据(如字符串、用户 ID)映射为均匀分布的二进制值。以字符串 “A great database is a great life” 为例:
-
哈希计算:
使用哈希函数(如 MurmurHash、CityHash 等)生成一个固定长度的哈希值(通常为 64 位整数)。
假设哈希结果为:0x1A9F3D7B4C2E1856 -
转换为二进制:
将哈希值展开为 64 位二进制串:0001 1010 1001 1111 0011 1101 0111 1011 0100 1100 0010 1110 0001 1000 0101 0110
2. 确定寄存器索引(分桶)
寄存器(也称为“桶”)是 HLL 存储数据的基本单元,数量为 m = 2^b,由参数 b 决定。假设 b = 4,则 m = 2^4 = 16 个寄存器。
- 提取前
b位:
从二进制哈希值的**最高位(最左侧)**开始,提取前 4 位作为寄存器索引:
因此,该元素被分配到寄存器 1(索引从 0 开始)。0001 1010 ... → 前 4 位为 `0001` → 十进制值为 `1`
3. 计算最左侧 1 的位置 p
在剩余的 64 - b = 60 位中,找到第一个出现的 1,并计算其位置:
-
剩余位分析:
去掉前 4 位后,剩余的二进制串为:1010 1001 1111 0011 1101 0111 1011 0100 ... -
前导零计数:
从左侧第一个位开始,连续的 0 的数量为 0(因为第一位就是 1)。
因此,p = 前导零数量 + 1 = 0 + 1 = 1。
4. 更新寄存器值
寄存器初始值为 0。对于当前元素:
- 寄存器索引:1
- p 值:1
更新规则:register[1] = max(register[1], 1) = max(0, 1) = 1。
因此,寄存器 1 的值变为 1。
5. 处理更多元素的示例
假设 HLL 处理了 1000 个不同的字符串,每个元素经过哈希后:
- 元素 A:映射到寄存器 3,p=4 →
register[3] = 4 - 元素 B:映射到寄存器 3,p=2 →
register[3] = max(4, 2) = 4(不变) - 元素 C:映射到寄存器 7,p=5 →
register[7] = 5 - 元素 D:映射到寄存器 7,p=6 →
register[7] = max(5, 6) = 6
最终,部分寄存器的值可能如下:
register[0] = 3, register[1] = 1, register[2] = 2, register[3] = 4,
register[4] = 2, register[5] = 3, register[6] = 0, register[7] = 6, ...
6. 基数计算
当所有元素处理完毕后,使用调和平均数公式计算基数:
-
公式:
基数 ≈ 常数 × m² / (1/R[0] + 1/R[1] + ... + 1/R[m-1])m:寄存器数量(如 16)R[j]:第j个寄存器的值- 常数:0.79402(默认值,根据
m调整)
-
示例计算:
假设m = 16,部分寄存器值为[3, 1, 2, 4, 2, 3, 0, 6, ...],忽略值为 0 的寄存器(实际处理中需特殊处理):调和平均数 = 16² / (1/3 + 1/1 + 1/2 + 1/4 + 1/2 + 1/3 + 1/6 + ...) ≈ 256 / (0.333 + 1 + 0.5 + 0.25 + 0.5 + 0.333 + 0.166 + ...) ≈ 256 / 3.333 ≈ 76.8 基数 ≈ 0.79402 × 76.8 ≈ 60.9 最终结果:floor(60.9) = 60
HLL的原理
看到上面的示例计算过程,你应该会有一个疑问,为什么这个算法是有效的,这其实是源自一种利用概率估计样本数的思想:
- 哈希值均匀分布:如果哈希函数足够好,那么哈希值的二进制位中,前导零的数量越多(即 p 越大),出现的概率越低。
- 最大前导零数量与基数的关系:如果某个寄存器的 p 值很大(如 5),说明 HLL 至少见过 2^5 = 32 个不同的元素(概率上)。通过多个寄存器的最大值组合,可以估计整体基数。
一句话总结就是当一个小概率事件发生时,大概率是已经有了很多的样本,越多的样本就越容易触发越小的概率时间,这也就是我们常说的世界之大无奇不有,林子大了什么鸟都有。我们下面再来详细的解释这个概率思想:
一、哈希值均匀分布:前导零越多,出现概率越低
HLL 的核心前提是哈希函数能产生均匀分布的哈希值。一个“足够好”的哈希函数(如 MD5、SHA 等)会将输入数据映射为近乎随机的二进制串,且二进制中每个位(bit)为 0 或 1 的概率均为 50%,且各个位之间相互独立(无关联)。
基于这种均匀性,我们可以分析“前导零数量”(即二进制串中从最高位开始连续的 0 的个数)的概率:
- 前导零数量为
k意味着:最高位到第k位都是 0,且第k+1位是 1(此时“最左侧 1 的位置”p = k + 1)。 - 例如:若
p=3,则前导零数量为 2(前两位是 0,第三位是 1)。
由于每个位为 0 或 1 的概率独立且均为 50%,“前导零数量为 k”(即 p = k+1)的概率为:
概率 = (1/2)^(k+1)
(前 k 位都是 0 的概率为 (1/2)^k,第 k+1 位是 1 的概率为 1/2,相乘后得到总概率)。
p(最左侧 1 的位置) | 前导零数量 k | 出现概率 |
|---|---|---|
| 1 | 0(最高位是 1) | 1/2^1 = 50% |
| 2 | 1 | 1/2^2 = 25% |
| 3 | 2 | 1/2^3 = 12.5% |
| 4 | 3 | 1/2^4 = 6.25% |
| … | … | … |
p | p-1 | 1/2^p |
显然,p 越大(前导零越多),出现的概率越低。例如:p=5 的概率仅为 1/32 ≈ 3.125%,p=10 的概率更是低至 1/1024 ≈ 0.098%。
二、最大前导零数量与基数的关系:p 越大,见过的元素越多
HLL 通过多个寄存器(桶)记录每个桶中观察到的最大 p 值,再通过这些最大值估计总体的唯一元素数量(基数)。其核心逻辑是:小概率事件(大 p)的发生,暗示样本量(元素数量)足够大。
直观理解:
假设我们只关注一个寄存器(桶),当该寄存器中记录的最大 p 值为 5 时,意味着:
在进入该寄存器的所有元素中,至少有一个元素的 p=5(前导零数量为 4)。
而 p=5 出现的概率仅为 1/32(见上文)。如果见过的元素数量很少(比如少于 32 个),这个小概率事件几乎不可能发生;只有当元素数量足够多(理论上至少 32 个)时,才有可能“撞上”这个低概率事件。
因此,一个寄存器的最大 p 值为 k 时,我们可以推断:进入该寄存器的元素数量至少有 2^k 个(概率意义上)。
多个寄存器的组合:
实际中,HLL 会将哈希值的前 b 位作为寄存器索引(共 m=2^b 个寄存器),每个寄存器对应哈希空间的一个子区域。
- 每个寄存器记录自己区域内观察到的最大
p值; - 整体基数的估计则通过综合所有寄存器的最大
p值计算(公式:基数 ≈ 常数 × m² / 所有寄存器的 1/R[j] 之和,其中R[j]是第j个寄存器的最大p值)。
这种组合利用了“哈希空间均匀划分”的特性:每个寄存器覆盖一部分哈希值,它们的最大 p 值共同反映了整体元素的分布情况,最终通过数学调和平均修正偏差,得到接近真实值的基数估计。
细节
这里你可能还有一个问题,就是为什么不直接使用一个寄存器而是要使用多个寄存器,以及b的值应该如何确定:
一、为什么不使用一个寄存器?
如果仅使用一个寄存器,HLL 的基数估计会严重依赖“所有元素中最大的 p 值”(p 是哈希值中最左侧 1 的位置),但这种方式会导致巨大的误差,原因如下:
1. 单一寄存器的估计方差极大
根据 HLL 的概率直觉:哈希值的前导零数量(p-1)服从几何分布——p 越大(前导零越多),出现的概率越低。例如,p=5(前导零 4 个)的概率是 1/2^5 = 1/32,p=10 的概率是 1/2^10 = 1/1024。
如果只用一个寄存器,最终的基数估计完全依赖这个寄存器记录的最大 p 值(假设为 p_max),估计公式会简化为 ~2^p_max。但这个估计值的随机性极强:
- 即使实际基数很大(比如 100 万),也可能恰好没有元素的
p值很大,导致p_max偏小,估计值远小于实际值; - 反之,即使实际基数很小(比如 100),也可能偶然出现一个
p很大的元素(虽然概率低,但存在可能),导致p_max偏大,估计值远大于实际值。
单一寄存器无法区分“偶然出现的大 p”和“真实的高基数”,导致估计结果极不稳定。
2. 多个寄存器通过“分区降低方差”提高精度
HLL 引入多个寄存器(m 个),本质是将哈希值的空间分区处理:
- 每个寄存器对应哈希值的一个“子空间”(通过哈希值的前
b位确定,m=2^b); - 每个子空间内独立记录该区域中元素的最大
p值。
最终的基数估计是所有寄存器的 p 值的综合结果(通过调和平均计算),而非单一最大值。这种“分区-独立估计-综合”的策略能大幅降低方差:
- 单个寄存器的误差可能较大,但多个寄存器的误差会相互抵消(统计上,独立样本的平均能降低方差);
- 即使某个寄存器因偶然出现大
p而高估,其他寄存器的正常估计会“拉平”整体结果,使最终估计更接近真实值。
二、如何确定寄存器的数量?
寄存器的数量 m 由参数 b 决定(m = 2^b,b 是哈希值中用于确定寄存器索引的前导比特数)。b 的选择需要权衡内存占用和估计精度,具体如下:
1. 寄存器数量与内存的关系
每个寄存器的大小通常为几个比特(用于存储 p 值,p 最大不超过哈希值的位数,例如 64 位哈希中 p 最大为 64,因此每个寄存器只需 6-7 比特)。因此:
- 总内存 =
m × 每个寄存器的比特数。
例如:
- 若
b=10,则m=1024,每个寄存器用 6 比特,总内存 = 1024 × 6 = 6144 比特 ≈ 768 字节; - 若
b=20,则m=1,048,576,总内存 = 1,048,576 × 6 ≈ 786 KB。
b 越大(m 越大),内存占用越高,但精度越高。
2. 寄存器数量与估计精度的关系
HLL 的理论误差公式为 ≈1.04 / sqrt(m)(在理想哈希分布下)。可见:
m越大(b越大),误差越小。
例如:
m=1024(b=10):误差 ≈ 1.04 / 32 ≈ 3.25%;m=1,048,576(b=20):误差 ≈ 1.04 / 1024 ≈ 0.1%。
因此,寄存器数量的选择本质是在可接受的内存成本下,追求足够小的误差:
- 若场景允许 5% 左右的误差(如粗略统计日活用户),
b=10(m=1024)即可,内存仅几百字节; - 若需要 1% 以内的高精度(如金融领域的用户行为统计),则需
b=14(m=16384,误差≈0.8%)或更大的b。
3. 实际应用中的选择
工程中通常根据业务需求的精度要求反推 m:
- 先确定可接受的最大误差(如 2%);
- 根据误差公式
1.04 / sqrt(m) ≤ 误差,计算m ≥ (1.04 / 误差)^2; - 选择满足条件的最小
m(即最小的b,因m=2^b需为 2 的幂)。
例如,若误差要求 ≤ 2%,则 m ≥ (1.04 / 0.02)^2 = 2704,因此选择 b=12(m=4096,误差≈1.6%)。
C++ Primer 任务1 代码实现
基于上面的分析再结合测试代码我们就能理解实际使用是如何调用的:
#pragma once#include <bitset>
#include <memory>
#include <mutex> // NOLINT
#include <string>
#include <utility>
#include <vector>#include "common/util/hash_util.h"/** @brief 位集流的容量。 */
#define BITSET_CAPACITY 64namespace bustub {template <typename KeyType>
class HyperLogLog {/** @brief HLL的常量。 */static constexpr double CONSTANT = 0.79402;public:/** @brief 禁用默认构造函数。 */HyperLogLog() = delete;explicit HyperLogLog(int16_t n_bits);/*** @brief 基数的获取器。** @returns 基数的值*/auto GetCardinality() { return cardinality_; }auto AddElem(KeyType val) -> void;auto ComputeCardinality() -> void;private:/*** @brief 计算给定值的哈希。** @param[in] val - 值* @returns 给定输入值的哈希整数*/inline auto CalculateHash(KeyType val) -> hash_t {Value val_obj;if constexpr (std::is_same<KeyType, std::string>::value) {val_obj = Value(VARCHAR, val);} else {val_obj = Value(BIGINT, val);}return bustub::HashUtil::HashValue(&val_obj);}auto ComputeBinary(const hash_t &hash) const -> std::bitset<BITSET_CAPACITY>;auto PositionOfLeftmostOne(const std::bitset<BITSET_CAPACITY> &bset) const -> uint64_t;/** @brief 基数值。 */size_t cardinality_;/** @todo (学生) 可以添加支持HyperLogLog的数据结构 */
};} // namespace bustub
上面是HLL的头文件,整个HLL是一个类,我们对这个类的使用都是使用public对外提供的函数(也可以说是接口)进行操作, 所以首先会使用HyperLogLog构造函数进行类的初始化,然后调用AddElem向其中添加元素并更新寄存器的值,然后调用ComputeCardinality基于寄存器的值结合公式进行计算,并将结果存储在cardinality_中,最后调用GetCardinality获取前面得到的结果。
按照课程要求,作者不应该公开源代码,所以这里就简单的说一下作者认为的重点,第一个重点是前导零的数量最终一定要加一,这是因为在HLL中,我们要找的其实是第一个1的位置,其计数是从1开始的,并不是0,所以我们其实是通过找前导零的方式间接寻找第一个1所在的位置,所以如果剩余位的第一个数就是1,这时我们得到的前导0的数量为0,这时我们就要加1来得到正确的位置;第二个重点是一定要处理好各种边界情况和数据结构,例如项目要求最终结果应该向下取整;第三个重点是大部分情况下你都会自己添加一些函数和数据结构,它给的并不是完整的,甚至你可以修改原本的代码(但不应该修改与测试代码相关的函数声明或数据结构)。
第0个项目:C++ Primer 任务2
这个任务是完成Presto 的 HLL实现,它采用了一种特殊的密集布局策略,与标准 HLL 的主要区别在于:它统计的是哈希值最右侧连续零的数量,而非左侧。这种设计更适合处理高基数场景,并通过溢出桶机制优化了存储效率。下面这张表格列出了它们的区别:
| 特性 | 标准HLL | Presto的HLL |
|---|---|---|
| 零位统计方向 | 左侧前导零 | 右侧连续零 |
| 存储方式 | 单一寄存器数组 | 密集桶 + 溢出桶 |
| 处理大数值 | 直接存储前导零计数 | 拆分为MSB(溢出桶)和LSB(密集桶) |
| 基数估算公式 | 标准公式 | 需合并两个桶的数据 |
下面是对Presto 的 HLL实现的介绍:
The Presto-specific implementation of HLL data structures has one of two layout formats: sparse or dense. Storage starts off with a sparse layout to save on memory. If the input data structure goes over the prespecified memory limit for the sparse format, Presto automatically switches to the dense layout.
We introduced a sparse layout to ensure an almost exact count in low-cardinality data sets (e.g., number of distinct countries). But if the cardinality is high (e.g., number of distinct users), the dense layout will be what the HLL algorithm will produce as an approximate estimate. The handling of sparse to dense is taken care of automatically by Presto.
Sparse layout stores a set of 32-bit entries/buckets next to one another, sorted in ascending order by bucket index. As new data comes in, Presto checks whether the bucket number already exists. If it does, its value is updated. If the bucket is new, Presto allocates a new 32-bit memory address to hold the value. As more data flows in, the number of buckets may increase above a prespecified memory limit. At that point, Presto switches to a dense layout representation.
Dense layout has a fixed number of buckets and the associated memory is allocated from the beginning. Bucket values are stored as deltas from a baseline value, which is computed as: . The bucket’s values are encoded as a sequence of 4-bit values, as shown in the figure below. Based on the statistical properties of the HLL algorithm, 4-bits is sufficient to encode the majority of the values in a given HLL structure. For deltas greater than 2^4, the remainders are stored in a list of overflow entries.baseline = min(buckets)
上面内容的意思是Presto中针对HLL数据结构的特定实现有两种布局格式:稀疏(sparse)和密集(dense)。存储初始采用稀疏布局以节省内存,当输入的数据结构超过为稀疏格式预设的内存限制时,Presto会自动切换到密集布局。引入稀疏布局是为了确保在低基数数据集中实现近乎精确的计数;而对于高基数数据,HLL算法会采用密集布局来生成近似估计值,且稀疏到密集的转换由Presto自动处理。稀疏布局将一组32位的条目/桶按桶索引升序连续存储,新数据进入时,Presto会检查桶编号是否已存在,若存在则更新其值,若为新桶则分配新的32位内存地址来存储值,当桶的数量超过预设内存限制时,就会切换到密集布局。密集布局从一开始就有固定数量的桶并分配好相关内存,桶的值以相对于基线值(baseline = min(buckets))的差值形式存储,这些值被编码为4位值的序列——根据HLL算法的统计特性,4位足以编码特定HLL结构中的大部分值,而对于大于2^4的差值,其余数则存储在溢出条目列表中。
而我们要完成的实现仅仅是密集布局的实现,所以下面我们只将密集布局,下面是个具体的例子:
前提设定
- 桶数量
m=8(p=3,即2³=8个桶,索引0-7); - 哈希函数输出64位二进制,统计右侧连续零位数量
r(用于计算max_bits); - 密集桶用4位存储
delta(范围0-15),溢出桶存储delta>15时的高3位(MSB),max_bits = baseline + (MSB×16 + LSB)(LSB为密集桶存储的低位,无溢出则MSB=0); - 基数计算公式:
cardinality ≈ α × m² / sum(2^(-max_bits))(m=8时修正系数α≈0.637)。
完整流程
步骤1:初始状态——计算初始baseline、delta及溢出桶状态
系统刚启动,已插入少量元素,8个桶的max_bits(每个桶记录的最大r)如下:
| 桶索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
max_bits | 3 | 5 | 4 | 6 | 3 | 7 | 5 | 4 |
- 计算
baseline:所有max_bits的最小值为3 →baseline=3; - 计算
delta:delta = max_bits - baseline:
| 桶索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
delta | 0 | 2 | 1 | 3 | 0 | 4 | 2 | 1 |
- 溢出桶状态:所有
delta≤15,无需溢出存储 → 溢出桶为空(无键值对)。
步骤2:插入新元素——baseline更新与delta调整
插入一批新元素后,部分桶的max_bits更新:
- 桶0的
max_bits从3→5; - 桶4的
max_bits从3→6;
更新后的max_bits:
| 桶索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
max_bits | 5 | 5 | 4 | 6 | 6 | 7 | 5 | 4 |
- 重新计算
baseline:所有max_bits的最小值为4(桶2和桶7)→baseline=4; - 调整
delta:delta = new_max_bits - new_baseline:
| 桶索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
delta | 1 | 1 | 0 | 2 | 2 | 3 | 1 | 0 |
- 溢出桶状态:所有
delta≤15→ 溢出桶仍为空。
步骤3:插入大量元素——溢出桶首次出现
插入海量元素后,部分桶的max_bits大幅增长:
- 桶3的
max_bits从6→18; - 桶5的
max_bits从7→22;
更新后的max_bits:
| 桶索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
max_bits | 5 | 5 | 4 | 18 | 6 | 22 | 5 | 4 |
- 重新计算
baseline:最小值仍为4(桶2和桶7)→baseline保持4; - 调整
delta并处理溢出:delta = max_bits - 4:
| 桶索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
delta | 1 | 1 | 0 | 14 | 2 | 18 | 1 | 0 |
-
桶3的
delta=14≤15→ 密集桶存储LSB=14(4位二进制1110),无溢出; -
桶5的
delta=18>15→ 拆分存储:LSB=18%16=2(密集桶),MSB=18//16=1(溢出桶); -
溢出桶状态:存储桶5的高位部分 → 溢出桶:
{5:1}(键为桶索引5,值为MSB=1)。
步骤4:整体基数增长——baseline再次更新,溢出桶不变
随着基数持续增长,所有桶的max_bits普遍增加2(整体偏移):
更新后的max_bits:
| 桶索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
max_bits | 7 | 7 | 6 | 20 | 8 | 24 | 7 | 6 |
- 重新计算
baseline:最小值变为6(桶2和桶7)→baseline=6; - 调整
delta:delta = new_max_bits - 6:
| 桶索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
delta | 1 | 1 | 0 | 14 | 2 | 18 | 1 | 0 |
-
桶5的
delta=18仍需拆分 →LSB=2(密集桶),MSB=1(溢出桶); -
溢出桶状态:无变化 → 溢出桶保持
{5:1}。
最终基数计算(基于步骤4的状态)
步骤1:计算每个桶的max_bits
根据max_bits = baseline + (MSB×16 + LSB)(baseline=6,MSB从溢出桶取,无溢出则MSB=0):
| 桶索引 | LSB(密集桶) | MSB(溢出桶) | max_bits计算过程 | 实际max_bits |
|---|---|---|---|---|
| 0 | 1 | 0 | 6 + (0×16 + 1) | 7 |
| 1 | 1 | 0 | 6 + (0×16 + 1) | 7 |
| 2 | 0 | 0 | 6 + (0×16 + 0) | 6 |
| 3 | 14 | 0 | 6 + (0×16 + 14) | 20 |
| 4 | 2 | 0 | 6 + (0×16 + 2) | 8 |
| 5 | 2 | 1 | 6 + (1×16 + 2) | 24 |
| 6 | 1 | 0 | 6 + (0×16 + 1) | 7 |
| 7 | 0 | 0 | 6 + (0×16 + 0) | 6 |
步骤2:计算sum(2^(-max_bits))
对每个桶的2^(-max_bits)求和(忽略极小项):
| 桶索引 | max_bits | 2^(-max_bits)(近似值) |
|---|---|---|
| 0 | 7 | 1/128 ≈0.0078125 |
| 1 | 7 | ≈0.0078125 |
| 2 | 6 | 1/64 ≈0.015625 |
| 3 | 20 | ≈9.5367×10⁻⁷(可忽略) |
| 4 | 8 | 1/256 ≈0.00390625 |
| 5 | 24 | ≈5.9605×10⁻⁸(可忽略) |
| 6 | 7 | ≈0.0078125 |
| 7 | 6 | ≈0.015625 |
总和:0.0078125+0.0078125+0.015625+0.00390625+0.0078125+0.015625≈0.05859375
步骤3:代入公式计算基数
cardinality ≈ 0.637 × 8² / 0.05859375 ≈ 0.637 × 64 / 0.05859375 ≈ 0.637 × 1092 ≈ 696
这里我们还要再额外说一些问题,首先密集布局的实现是基于桶的数量非常多的情况,而我们上面举的例子中桶的数量很少,所以显得对于baseline和delta这两个特点的引入有些多此一举,但实际上,当桶的数量达到数万甚至数十万时,这个增量编码的方案优势就凸显出来了。
要彻底理解这个问题我们要了解这个Presto改进的目标:在超大数据集上高效估算去重元素数量(基数),并极致优化内存使用。其核心原理在于预分配所有 2^p 个桶内存,但通过压缩减少单桶占用,少数例外的值通过溢出桶处理,这使得无论数据大小,内存占用都是固定的。
基于这个理念我们其实能提出两种存储方案:
方案设计对比
| 指标 | 增量编码(Delta Encoding) | 拆分存储(4+3位) |
|---|---|---|
| 存储结构 | 所有桶统一存储 4位 Δ值(Δ = ρ - Baseline) | 所有桶统一存储 4位低位(ρ & 0xF) |
| 溢出机制 | Δ > 15 时存完整 ρ 到溢出列表 | 低位=15 时存 3位高位(ρ >> 4) |
| 重构 ρ 值 | ρ = Baseline + Δ (或查溢出列表) | ρ = (高位 << 4) + 低位 |
| 基线依赖 | 依赖全局最小值 Baseline = min(ρ) | 无全局依赖 |
关键问题:为何拆分方案不如增量编码?
问题1:无法压缩高位共性,浪费空间
- 核心缺陷:
高位相同的ρ值重复存储相同的高3位,无法共享共性。
举例:假设 1000 个桶的ρ=23(二进制00010111):- 增量编码:Baseline 设为
23→ 所有桶的Δ=0→ 仅需存储 4位0 - 拆分方案:
- 低4位 =
0111(7) - 每个桶需额外存储高3位
0001→ 1000 × 3位 = 3000位(375字节)浪费
- 低4位 =
💡 增量编码通过全局
Baseline吸收共性高位,而拆分方案被迫为每个桶单独存高位。 - 增量编码:Baseline 设为
问题2:溢出判定不准确,触发频率过高
- 拆分策略:仅当
低位=15(二进制1111)时触发存储高位。
但ρ=15的桶可能并不需要额外存储(尤其在Baseline接近 15 时)。 - 增量编码优势:
仅当ρ - Baseline > 15时触发溢出 → 溢出概率显著更低。
问题3:无法动态适应分布偏移
- 拆分方案:
ρ值分布偏移时(如从0-15→16-31),所有桶低4位不变,但强制进入“溢出状态” → 每桶需额外存高3位。 - 增量编码:
通过动态调整Baseline适应偏移 →Δ保持小范围 → 仍可存入 4位。
对于增量方案也有两种实现:
| 特性 | Presto实现简化版 | Presto实现 |
|---|---|---|
| 核心思想 | 基于全局最小值动态压缩 | 对增量值进行算术分解 |
| 主存储结构 | 固定位宽数组 (每桶 4位) | 固定位宽数组 (每桶 4位) |
| 存储内容 | Δ = ρ - B(若 Δ≤15 直接存储) | Δ % 16(低4位) |
| 溢出标记 | 存 15(二进制 1111) | 当 Δ ≥ 16 时强制占用主存储位 |
| 溢出结构 | 独立列表(存储完整的 (桶索引, ρ)) | 独立位域(存储 Δ // 16,每项 3位) |
| 溢出触发条件 | Δ > 15 | Δ ≥ 16(含 Δ=16) |
| 重构逻辑 | if 主存值 != 15: | ρ = B + (MSB << 4) + LSB |
| Δ=18 的存储示例 | ![主存] 1111(15)![溢出] ρ=18(完整值) | ![主存] 0010(2 = 18%16)![溢出] 001(1 = 18//16) |
可以看出简化版的实现操作更加直观简洁,但代价在于对于溢出桶来说需要存储完整值,这代表着需要更大的内存占用,显然从Presto的改进目标来看,是不符合极致的内存占用的,因此在实际Presto的应用中,并不会使用简化版的实现,但是简化版的实现可以更改一下,例如溢出桶可以存储实际的哈希值,这样需要的空间会很大,但是可以用于检测哈希冲突。
C++ Primer 任务2 代码实现
//===----------------------------------------------------------------------===//
//
// BusTub
//
// hyperloglog_presto.h
//
// 标识符: src/include/primer/hyperloglog_presto.h
//
// 版权所有 (c) 2015-2025, 卡内基梅隆大学数据库组
//
//===----------------------------------------------------------------------===//#pragma once#include <bitset>
#include <memory>
#include <mutex> // NOLINT
#include <sstream>
#include <string>
#include <unordered_map>
#include <utility>
#include <vector>#include "common/util/hash_util.h"/** @brief 密集桶大小。 */
#define DENSE_BUCKET_SIZE 4
/** @brief 溢出桶大小。 */
#define OVERFLOW_BUCKET_SIZE 3/** @brief 总桶大小。 */
#define TOTAL_BUCKET_SIZE (DENSE_BUCKET_SIZE + OVERFLOW_BUCKET_SIZE)namespace bustub {template <typename KeyType>
class HyperLogLogPresto {/*** 说明: 测试框架将使用GetDenseBucket和GetOverflow函数,* 因此不应删除。必须使用dense_bucket_数据结构。*//** @brief HLL的常量。 */static constexpr double CONSTANT = 0.79402;public:/** @brief 禁用默认构造函数。 */HyperLogLogPresto() = delete;explicit HyperLogLogPresto(int16_t n_leading_bits);/** @brief 返回dense_bucket_数据结构。 */auto GetDenseBucket() const -> std::vector<std::bitset<DENSE_BUCKET_SIZE>> { return dense_bucket_; }/** @brief 返回指定索引处的溢出桶。 */auto GetOverflowBucketofIndex(uint16_t idx) { return overflow_bucket_[idx]; }/** @brief 返回集合的基数。 */auto GetCardinality() const -> uint64_t { return cardinality_; }auto AddElem(KeyType val) -> void;auto ComputeCardinality() -> void;private:/** @brief 计算哈希值。** @param[in] val** @returns 哈希值*/inline auto CalculateHash(KeyType val) -> hash_t {Value val_obj;if constexpr (std::is_same<KeyType, std::string>::value) {val_obj = Value(VARCHAR, val);return bustub::HashUtil::HashValue(&val_obj);}if constexpr (std::is_same<KeyType, int64_t>::value) {return static_cast<hash_t>(val);}return 0;}/** @brief 存储密集桶(也称为寄存器)的结构。 */std::vector<std::bitset<DENSE_BUCKET_SIZE>> dense_bucket_;/** @brief 存储溢出桶的结构。 */std::unordered_map<uint16_t, std::bitset<OVERFLOW_BUCKET_SIZE>> overflow_bucket_;/** @brief 存储基数的值 */uint64_t cardinality_;// TODO(学生) - 根据需要可以添加更多数据结构
};} // namespace bustub
//===----------------------------------------------------------------------===//
//
// BusTub
//
// hyperloglog_presto.cpp
//
// 标识符: src/primer/hyperloglog_presto.cpp
//
// 版权所有 (c) 2015-2025, 卡内基梅隆大学数据库组
//
//===----------------------------------------------------------------------===//#include "primer/hyperloglog_presto.h"namespace bustub {/** @brief 参数化构造函数。 */
template <typename KeyType>
HyperLogLogPresto<KeyType>::HyperLogLogPresto(int16_t n_leading_bits) : cardinality_(0) {}/** @brief 向HLL中添加元素以进行基数计算。 */
template <typename KeyType>
auto HyperLogLogPresto<KeyType>::AddElem(KeyType val) -> void {/** @TODO(学生) 实现此函数! */
}/** @brief 计算基数的函数。 */
template <typename T>
auto HyperLogLogPresto<T>::ComputeCardinality() -> void {/** @TODO(学生) 实现此函数! */
}// 显式实例化模板类
template class HyperLogLogPresto<int64_t>;
template class HyperLogLogPresto<std::string>;} // namespace bustub
从代码我们能看出低位寄存器和高位寄存器的大小都是固定的,与前面不同的是,Presto HLL的寄存器(桶)此时存的不再是十进制的值,而是二进制的值,与之同时改变的还有存放值的计算方法以及最后的基数计算方法,我们主要改变的也是这里,其他的都相差不大。不过这里有个重点,任务2要求我们要将哈希值转换为 64 位二进制,然后计算连续零 (LSB),我们从头文件的哈希计算函数可以看出相对于前面对于整数类型仅仅是做了类型转换,所以这个哈希计算函数是不能修改的。
还有一个重点在于密集桶和溢出桶的数据结构选型:
- 密集桶使用vector的原因
密集桶的核心特性是固定数量、连续索引、高频随机访问,而vector的特性完美适配这些需求:
(1)固定数量与连续索引:根据前文,密集布局 “有固定数量的桶(fixed number of buckets)”,每个桶对应一个明确的索引(0 到 N-1,N 为固定值)。vector是连续内存的线性容器,其元素按索引顺序存储,索引与桶的位置直接对应(如vector[i]就是第 i 个桶的值),可以通过索引O (1) 时间随机访问,效率极高。
(2)内存紧凑与缓存友好:vector的连续内存布局能充分利用 CPU 缓存,减少缓存未命中(cache miss)。密集桶的 4 位编码值存储密集,连续访问时缓存效率更高,适合高频读写操作(如更新桶值、计算基线值等)。
(3)无需动态增删:密集桶的数量从一开始就固定(内存预分配),不会因为数据输入而增加或减少,vector的 “预分配固定大小” 特性避免了动态扩容的开销,也无需额外空间存储键(索引可通过位置直接推导)。 - 溢出桶使用unordered_map的原因
溢出桶的核心特性是数量动态、索引稀疏、高频键值查找,而unordered_map(哈希表)的特性更适配这些需求:
(1)动态数量与稀疏索引:溢出桶存储的是 “delta 大于 2^4 的余数”,这类条目是少数(根据 HLL 的统计特性,多数值可被 4 位编码,溢出是例外),且其对应的桶索引不连续、数量不固定(随输入数据动态变化)。unordered_map无需预分配固定内存,可动态插入 / 删除键值对(桶索引→溢出值),避免内存浪费。
(2)高效的键值查找:溢出桶需要频繁检查 “某个桶索引是否存在溢出值”(如新增数据时判断是否需存入溢出桶),unordered_map通过哈希函数将桶索引映射到存储位置,平均查找、插入、删除时间复杂度为 O (1),远优于vector(若用 vector 存储稀疏索引,查找需遍历,时间复杂度 O (N))。
(3)键值对存储的天然适配:溢出桶的本质是 “桶索引→溢出值” 的映射关系(只有部分索引有溢出值),unordered_map的键值对结构直接对应这种映射,无需额外逻辑维护索引与值的关联。
这里代码的测试有两个重点,分别是PrestoCase1和PrestoCase2。PrestoCase1需要注意的是如果你的baseline不是0的话后半部分你的代码将会报错,这个目前作者并不知道为什么会这么出测试;PrestoCase2需要注意的是初始化桶的数量应该为1,或者确保桶中索引为0的值为0,不应该为空桶。
C++ Primer代码测试
以下是每个测试目的的精简总结表格:
| 测试名称 | 测试目的 |
|---|---|
HyperLogLogTest.BasicTest1 | 验证HLL在基本场景下(字符串元素、存在重复项)的基数估计值稳定性和准确性。 |
HyperLogLogTest.BasicTest2 | 测试HLL对整数(正负值)的处理能力,验证重复元素对基数估计的影响。 |
HyperLogLogTest.EdgeTest1 | 检测当输入无效精度(负值)时,HLL是否能安全退化(基数保持为0)。 |
HyperLogLogTest.EdgeTest2 | 验证极低精度(精度=0)下的HLL行为,展示精度对估计误差的显著影响及负数的正确处理。 |
HyperLogLogTest.BasicParallelTest | 测试HLL在多线程并发添加元素(包括相同和不同值)时的线程安全性和基数一致性。 |
HyperLogLogTest.ParallelTest1 | 验证高精度模式(精度=14)下的并发性能,检测大量线程添加部分不同元素时基数估计的准确性变化。 |
HyperLogLogTest.PrestoBasicTest1 | 验证Presto变体HLL对字符串的基本处理能力(基数估计逻辑与标准HLL不同)。 |
HyperLogLogTest.PrestoCase1 | 深入测试Presto变体对特定整数(如大数/边界值)的处理,检查内部状态(桶/溢出桶)与基数估计的同步更新。 |
HyperLogLogTest.PrestoCase2 | 测试Presto变体在低精度(精度=0)下的行为,重点验证内部状态更新逻辑的正确性。 |
HyperLogLogTest.PrestoEdgeCase | 检测Presto变体在无效精度(负值)输入时的鲁棒性(安全退化,基数保持0)。 |
关键特征说明:
- 标准HLL测试(BasicTest/EdgeTest):验证基数估计的核心算法
- 并发测试(ParallelTest):检测线程安全性和并发一致性
- Presto变体测试:聚焦特定优化的内部状态管理(桶/溢出桶)
- 边缘测试(EdgeTest):检验极端/无效输入下的鲁棒性
确保从测试名称中删除 DISABLED_ 前缀,否则它们将无法运行,然后向前面一样执行剩余的测试即可,如果你的结果如下,就代表你已经通过全部测试,需要注意的是代码中提供的测试只是将用于评估和评分项目的所有测试的子集,所以并不一定代表你能通过Gradescope的全部测试:
然后我们在build目录中执行下面的代码,这将检查您的语法并自动更正:
$ make format
$ make check-clang-tidy-p0
确保一切无误后执行make submit-p0,这将在根目录创建一个名为project0-submission.zip的文件,我们将这个文件上传到Gradescope后即可,如果一切正常你将看到下面这样的测试报告:
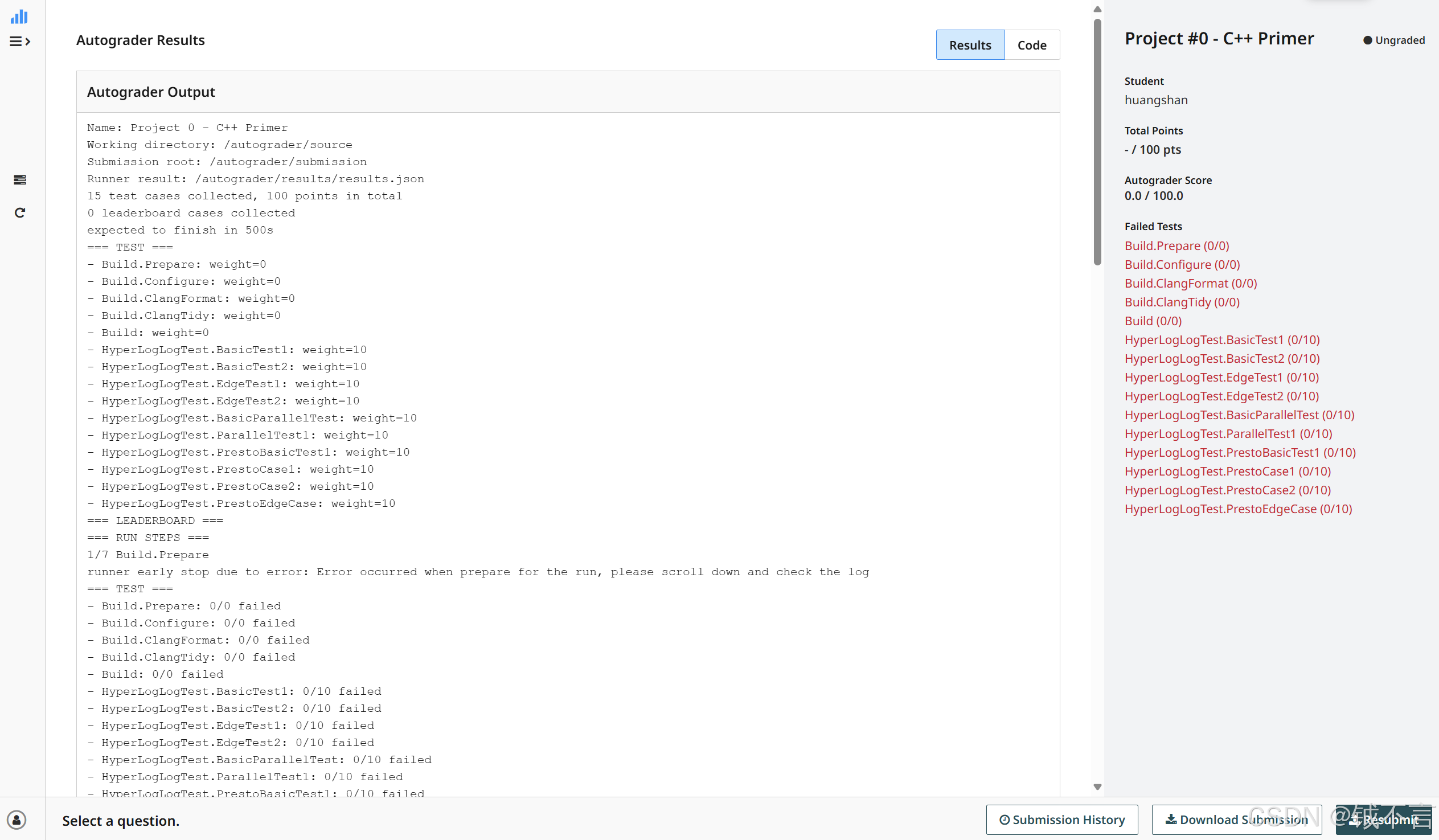
总结
项目0到此结束,当你能独立完成这个项目,说明你已经算是正式入门C++了,C++并不止语法,除此之外作者在了解到这个算法时,也是惊叹于这个算法实现的巧妙。
