算法题打卡力扣第1004. 最大连续1的个数 III(mid)
文章目录
- 题目描述
- 解法一:滑动窗口
题目描述
解法一:滑动窗口
这道题的题意可以转换为:找到一个最长的子数组,这个子数组里最多包含k个0.
为什么可以这样转换呢?因为题目允许我们把 k 个 0 变成 1。如果我们找到了一个子数组,它里面恰好有 k 个 0,那么我们把这些 0 全都变成 1 之后,整个子数组就都是 1 了。这个子数组的长度,就是我们能得到的连续 1 的长度。
对于这类 “寻找满足某个条件的最长连续子数组” 的问题,滑动窗口 是最常用也是最高效的解法。
滑动窗口的运作方式:
我们可以把滑动窗口想象成一个在数组上移动的 “框框”。这个框框的左边界和右边界由两个指针 left 和 right 来定义。
- 窗口的扩张 (right 指针移动):
我们让 right 指针不断地向右移动,把新的元素包含进窗口里。
每当 right 指针遇到一个 0,我们就记录下来,表示我们使用了一次翻转的机会。 - 窗口的收缩 (left 指针移动):
在窗口扩张的过程中,我们可能会遇到窗口内的 0 的数量超过了 k 的情况。
这个时候,说明当前的窗口已经不满足 “最多包含 k 个 0” 的条件了。为了让窗口重新变得 “合法”,我们必须收缩窗口的左边界。
我们让 left 指针向右移动。
如果移出的 nums[left] 恰好是一个 0,那就意味着我们归还了一次翻转的机会。
left 指针持续向右移动,直到窗口内的 0 的数量再次小于或等于 k,窗口就重新合法了。 - 记录最大长度:
在整个过程中(每次 right 指针移动后),窗口的宽度 right - left + 1 都是一个潜在的答案。
我们只需要在循环中不断更新和维护这个最大宽度即可。
算法步骤拆解
初始化两个指针 left = 0, right = 0。 初始化一个变量 zeros 用来记录当前窗口内 0 的数量,zeros = 0。
初始化一个变量 maxLength 用来记录结果,maxLength = 0。
开始一个循环,让 right 指针从 0 遍历到数组末尾:
a. 将 nums[right] 元素纳入窗口。如果 nums[right] 是 0,则 zeros++。
b. 检查窗口合法性:进入一个while 循环,判断 zeros 是否大于 k。
- 如果 zeros > k,说明窗口不合法,需要收缩。
- 检查即将移出窗口的 nums[left]。如果 nums[left] 是 0,则 zeros–(归还了一次机会)。
- left++,将左边界向右移动。
- 这个 while 循环会一直执行,直到 zeros <= k,窗口重新合法。
c. 更新结果:此时的窗口 ([left, right]) 是合法的。我们计算当前窗口的长度 right - left + 1,并更新 maxLength = max(maxLength, right - left + 1)。
d. right++,继续扩张窗口。
right 指针遍历完整个数组后,maxLength 就是最终答案。
实现代码
class Solution {
public:int longestOnes(vector<int>& nums, int k) {int n = nums.size();int left = 0,right = 0;int zeros = 0;int maxlength = 0;for(right = 0;right<n;right++){if(nums[right]==0){zeros++;}while(zeros>k){if(nums[left]==0){zeros--;}left++;}int len = right-left+1;maxlength = max(len,maxlength);}return maxlength;}
};
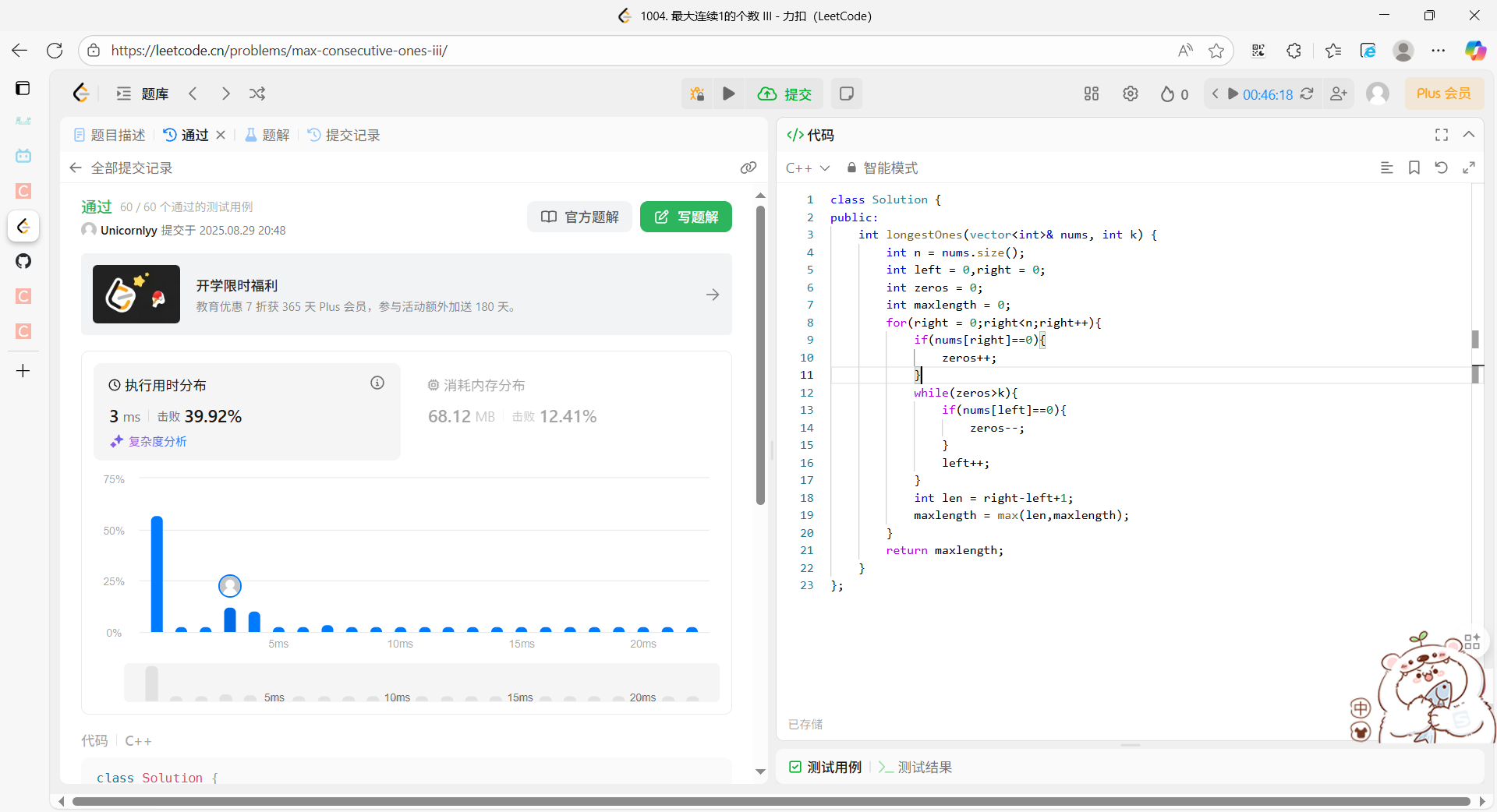
执行结果:
复杂度分析:
时间复杂度:O(n)
空间复杂度:O(1)
