自然语言处理深层语义分析中公理化体系的可行性、挑战与前沿进展

摘要

随着自然语言处理（NLP）技术向更深层次的语义理解迈进，以Transformer架构为核心的连接主义模型（如BERT、GPT系列）虽在众多任务中取得了卓越成就 但其“黑箱”特性、逻辑一致性缺失以及对海量数据的依赖等固有缺陷日益凸显 。为了增强模型的逻辑推理能力、可解释性和可靠性，学界和业界正重新审视符号主义方法的价值。本报告旨在深入探讨将公理化体系（Axiomatic Systems）引入深层语义分析的理论可行性、关键技术、面临的挑战及截至2025年的发展现状。研究发现，公理化体系并非要取代深度学习模型，而是以“神经-符号”混合架构（Neuro-Symbolic AI）的形式与之融合，这已成为该领域最前沿和最具潜力的发展方向 。然而，尽管理论前景广阔，该领域在标准化工具、通用性能基准和规模化商业应用方面仍处于早期探索阶段。

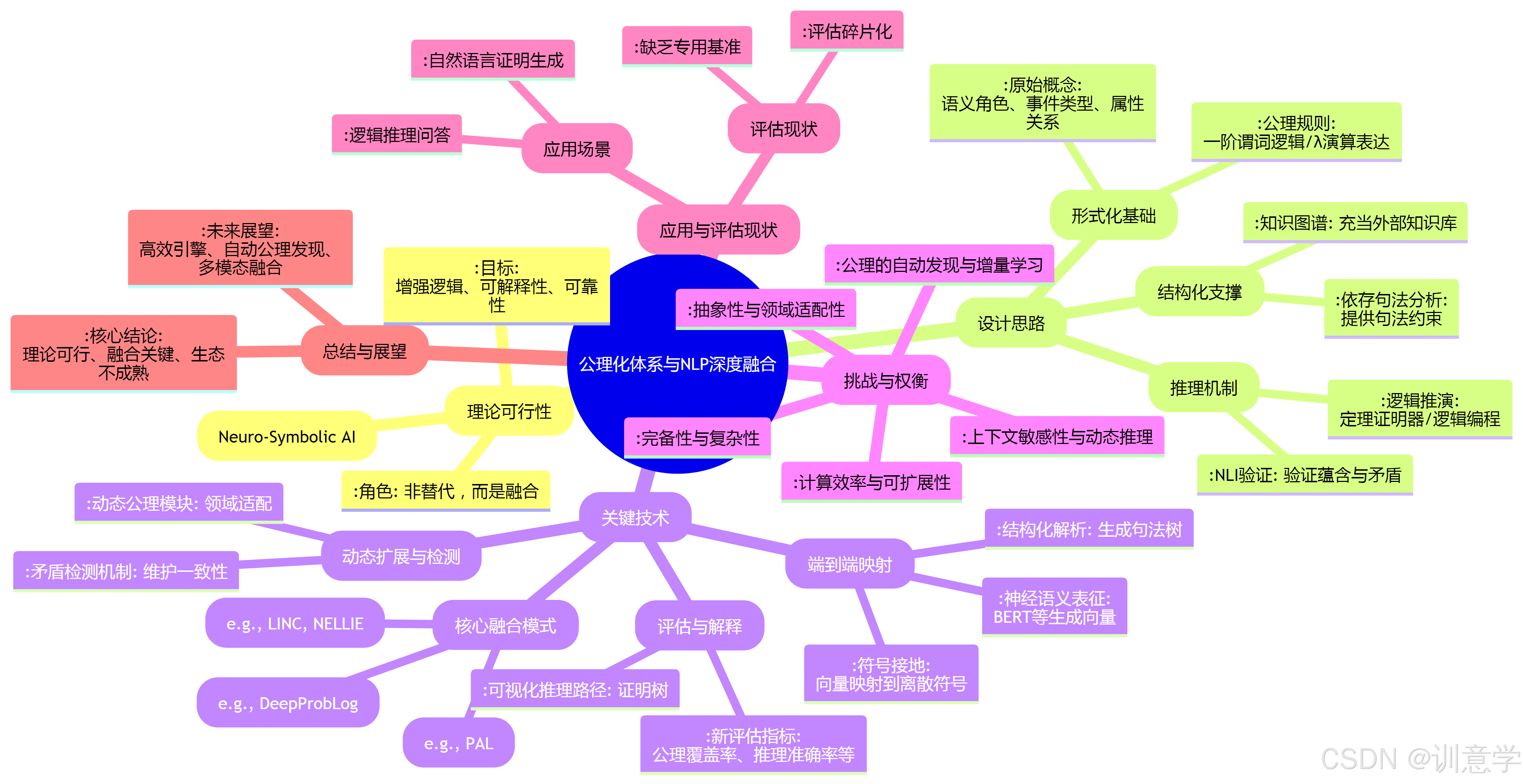
一、 公理模型在深层语义分析中的设计思路

将公理化体系融入深层语义分析，其核心目标是为非结构化的自然语言赋予形式化的逻辑结构，从而实现精确、可解释的语义推导。这一设计思路建立在一个分层的、从具体到抽象的语义表示和推理框架之上。

1.1 形式化基础：原始概念与公理规则

公理化体系的起点是将复杂的语言现象分解为一系列基础的、不可再分的 原始概念（Primitives）。这些概念可以是：

• 语义角色：如“施事者（Agent）”、“受事者（Patient）”、“工具（Instrument）”等。
• 事件类型：如“交易（Transaction）”、“移动（Movement）”、“创造（Creation）”等。
• 实体属性与关系：如“颜色（Color）”、“位置（Location）”、“拥有（has_a）”等。

在定义了原始概念后，系统通过一系列 公理规则（Axioms） 来描述这些概念之间的恒定关系。这些规则通常借鉴数理逻辑的形式化语言，如一阶谓词逻辑（First-Order Logic）或λ演算进行表达 。例如：

• 公理1（动作关系） ：∀X, Y, E (Event(E, '购买') ∧ Agent(E, X) ∧ Patient(E, Y) → Action_Relation(X, Y))，意即“若事件E是‘购买’，X是施事者，Y是受事者，则X与Y之间存在一种动作关系”。
• 公理2（属性继承） ：∀X, Y (is_a(X, Y) ∧ has_property(Y, P) → has_property(X, P))，意即“若X是Y的一种，且Y具有属性P，则X也具有属性P”。

这种形式化的表达方式，如中提到的语义表达式 answer(river(loc_2(stateid('colorado'))))，正是通过谓词和函数的嵌套组合来精确描述实体及其关系的典范。

1.2 结构化支撑：依存句法与知识图谱

公理的实施离不开对句子结构和背景知识的理解。

• 依存句法分析（Dependency Parsing） ：为公理模型提供了至关重要的句法约束。句法树中的主谓宾（nsubj-verb-dobj）结构可以被直接映射为“施事-事件-受事”的语义框架，成为应用公理规则的结构化输入。这解决了如何在连续文本流中定位公理所需变量的问题。
• 知识图谱（Knowledge Graphs） ：扮演了公理模型“外部知识库”的角色 。知识图谱中存储的大量事实（如“马云 创始人 阿里巴巴”）可被视为已经实例化的公理，或作为验证公理推理结果的“世界模型”。例如，“创始人-公司”的关系可以在知识图谱中被公理化定义为 Founder(X, Y) → Person(X) ∧ Organization(Y)，从而为实体类型检查提供依据。

1.3 推理机制：逻辑推演与NLI验证

拥有了公理和结构化输入后，系统通过逻辑推理引擎进行语义推导。

• 经典逻辑推理：如 分离规则（Modus Ponens） 和 三段论（Hypothetical Syllogism） 是最基础的推导范式。例如，若系统已知“A创立了B”（事实）和“创立者必须是人”（公理），则可推断出“A是人”。现代神经-符号系统常将更复杂的 定理证明器（Theorem Provers） （如Isabelle, Coq, Lean）或逻辑编程引擎（如Prolog）作为其符号推理核心 。
• 自然语言推理（NLI）的整合：NLI任务（判断“前提”与“假设”之间的蕴含、矛盾或中立关系）为公理系统提供了一种独特的验证机制。公理可以被视为一种强蕴含关系。因此，可以利用NLI模型来判断一段文本是否与已知的公理集合相符，或检测两段陈述是否因违反同一条公理而构成矛盾 。

二、 关键技术实现要点：神经-符号的融合

截至2025年，业界普遍认识到，纯符号主义的公理系统过于脆弱和僵化，无法处理自然语言的歧义性和多样性。因此，将公理系统与深度学习模型相融合的神经-符号方法成为实现这一构想的主流技术路径 。其核心在于利用神经网络的感知和表征能力，为符号系统的形式化推理提供高质量的输入和引导。

2.1 词汇-句法-语义的端到端映射

此过程旨在将原始文本信号转化为符号系统可以处理的逻辑形式。

1. 神经语义表征：首先，利用预训练语言模型（如BERT）生成富含上下文信息的词向量和句子向量 。这些向量成为语义的分布式表示。
2. 符号接地（Symbol Grounding） ：接着，系统需要将这些连续的向量“接地”到离散的符号上。例如，通过一个分类器或注意力模块，将句子中的某个词或短语的向量映射到预定义的谓词（如is_a）或实体（如马云）。
3. 结构化解析：利用神经依存句法分析器等工具，生成句子的句法结构树，为逻辑形式的构建提供骨架。整个过程旨在将“词嵌入 → 句法树 → 逻辑表达式”的映射尽可能自动化和精准化。

2.2 符号主义与连接主义的核心融合模式

神经-符号的融合并非单一模式，而是呈现出多种技术形态：

• 神经模型作为符号生成器：这种模式利用大型语言模型（LLM）的生成能力。例如， Program-Aided Language Models (PAL) 等方法让LLM在面对需要精确计算或逻辑推理的问题时，不直接生成答案，而是生成一段可执行的代码（如Python）或逻辑表达式，然后交由外部的符号解释器（如代码执行环境或定理证明器）来求解，从而保证结果的精确性 。
• 神经模型作为符号引导器：在此模式下，神经网络负责在庞大的搜索空间中为符号推理引擎提供启发式指导。例如，研究项目LINC结合了语言模型和一阶逻辑证明器，语言模型用于预测哪些公理或事实最有可能用于构建当前目标的证明，从而显著减少符号推理的搜索空间，提升效率 。类似地，NELLIE系统利用神经语言模型引导生成过程，构建可解释的证明树来回答问题 。
• 端到端可微框架：这类方法试图将逻辑规则直接嵌入到神经网络的计算图中，使其成为一个整体可微分的系统。例如，DeepProbLog将概率逻辑编程语言与深度学习结合，允许模型同时学习神经参数和逻辑规则的概率 。这种方法理论上可以实现真正的端到端学习，但通常对逻辑表达的形式有较强限制。

2.3 动态公理扩展与矛盾检测

为适应不同场景，公理系统必须具备灵活性。

• 动态公理模块：针对特定领域（如医疗、法律），可以设计可插拔的公理模块。在处理医疗文本时，加载关于“药物相互作用”、“症状与疾病关系”的公理集；在处理法律文书时，则加载关于“合同要素”、“法律责任主体”的公理集。这种设计避免了单一庞大公理集的复杂性和推理效率问题。
• 矛盾检测机制：公理是实施矛盾检测的天然工具。通过定义互斥关系（如 ∀X, is_antibiotic(X) → ¬is_antiviral(X)），系统可以在语义分析过程中实时检测逻辑谬误，这对于事实核查、对话系统一致性维护等应用至关重要，也是当前LLM面临的一大挑战 。

2.4 可解释性工具与量化评估指标

提升透明度是引入公理系统的核心动机之一。

• 可视化推理路径：一个理想的系统应能将其推理过程可视化。例如，将推导所用的公理、中间结论与原始句子的依存树叠加展示，形成一个清晰的“证明树” ，让用户理解模型为何得出某个结论。
• 设计新的评估指标：传统的黑箱模型评估指标（如准确率、F1值）无法衡量模型的逻辑一致性或可解释性。学界正在探讨新的评估体系 ，尽管尚未形成统一标准。可以提出的新指标包括：
  • 公理覆盖率（Axiom Coverage） ：评估模型在测试集中能够成功应用公理的比例。
  • 推理准确率（Inference Accuracy） ：在需要多步推理才能得出答案的数据集上，评估模型最终结论的正确率。
  • 事实一致性得分（Factual Consistency Score） ：评估模型生成的文本是否与其内部知识库或已知公理集相矛盾。
    然而，截至2025年9月，搜索结果表明，目前尚无专门针对NLP公理系统的标准化基准数据集和排行榜 , Query: 2025年公理系统在NLP中的性能基准测试和实际应用案例研究?)。评估大多仍在通用的推理数据集或NLI任务上进行 。

三、 设计注意事项与核心挑战

将公理化体系付诸实践并非易事，需要平衡多个维度的复杂性，并克服理论与工程上的诸多挑战。

3.1 抽象性与领域适配性的权衡

公理的设计需要在通用性与具体性之间找到平衡点。过于抽象的公理（如 Thing(X) → Exists(X)）虽然普适，但信息量低，实际效用有限。而过于具体的公理（如针对某个特定公司内部业务逻辑的规则）则缺乏泛化能力。一个良好的设计是将核心、稳定的公理（如时间和空间的基本逻辑）作为系统内核，而将易变的、领域特定的公理作为可配置的外部模块。

3.2 公理集的完备性与复杂性

构建一个既能覆盖足够语义现象（完备性）又不会导致组合爆炸（复杂性）的“最小公理集”是一个巨大的挑战。公理的数量和复杂性直接影响推理引擎的计算效率 。根据哥德尔不完备定理的启示，任何足够强大的形式系统都可能存在无法证明或证伪的命题，这意味着追求绝对完备的公理集在理论上是不可行的。因此，实践中更应关注在特定任务领域内构建“足够好”的公理集。

3.3 上下文敏感性与动态推理

纯符号系统的一大弱点是其上下文不敏感性。例如，谓词“打开”在“打开门”和“打开文件”中触发的物理和数字世界的语义后果截然不同。这正是深度学习模型的优势所在。一个成功的混合系统必须能够利用神经网络（如注意力机制）对上下文的深刻理解，来动态地选择、实例化或调整将要应用的公理规则 。

3.4 计算效率与可扩展性

符号推理，尤其是基于一阶逻辑的定理证明，其计算复杂度极高，很多情况下是不可判定或NP难问题。这使得纯符号方法难以应用于需要实时响应的大规模NLP任务。神经-符号方法通过神经网络的启发式引导来缓解这一问题 ，但效率仍是关键瓶颈。此外，随着知识的增长，如何高效地管理和索引数以万计的公理规则，并保证系统性能不发生显著衰减，是工程上必须解决的难题。

3.5 公理的自动发现与增量学习

手动定义和维护一个大规模的公理集成本高昂且容易出错。因此，如何让系统从海量文本数据中自动发现和学习新的公理或规则，是一个极具吸引力但又充满挑战的研究方向。这需要结合关联规则挖掘、因果推断  等技术，从数据中归纳出潜在的、稳定的模式，并将其形式化为新的候选公理。

四、 实际应用与性能评估现状

尽管理论探讨十分活跃，但截至2025年，公理化体系在NLP中的规模化商业应用案例仍然罕见。其应用主要体现在学术界的研究原型和概念验证系统中。

4.1 应用场景示例：研究原型

• 逻辑推理问答：输入一个复杂问题，如：“创立了阿里巴巴并且出生在杭州的人是谁？”

  1. 神经模块：LLM首先将问题解析为结构化的查询意图，识别出 Founder(X, '阿里巴巴') 和 Born_in(X, '杭州') 这两个核心语义片段。
  2. 符号模块：推理引擎利用公理 Founder(X, Y) → Person(X) ∧ Organization(Y) 和 Born_in(X, Z) → Person(X) ∧ Location(Z) 进行类型约束和推导。
  3. 知识库交互：系统在知识图谱中查询同时满足这两个条件的实体 X。
  4. 结果生成：最终定位到实体“马云”并生成答案。
     这个过程在 NELLIE  或类似框架中有所体现，其关键优势是能够生成“因为...所以...”式的可解释推理路径。

• 自然语言证明生成：如 ProofWriter 项目 ，模型能够读取以自然语言陈述的事实和规则，然后生成一个同样是自然语言形式的、逻辑严谨的证明过程，来回答某个假设是否成立。

4.2 性能评估现状：缺乏专用基准

如前文所述，当前领域的一大短板是缺乏专门用于评估NLP公理化系统或神经-符号系统逻辑推理能力的标准化基准。

• 评估方式：研究者通常在现有的、包含逻辑推理元素的NLP数据集上进行评测，如部分NLI数据集、常识问答（CommonsenseQA）和数学推理数据集（GSM8K）等 。
• 性能指标：使用的指标多为任务本身的准确率 。例如，一个神经-符号模型如果在需要逻辑推理的子集上准确率显著高于纯神经模型，则被认为是有效的。
• 现状总结：根据2025年至今的搜索结果，没有发现任何被广泛接受的、名为“公理系统性能基准”的测试集或排行榜。评估方法和数据集的碎片化，使得跨研究比较不同神经-符号架构的真实推理能力变得非常困难。

五、 总结与展望

将公理化体系引入深层语义分析，是解决当前主流深度学习模型在可解释性、逻辑一致性和事实可靠性方面缺陷的一条重要路径。截至2025年，这一方向的最佳实践并非回归纯粹的符号主义，而是探索以形式化逻辑为骨架、以深度神经网络为感知和认知引擎的神经-符号混合架构。

核心结论：

1. 理论可行，实践复杂：设计思路清晰，即通过分层映射将语言转化为逻辑形式并进行推理，但在公理集构建、上下文处理和计算效率上面临巨大挑战。
2. 融合是关键：神经-符号AI是当前最前沿的实现范式，它利用神经网络的灵活性来克服符号系统的僵化，同时借助符号系统的严谨性来规范神经网络的“自由发挥”。LINC、NELLIE等研究原型展示了这一融合的潜力。
3. 生态尚不成熟：该领域仍处于研究探索阶段。缺乏成熟的开源工具链、标准化的性能基准和大规模的商业应用是其发展的主要制约因素。

未来展望：
未来，随着大模型能力的进一步增强，以及对模型可靠性、安全性和透明度要求的日益提高，神经-符号方法的研究热度将持续升温。我们预期在以下几个方面将出现突破：

• 更高效的推理引擎：结合图神经网络等技术，开发能处理大规模公理集的高效推理算法。
• 自动化公理发现：利用小样本学习、元学习等技术，让模型能从少量数据中归纳和学习新的规则。
• 多模态融合：将公理化推理扩展到包含图像、视频的多模态语义理解中，实现对物理世界更深层次的认知。

总之，公理化体系为NLP的未来发展提供了一个回归逻辑与常识的重要视角。虽然前路漫漫，但其在构建真正可信、可解释、有智慧的AI系统方面所蕴含的巨大潜力，值得我们持续投入和探索。

以下是一个简化的代码示例，展示了神经-符号混合架构中，如何利用预训练模型进行初步处理，并为符号推理做准备（基于PyTorch和概念性逻辑编程）：

import torch
from transformers import AutoTokenizer, AutoModel
import numpy as np# 1. 神经感知：使用预训练语言模型获取上下文表示
model_name = "bert-base-uncased"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModel.from_pretrained(model_name)text = "The CEO founded the company in Seattle."
inputs = tokenizer(text, return_tensors="pt", padding=True, truncation=True)
with torch.no_grad():outputs = model(**inputs)word_embeddings = outputs.last_hidden_state # 富含上下文信息的词向量# 2. 符号接地（简化示例）：将神经表征映射到预定义概念
# 假设我们有一个简单的概念分类器（需要单独训练）
def concept_classifier(word_embedding):# 这里是一个简化的示意，实际应用是复杂的多分类或序列标注问题# 返回可能的概念标签，例如 'PERSON', 'ACTION', 'LOCATION'concepts = ['PERSON', 'ACTION', 'LOCATION', 'ORGANIZATION', 'OTHER']# 使用一个简单的线性层进行演示（权重需通过训练获得）classifier_weights = torch.randn(768, len(concepts)) # 假设嵌入维度是768scores = torch.matmul(word_embedding, classifier_weights)predicted_idx = torch.argmax(scores, dim=-1)return concepts[predicted_idx]# 对每个词元（token）进行分类（跳过特殊标记）
tokens = tokenizer.convert_ids_to_tokens(inputs['input_ids'][0])
identified_concepts = []
for i, token in enumerate(tokens):if token not in ['[CLS]', '[SEP]', '[PAD]']:concept = concept_classifier(word_embeddings[0, i])identified_concepts.append((token, concept))print("Identified tokens and concepts:", identified_concepts)# 3. 结构化解析（通常使用专用解析器，如StanfordNLP, spaCy）
# 假设我们得到了依存关系，这里省略具体解析过程
# 解析结果可能包含：('founded', 'ROOT'), ('CEO', 'nsubj'), ('company', 'dobj'), ('Seattle', 'nmod:in')# 4. 逻辑形式构建与推理（概念性示例）
# 基于上述结果，可以尝试应用公理。
# 例如，公理: ∀X, Y, Z (Action(X, 'found') ∧ Agent(X, Y) ∧ Patient(X, Z) → Founder(Y, Z))
# 识别出 Action: founded, Agent: CEO (PERSON), Patient: company (ORGANIZATION)
# 可推断出: Founder(CEO, company)# 5. 知识库交互验证（概念性）
# 查询知识图谱确认 "CEO" 具体指代谁（例如 "Alice Smith"），以及她是否确实是该公司的创始人。
# 如果知识图谱中存在三元组 (Alice_Smith, founder_of, Company_X)，则推理得到验证。