自底向上了解CPU的运算
文章目录
-
- 引言
- CPU如何实现逻辑运算
-
- NMOS和PMOS
- 基于MOS管组合下的逻辑门运算
- 逻辑运算下运算的实现
- ALU的诞生
- CPU的诞生
- 关于二进制运算的研究
-
- 十进制转二进制基础换算
- 为什么负数要使用补码进行表示
- 为什么反码就能解决正负数相加问题,我们还需要用补码来表示负数呢?
- 小数的二进制转换
- 计算机如何保存带有小数的数据
-
- 科学计数法
- 如何用二进制空间表示科学计数法的结果
- 详解0.1+0.2==0.3返回false
-
- 问题描述
- 解决方案
- 编程中运算的一点建议
- 小结
- 参考
引言
本文将从CPU演变的视角逐步推进说明CPU演进过程,同时也会针对计算机数学运算过程中一些常见的错误细节进行探讨。
CPU如何实现逻辑运算
NMOS和PMOS
CPU是由晶体管构成,在逻辑上我们一般会将其通过电路符号进行抽象,即分为如下三个连接端:
- 栅级(gate)
- 源极(source)
- 漏极(drain)
基于NMOS而言,从语义上来理解,它是消极的MOS管(N即negative),所以它的电流是逆流而上的,这也就是为什么下图中寄生二极管(即右边的箭头)的朝向是由源极(S)到漏极(D)即通过这样的导向避免漏极电流无条件从漏极流向源极,从N的语义上理解,因为电流是消极的流向,所以输出电流也必须付出更大的努力才能导通电源,所以NMOS的规范为:
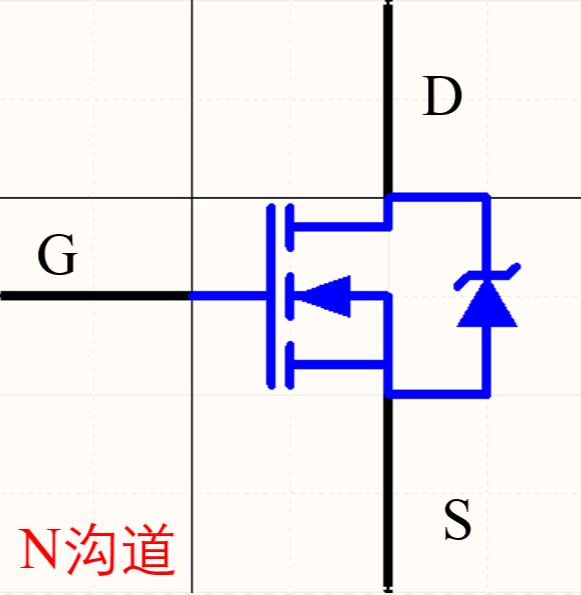
- 当输入二进制1时,栅极闭合,电路导通,电流从漏极流向源极
- 当输入二进制00时,栅极电源断开,电路无法导通
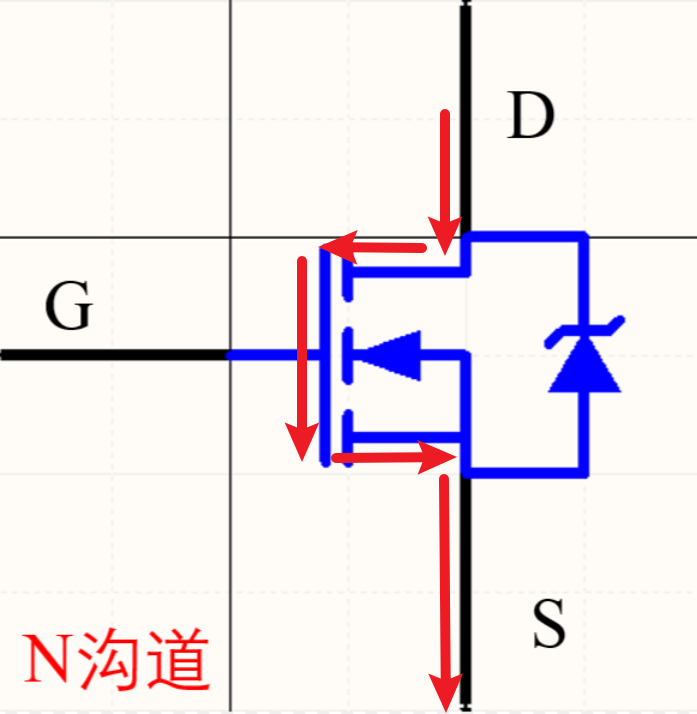
PMOS反之,可以看到寄生二极管从漏极指向源极避免源极无条件流向漏极,因为PMOS是积极的(P即positive),即无需过多努力即可导通电源,所以其电路运行机制为:
- 当输入0时,栅极闭合,电路直接导通,从源极直接流向漏极
- 当输入1,栅极断开,电路无法导通
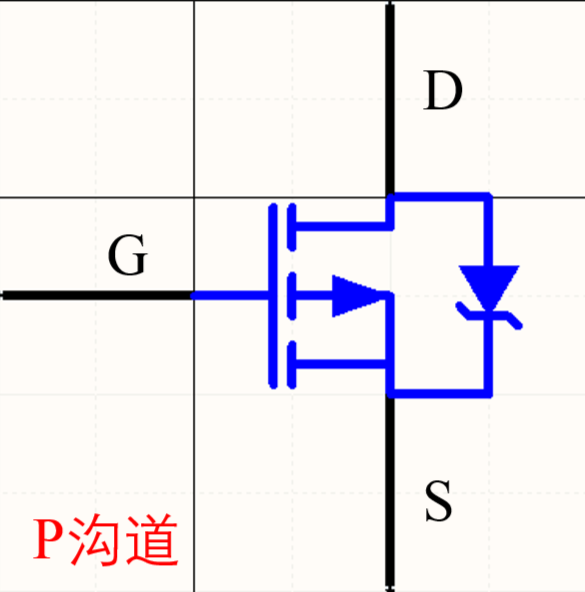
基于MOS管组合下的逻辑门运算
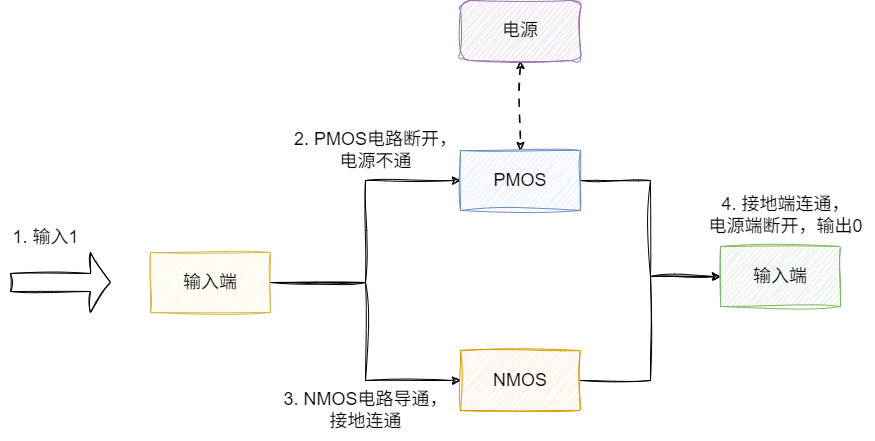
基于上述电路符号的基础上,我们将二者结合,NMOS接地、PMOS接电源,试想这样我们输入数字1:
- 对于
NMOS电源导通,输出端Y导通,接地连同 - 对于PMOS电源断开,与电源端断开
- 最终没有亮起输出0
同理,我们不妨再尝试输入0:
- 对于NMOS电源断开
- 对于PMOS电源导通
- 电源端导通,输出1
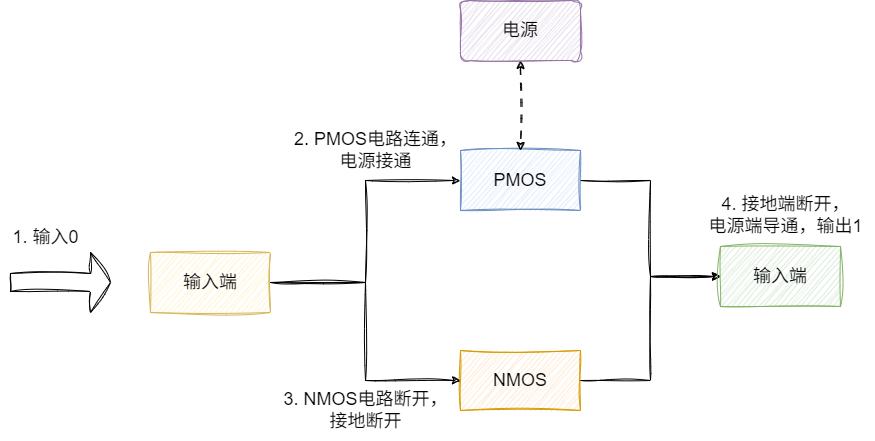
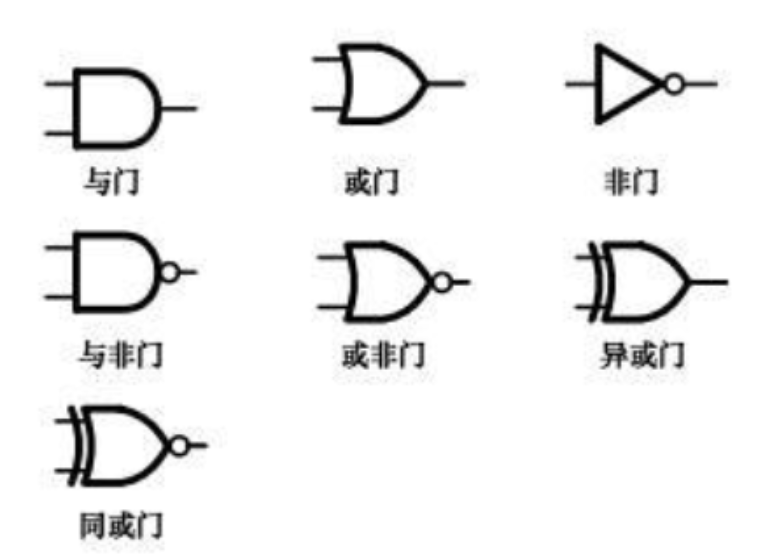
由此可知,输出结果与输入结果相反,就生成二进制中的非运算,而上述的组合我们也称之为非门。同理,设计者们基于NMOS和PMOS这两种晶体管搭建出各种各样的门电路:
- 与门
- 或门
- 非门
- 与非门
- 或非门
- 异或门
- …
逻辑运算下运算的实现
基于逻辑门的基础,我们开始推进计算机运算的步骤,我们都知道计算机是二进制语言,对应我们以加法为例,对应的运算为:
0+0=0即二进制的00+00,最终输出二进制结果为000+1=1即二进制中的00+01,最终输出二进制结果为011+1=2即二进制中的01+01,最终输出二进制结果为10
最终我们将这些数字的二进制运算转为换下图所示的表格,我们以1+1为例,可以看到输出二进制结果为10,对应的低位为0,而进位为1,由此得出10。
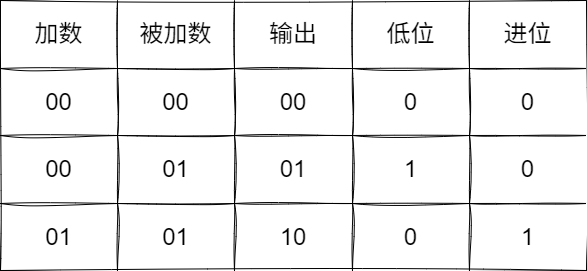
我们从最基础的规律抓起,可以看到低位的0本质上不就是异或运算:
- 第一行低位的0本质上就是
0^0,对应输出0 - 第一行低位的0本质上就是
0^1,对应输出1 - 第一行低位的0本质上就是
1^1,对应输出0
然后我们就需要考虑另一个问题,即进位问题,经过推理发现本质上就是按位与,同样结合表格可以看出,对应的进位本质上就是低位运算的按位与:
- 第一行低位的0本质上就是
0&0,对应输出0 - 第一行低位的0本质上就是
0&1,对应输出0 - 第一行低位的0本质上就是
1&1,对应输出1
最终我们完成低位的加法运算推导过程,即通过:
- 异或门计算低位和
- 与门计算进位
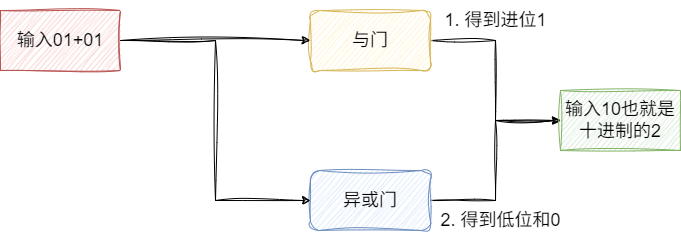
对应的我们将上述的逻辑视图换成如下符号表示,读者可结合图片中的语义自行理解:

但是我们加法中还是涉及一些高位累加的,例如15+9对应9+5的进位就需要参与到高位的运算中,所以说我们目前的加法器只是一个简单的半加法器。
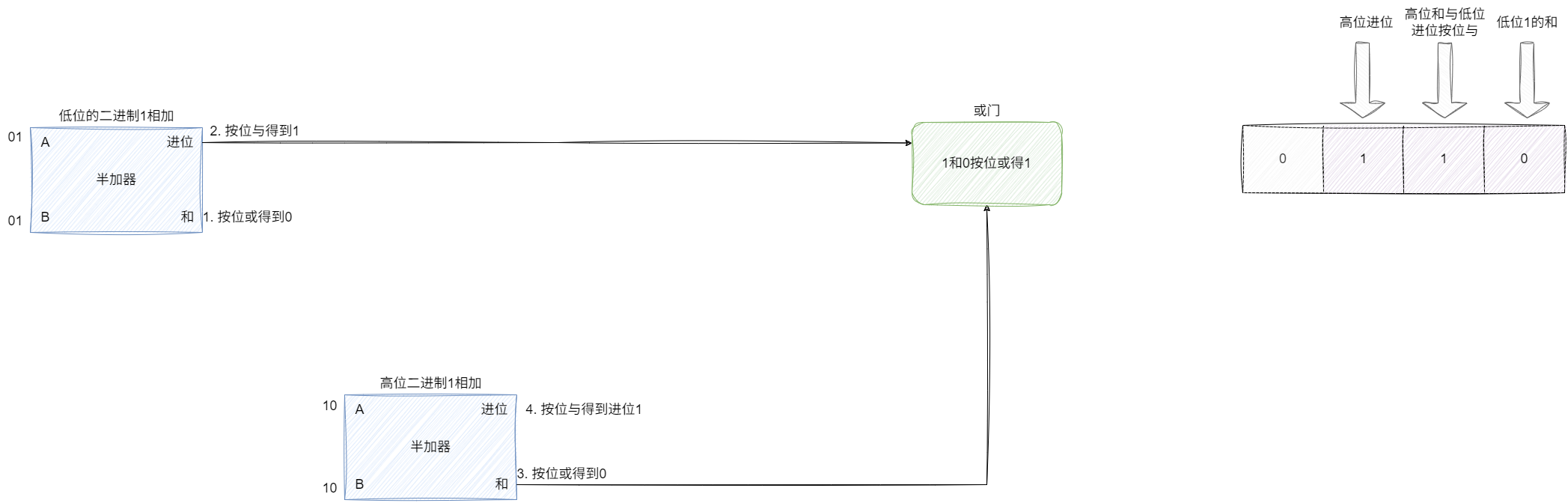
关于二进制进位的运算,通过低位进位和高位和进行按位或解决,我们试想3+3j即二进制的11和11相加,对应的换算步骤为:
- 低位两个1使用半加器算得和为0、进位1。
- 高位两个1使用半加器算得和为0、进位1。
- 因为低位有个进位1,也就是10对应高位的和,两者进行按位或得到1。
- 结合低位和0,高位和和低位进位按位或得到1,高位进位1,得到二进制110也就是6:
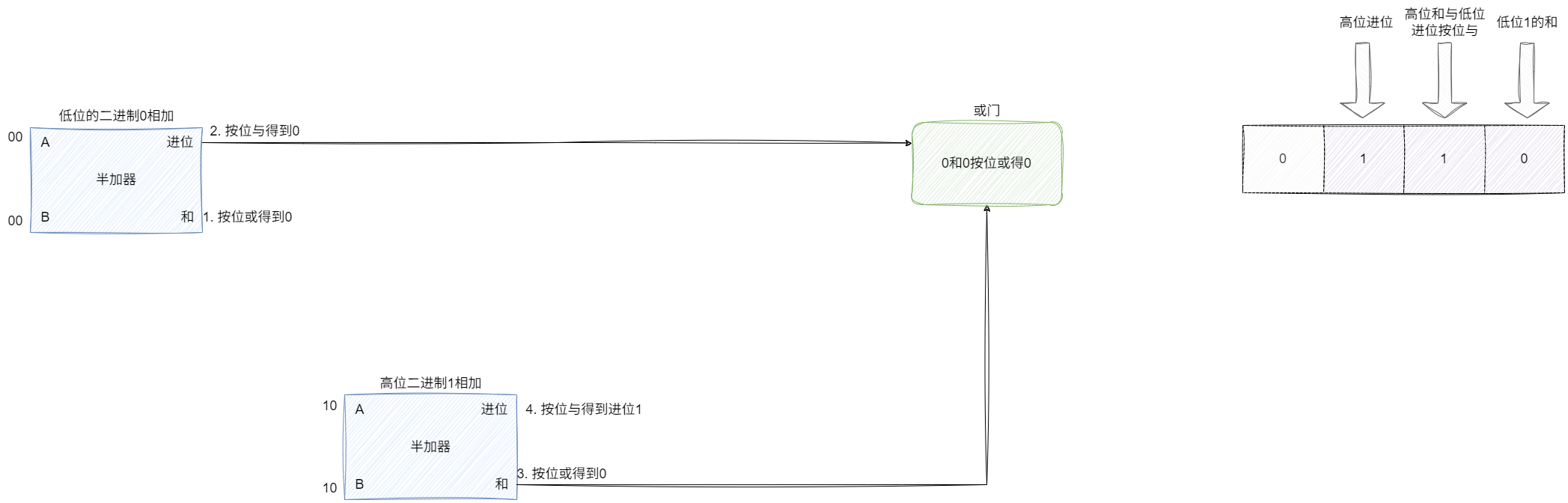
同理我们再演示一下2+2也就是二进制10和10相加:
- 低位算得和0进位也为0
- 高位算得和为0进位为1
- 低位进位0和高位和0按位或得0
- 结合低位0、高位和与低位进位0算法低2位为0,高位进位为1即100
- 最终结果为4
通过这种运算,我们推理出全加法器,在此基础上,串联无数个全加法器生成更高进位的加法运算。
