动态多目标进化算法:VARE(Vector Autoregressive Evolution)求解DF1-DF14,提供完整MATLAB代码
一、VARE简介
VARE(Vector Autoregressive Evolution)算法是2023年提出的一种新型的动态多目标优化(DMO)算法,旨在有效处理随时间变化的多目标优化问题。它通过结合向量自回归(VAR)模型和环境感知超变异(EAH)策略,动态适应环境变化,预测新的 Pareto 最优解,并保持种群多样性。VARE 的主要贡献在于提出了一个能够考虑决策变量之间相互关系的 VAR 模型用于种群预测,并引入 EAH 策略来动态调整种群多样性。
(1)向量自回归(VAR)模型
VAR 模型是一种用于预测相互联系的时间序列系统的统计模型。在 VARE 算法中,VAR 模型用于预测新环境中的解,考虑了决策变量之间的相互关系。VAR 模型的数学形式如下:
x t = α + β 1 x t − 1 + β 2 x t − 2 + ⋯ + β l x t − l + µ x_t = α + β_1x_{t-1} + β_2x_{t-2} + \cdots + β_lx_{t-l} + µ xt=α+β1xt−1+β2xt−2+⋯+βlxt−l+µ
其中:
- x t x_t xt是一个 n 维内生变量向量,表示当前时刻的决策变量。
- α α α 是一个 n 维常数向量。
- β 1 , β 2 , … , β l β_1, β_2, \ldots, β_l β1,β2,…,βl是模型的系数矩阵,表示不同滞后阶数对当前值的影响。
- l l l 是滞后阶数,表示模型考虑的过去时间步数。
- µ µ µ是一个零均值白噪声向量,表示模型的误差项。
在 VARE 中,为了处理高维决策变量带来的参数稀疏问题,使用主成分分析(PCA)进行降维。首先将历史解数据映射到低维空间,然后在低维空间中构建 VAR 模型,最后将预测结果映射回原始决策空间。
(2)环境感知超变异(EAH)策略
EAH 策略用于动态调整种群多样性,以应对环境变化。EAH 根据目标空间和决策空间的变化估计环境变化的严重程度,并据此调整超变异的分布指数。具体计算如下:
客观空间变化度量
在目标空间,EAH 计算所有目标的相对差异平均值 (∆F):
∆ F = 1 M N ∑ i = 1 N ∑ j = 1 M ∣ f j ( x i , t + 1 ) − f j ( x i , t ) f j ( x i , t ) + ε ∣ ∆F = \frac{1}{MN} \sum_{i=1}^N \sum_{j=1}^M \left| \frac{f_j(x_i, t+1) - f_j(x_i, t)}{f_j(x_i, t) + ε} \right| ∆F=MN1i=1∑Nj=1∑M fj(xi,t)+εfj(xi,t+1)−fj(xi,t)
其中:
- M M M 是目标数量。
- N N N是种群大小。
- f j ( x i , t ) f_j(x_i, t) fj(xi,t)是个体 x i x_i xi在时间 t t t的第 j j j个目标值。
- ε ε ε是一个小常数,用于防止除以零。
决策空间变化度量
在决策空间,EAH 计算每个个体的相对决策差异平均值 (∆X):
∆ X = 1 N n ∑ i = 1 N ∑ j = 1 n ∣ x ^ i , j − x i , j x i , j + ε ∣ ∆X = \frac{1}{Nn} \sum_{i=1}^N \sum_{j=1}^n \left| \frac{\hat{x}_{i,j} - x_{i,j}}{x_{i,j} + ε} \right| ∆X=Nn1i=1∑Nj=1∑n xi,j+εx^i,j−xi,j
其中:
- n n n是决策变量的数量。
- x i , j x_{i,j} xi,j是个体 x i x_i xi在时间 t t t 的第 j j j个决策变量值。
- x ^ i , j \hat{x}_{i,j} x^i,j是个体 x i x_i xi 在时间 t + 1 t+1 t+1 的第 j j j 个决策变量值。
分布指数调整
根据 ∆ F ∆F ∆F 和 ∆ X ∆X ∆X计算超变异的分布指数 η η η:
η = 20 × max ( e − ( ∆ F + ∆ X ) , 0.1 ) η = 20 \times \max(e^{-(∆F + ∆X)}, 0.1) η=20×max(e−(∆F+∆X),0.1)
该公式将 η η η 的取值范围限制在 [2, 20],其中 η = 20 η = 20 η=20 表示没有环境变化,而 η ≥ 2 η ≥ 2 η≥2则确保超变异的解不会过于随机。
(3)自适应变化响应机制
VARE 算法通过自适应变化响应机制,在 VAR 预测和 EAH 之间进行选择。选择机制基于过去环境变化中不同策略的成功率。具体来说,为每个参考方向 λ i λ_i λi 定义选择 VAR 预测的概率 π i π_i πi:
π i = ρ i , p ρ i , p + ρ i , m π_i = \frac{ρ_{i,p}}{ρ_{i,p} + ρ_{i,m}} πi=ρi,p+ρi,mρi,p
其中:
- ρ i , s ρ_{i,s} ρi,s是策略 s s s(可以是 VAR 预测或 EAH)在过去 L L L个环境变化中生成的个体被保留下来的比率。
- L L L 是过去环境变化的数量,通常设置为等于 VAR 模型的滞后阶数 l l l。
(4)算法流程
- 初始化:生成均匀分布的参考方向,初始化种群和 VARE 概率向量。
- 环境变化检测:在每一代开始时检测环境是否发生变化。
- 响应环境变化:
- 如果检测到环境变化,将当前种群存档,并根据 VARE 概率决定使用 VAR 预测还是 EAH 生成新个体。
- 若未检测到环境变化,则通过遗传操作生成新种群。
- 多样性中心排序:对当前种群和新生成的个体进行多样性中心排序,更新种群。
- 更新 VARE 概率:根据个体保留的成功率更新 VARE 概率。



(5)关键创新点
- 向量自回归(VAR)模型:用于考虑决策变量之间的相互关系,预测新环境中的解。通过主成分分析(PCA)进行降维,提高模型参数估计效率。
- 环境感知超变异(EAH):根据目标空间和决策空间的变化估计环境变化的严重程度,动态调整超变异的分布指数,增加种群多样性。
- 自适应变化响应机制:根据过去环境变化中不同策略的成功率,自适应选择 VAR 预测或 EAH 作为响应机制。
(6)参考文献
[1] Jiang S , Wang Y , Hu Y ,et al. Vector Autoregressive Evolution for Dynamic Multi-Objective Optimisation[J]. ArXiv, 2023, abs/2305.12752.DOI:10.48550/arXiv.2305.12752.
二、VARE求解DF1-DF14
(1)CEC2018 动态多目标测试函数介绍
CEC2018 竞赛定义了 14 个动态多目标测试函数(DF1-DF14),分为两类:

- 双目标问题(DF1-DF9):这些函数具有两个目标,用于测试算法在动态环境下的性能。
- 三目标问题(DF10-DF14):这些函数具有三个目标,增加了优化的复杂性。
这些测试函数设计了不同的动态特性,以评估动态多目标优化算法的性能。动态特性包括:
- 目标位置变化:Pareto 最优前沿(PF)或 Pareto 最优解集(PS)的位置随时间变化。
- 约束条件变化:动态约束条件的引入或变化。
- 目标数量或决策变量数量变化:在某些测试函数中,目标数量或决策变量数量可能随时间变化。
| 测试函数 | 目标数量 | 动态特性 |
|---|---|---|
| DF1 | 2 | PF 的位置随时间线性移动 |
| DF2 | 2 | PF 的位置随时间非线性移动 |
| DF3 | 2 | PF 的位置和形状随时间变化 |
| DF4 | 2 | PF 的位置和形状随时间剧烈变化 |
| DF5 | 2 | PF 的凸性随时间变化 |
| DF6 | 2 | PF 的凹性随时间变化,并引入局部最优解 |
| DF7 | 2 | PF 的不同部分以不同方向和速度移动 |
| DF8 | 2 | PF 的不同部分以不同方向和速度移动,且存在多个膝点 |
| DF9 | 2 | PF 断裂成多个部分 |
| DF10 | 3 | PF 的位置随时间移动 |
| DF11 | 3 | PF 的位置和形状随时间变化 |
| DF12 | 3 | PF 的位置和形状随时间剧烈变化 |
| DF13 | 3 | PF 的凸性随时间变化 |
| DF14 | 3 | PF 的凹性随时间变化,并引入局部最优解 |
(2)部分MATLAB代码
%% 计算POF
for i=1:size(ArchiveResult{1,1}{1,1},1)/(10*nt*taut)k1=1+(i-1)*(10*nt*taut);k2=k1+nt*taut;if prob_ids<110data=ArchiveResult{1,1}{1,1}(k1:k2,end-1:end);elsedata=ArchiveResult{1,1}{1,1}(k1:k2,end-2:end);endresult(i).data=data;% plot(data(:,1)+i,data(:,2)+i,'ro')% hold on
end
%% 计算TurePOF
prob=problem(prob_ids);
k=1;
for t=0:1:100/taut-1PF(k).data=generatePF(prob,t);PF(k).t=t;k=k+1;
end%% 画图
figure
Fm=size(PF,2);
Tm=size(PF(1).data,2);
if Tm<3for t=1:Fmplot(result(t).data(:,1)+PF(t).t,result(t).data(:,2)+PF(t).t,'ro');hold onplot(PF(t).data(:,1)+PF(t).t,PF(t).data(:,2)+PF(t).t,'g.');endxlabel('f1+t')ylabel('f2+t')
elsefor t=1:Fmplot3(result(t).data(:,1)+PF(t).t,result(t).data(:,2)+PF(t).t,result(t).data(:,3)+PF(t).t,'ro');hold onplot3(PF(t).data(:,1)+PF(t).t,PF(t).data(:,2)+PF(t).t,PF(t).data(:,3)+PF(t).t,'g.');endxlabel('f1+t')ylabel('f2+t')zlabel('f3+t')
end
title(prob.name)(3)部分结果
DF1:

DF4:
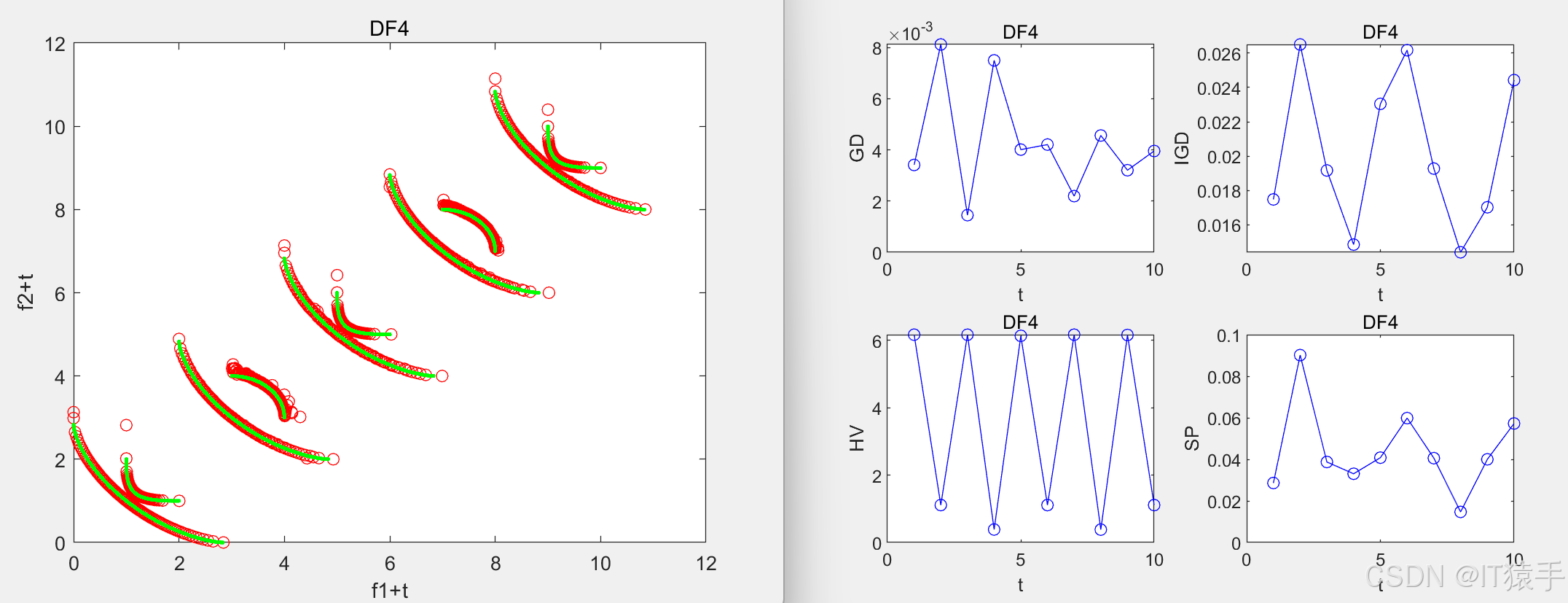
DF10:

