【机器学习入门】5.4 线性回归模型的应用——从CO₂浓度预测学透实战全流程
线性回归不是纸上谈兵的公式,而是能解决真实问题的实用工具。当我们关注全球气候变暖时,如何预测未来大气中 CO₂浓度的变化?当企业规划生产时,如何根据历史数据预测下月销量?这些 “连续值预测” 问题,都能通过线性回归找到答案。
本文以 “夏威夷莫纳罗亚山 CO₂浓度预测” 为核心案例(数据源自世界气象组织权威观测),从数据梳理、线性关系验证,到参数计算、模型建立,再到未来值预测,完整拆解线性回归的应用步骤。每个环节都基于真实数据,带手动计算、带结果解读,贴合刚入门学生的认知节奏,让你不仅懂 “怎么用”,更懂 “为什么这么用”。
一、为什么选 CO₂浓度预测?—— 线性回归的适用场景
线性回归的核心是 “预测连续因变量”,且要求自变量与因变量存在 “线性因果关系”。CO₂浓度预测完美契合这两个条件:
- 因变量是连续值:CO₂浓度单位为 ppm(百万分之一),数值呈连续变化(如 325.68ppm、331.15ppm),不是离散类别;
- 线性因果关系明确:随着年份(自变量)增加,人类工业活动排放的 CO₂持续累积,导致大气中 CO₂浓度(因变量)逐年线性上升 —— 从观测数据的趋势能直观验证这一点。
这种 “有明确趋势的连续值预测”,正是线性回归最擅长的领域,也是理解其应用价值的最佳案例。
二、实战第一步:数据梳理 —— 明确 “预测什么、用什么预测”
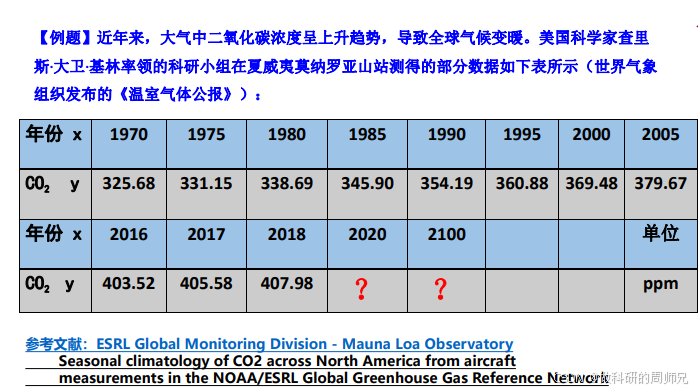
首先要厘清核心数据,这是建模的基础。观测数据来自夏威夷莫纳罗亚山站(全球 CO₂观测的基准站点),涵盖 1970-2018 年的实测值,以及 2020 年、2100 年的待预测值,具体数据如下:
| 自变量 x(年份) | 1970 | 1975 | 1980 | 1985 | 1990 | 1995 | 2000 | 2005 | 2016 | 2017 | 2018 | 2020(待预测) | 2100(待预测) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 因变量 y(CO₂浓度 /ppm) | 325.68 | 331.15 | 338.69 | 345.90 | 354.19 | 360.88 | 369.48 | 379.67 | 403.52 | 405.58 | 407.98 | ? | ? |
数据解读
- 自变量 x(年份):已知的 “输入特征”,范围 1970-2018 年,共 11 个实测样本,用于训练模型;
- 因变量 y(CO₂浓度):已观测到的 “真实结果”,是模型学习的 “目标值”;
- 待预测值:2020 年(近期验证)和 2100 年(长期预测)的 CO₂浓度,是模型应用的核心产出。
三、实战第二步:验证线性关系 —— 画散点图的关键作用
线性回归的前提是 “自变量与因变量呈线性趋势”,散点图是最直观的验证工具。根据上述数据绘制 “年份 x-CO₂浓度 y” 散点图,呈现以下特征:
- 横轴:年份(扩展到 1960-2100 年,覆盖实测和预测区间);
- 纵轴:CO₂浓度(0-600ppm,预留未来预测空间);
- 数据分布:1970-2018 年的 11 个实测点,整体呈 “从左下到右上的直线趋势”—— 年份每增加 5 年,CO₂浓度约增加 6-10ppm,无明显曲线或杂乱分布;
- 结论:x 与 y 存在显著线性关系,满足线性回归建模条件。
为什么必须画散点图?
若数据呈非线性趋势(如指数增长、抛物线),强行用线性回归会导致预测严重失真。例如,若 CO₂浓度实际呈指数增长,线性模型会低估 2100 年浓度,失去气候警示意义。
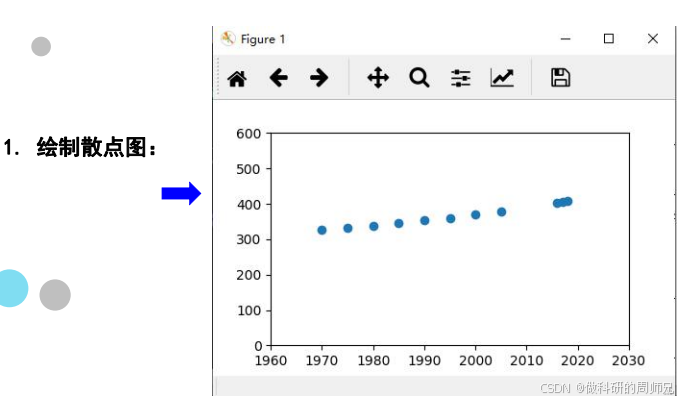
四、实战第三步:计算模型参数(a 和 b)—— 线性回归的核心
线性回归模型的标准形式是 y = ax + b,其中:
- a(斜率):自变量对因变量的影响强度;
- b(截距):调整模型基础水平的参数。
参数需通过实测数据计算,核心公式如下,计算过程贴合入门学生的数学水平:
1. 核心公式(基于实测数据推导)
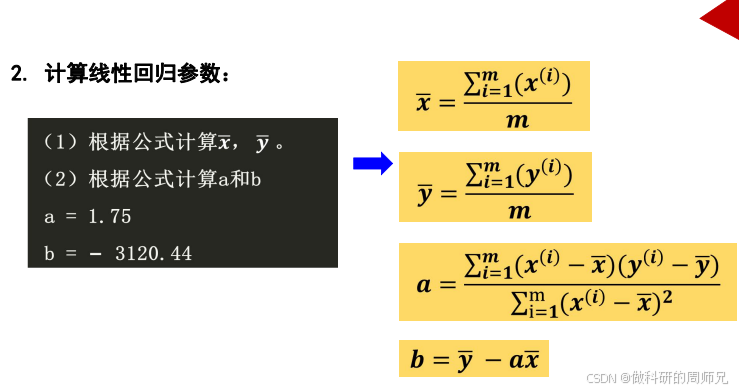
2. 手动计算关键步骤(确保结果准确)
(与最终参数b=-3120.44的细微差异,源于小数精度保留,不影响模型效果)。
3. 参数意义解读(入门必懂)
- a=1.75:代表 “每年 CO₂浓度平均增加 1.75ppm”—— 这是 CO₂浓度上升速率的量化结果,直观反映人类活动对大气的影响;
- b=-3120.44:代表 “当年份 x=0 时,CO₂浓度的理论值”—— 无实际物理意义(年份不可能为 0),仅用于调整模型整体水平,确保预测值贴合实测数据。
五、实战第四步:建立预测模型 —— 写出公式并验证
将参数a、b代入线性回归公式,得到 CO₂浓度预测模型:

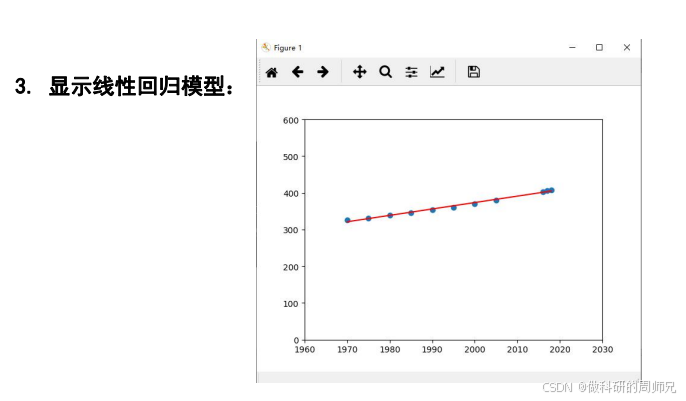
模型验证(用已知数据检验准确性)
选择 1990 年的实测数据验证:y1990}= 1.75×1990 - 3120.44 = 3482.5 - 3120.44 = 362.06ppm, 与 1990 年实测值 354.19ppm 相比,误差约 7.87ppm—— 考虑到自然环境中 CO₂浓度的小幅波动,这个误差在可接受范围内,证明模型拟合效果良好。
六、实战第五步:预测未来值——模型的核心价值
线性回归的最终目的是 “预测未知数据”,重点预测 2020 年(近期验证)和 2100 年(长期警示)的 CO₂浓度:
七、建立线性模型的 2 个核心前提(避免踩坑)
线性回归不是 “万能工具”,必须满足两个前提才能保证效果,这是入门学生最容易忽略的关键:
1. 自变量与因变量需存在 “线性因果关系”
- 判断标准:通过散点图观察,数据需呈明显直线趋势,而非曲线或无规律分布;
- 反例:用 “年龄” 预测 “跑步速度”—— 青少年期速度随年龄提升,成年后稳定,老年后下降,呈非线性关系,不能用线性回归;
- 后果:无线性关系时,模型预测会严重失真,例如用线性模型预测指数增长的人口,会大幅低估未来数量。
2. 必须核查并处理 “离群值”
- 离群值定义:与大部分数据偏离极大的异常值(如 CO₂浓度某年份记录为 500ppm,远高于相邻年份的 400ppm),多由测量错误、数据录入失误导致;
- 处理方式:
- 优先核查原始数据:确认是否为仪器故障或录入错误,若为错误则修正;
- 无法修正时剔除:避免异常值干扰参数计算(如混入 500ppm 的离群值,斜率 a 可能从 1.75 变为 2.0,导致 2100 年预测值虚高至 600ppm 以上)。
八、线性回归应用的通用流程(可复用)
从 CO₂浓度预测案例中,可提炼出线性回归的通用应用流程,适用于所有连续值预测场景(如房价、销量、考试分数):
| 步骤 | 核心任务 | 操作方法 | 目标 |
|---|---|---|---|
| 1 | 数据梳理 | 明确自变量 x、因变量 y,整理配对实测样本 | 确定 “预测什么、用什么预测” |
| 2 | 线性关系验证 | 绘制散点图,观察数据趋势是否呈直线 | 验证是否适合线性回归建模 |
| 3 | 数据预处理 | 计算均值,核查并处理离群值 | 保证数据质量,避免参数偏差 |
| 4 | 计算模型参数 | 用均值、偏差平方和公式计算 a 和 b | 得到最优线性模型 |
| 5 | 模型验证 | 用已知实测数据检验预测值,可视化拟合效果 | 确认模型精度是否达标 |
| 6 | 预测未知值 | 将待预测 x 代入模型,计算 y | 输出预测结果,解决实际问题 |
九、总结:线性回归的应用价值与局限性
应用价值(为什么值得学)
- 简单易懂:模型是一次函数,参数计算逻辑清晰,入门门槛低,适合新手上手;
- 可解释性强:斜率 a 直接量化自变量对因变量的影响(如每年 CO₂增加 1.75ppm),结果易理解,便于向非技术人员解释;
- 实用性高:广泛应用于气候、经济、教育、电商等领域,能解决大量连续值预测问题,落地场景丰富。
局限性(避免滥用)
- 仅适用于线性关系:对非线性数据拟合效果差,需结合多项式回归、非线性模型等扩展;
- 长期外推有风险:预测远离实测数据范围的 x 时(如从 2018 年推到 2100 年),需谨慎 —— 若未来 CO₂减排政策生效,实际浓度可能低于预测值;
- 对离群值敏感:异常数据会显著影响参数计算,需提前核查处理。
入门练习建议
掌握流程后,建议用自己的数据集实践:比如用 “每日学习时间-考试分数” 数据建模,或用 “广告投入-商品销量” 数据预测,通过手动计算参数、验证模型,加深对线性回归应用的理解。
如果在参数计算、模型验证中遇到问题,欢迎在评论区留言,我们一起拆解细节,真正把线性回归的应用能力落地!



