由于不对称GND过孔配置,差分信号过孔上的差模到共模转换
本文研究了靠近高速差分信号过孔的接地过孔的影响以及由此产生的差模到共模的转换。该工作显示了接地 (GND) 过孔和差分信号之间距离的影响 (Diff. SIG.);GND过孔不对称配置的影响;介电厚度和平面之间跃迁次数的影响。
印刷电路板 (PCB) 的密度越来越大、越来越复杂,并且需要满足更高频率的运行要求。为了处理非常高速的数字通信,设计人员通常被迫使用差分信号来实现可接受的信号完整性。然而,这并没有减少控制EMI辐射的需求。当高速差分信号在 PCB 上布线时,目的是使差分对的两个部分尽可能平衡,以确保低 EMC 辐射和对外部和内部噪声的高抗扰度。众所周知,任何少量的成对偏斜、上升/下降时间失配、幅度失配或任何不对称都会在差分信号线上迅速产生大量共模噪声,从而增加EMI辐射[1]。差分信号布线通道的不对称会导致差模到共模转换,从而影响 EMC 辐射和共模到差模转换,从而降低系统对内部和外部噪声源的抗扰度。
这些不对称性延伸到差分信号路径附近的任何不对称性,包括接地参考过孔附近的差分过孔。这项工作研究了差分信号中的模式转换电平作为接地通孔距离、频率、通孔返回对称性、通孔穿过的参考平面数量和介电厚度的函数。差模到共模(DM-to-CM)转换可以通过将差分信号耦合到其他过孔、连接器引脚等上来增加EMI辐射。共模到差模(CM-to-DM)的转换等于DM到CM,并可能导致外部干扰(如ESD)作为差分噪声耦合到差分信号上。
对整个电路板进行全波分析可能非常耗时,而且由于复杂性而通常不可能,因此分析简化的电路板设计可能会有所帮助。简单几何形状的结果可以提供对底层物理原理的理解,并且大多数信号和电源完整性设计工程师可以将其用作整个设计过程中的快速指南。
通过过渡工具在多层中定义模型
用于模拟多氯联苯平面之间效应的腔体共振方法已被证明是快速有效的[1]、[2]。多层过孔过渡工具(MVTT)[2]被用作该分析的主要仿真工具。该工具基于腔体共振方法,将每一层组装在多层PCB中以计算总体结果。它将电源/接地层腔体建模为矩形(定义明确的谐振模式)或无限平面,以避免平面共振,从而限制结果对特定尺寸 PCB 的普遍适用性。在这项研究中,我们使用了无限平面。这使我们能够专注于接地过孔的影响,而不会因电路板尺寸共振而产生混淆。图1为该模型的横截面图。计算S参数的频率范围为0.1GHz至10GHz。使用典型的介电常数为 4.3,金属厚度为 1mil。从MVTT仿真中获得的0.1 GHz至10 GHz之间的传递函数提供了差分信号过孔和走线上DM到CM的幅度。在所有情况下,较低的结果(较高的负数)是可取的。
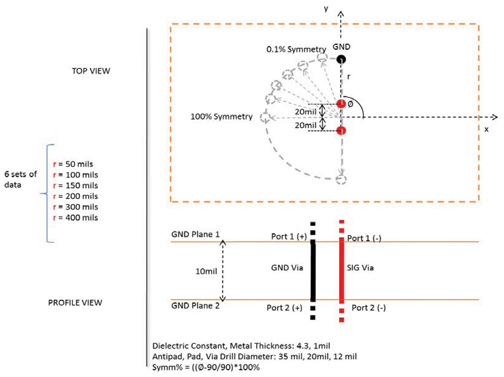
图 1:模型布局(端口 1 和端口 2 是混合模式端口)
模型仿真和结果分析
情况1:在差分SIG附近放置一个GND过孔的情况进行共模转换。 如上所述,我们希望量化由于不对称接地过孔配置而导致的差分信号的模式转换。
产生的共模噪声将存在于平面 [3]、[4]、[5] 之间和 Diff. SIG. 对本身。传递函数是从图 1 所示的模型中获得的,并用作用于数据分析的所有不同模型集的基础。
构成差分信号的信号过孔之间的距离沿 y 轴为 40 密耳。接地过孔 (GND1) 的位置与原点的距离 r 处,其相对于 y 轴的位置因模型而异。随着GND过孔和y轴之间的角度定位增加,我们量化模型对称构型的对称性百分比也会增加。当GND过孔与x轴对齐时,我们说在这种情况下,我们有100%的对称性。
在图 2 中,不同的曲线代表不同的对称配置情况(即 8% 的对称性是最坏的情况,99.7% 的对称性接近完美对称性场景)。正如预期的那样,在较高频率下,所有情况下的模式转换都比在较低频率下多。另一件需要注意的事情是,最好的对称配置也显示出极少的模式转换。
图 2:最佳和最差对称配置情况下的共模转换 (Scd21)
共模噪声作为GND过孔与差分信号
距离的函数图3显示了接地过孔距离和最佳/最坏情况对称性的影响。我们可以观察到,地面通孔的距离会影响对称性(或缺乏对称性)对传递函数的影响程度。
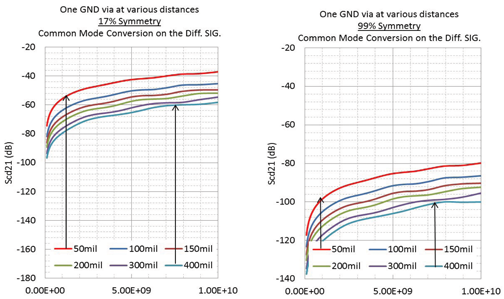
图 3:各种 GND 通孔距离的对称性差和良好的模式转换。
情况 2:在 Diff. SIG 附近放置两个 GND 过孔的情况进行共模转换。
图4中的图表示共模转换的仿真数据,作为频率和对称性的函数[5]。第一个接地过孔 (GND1) 的位置与原点的距离为 r,但始终与 y 轴对齐。虽然第二个接地通孔 (GND2) 也与原点的距离 r 相同,但其相对于 GND1 的位置因型号而异。随着两个GND过孔之间的距离增加,对称性百分比也会增加,我们通过它量化模型的对称配置。当两个GND过孔沿y轴与差分信号对齐时,我们说在这种情况下,我们具有100%的对称性。在考虑GND过孔和差分SIG之间的距离的几个值中,有60mils,如图4所示。当GND过孔接近完美对称配置时,共模噪声会大大降低。当GND过孔与差分SIG中心之间的距离变化时,对称性对共模噪声的影响如图5所示。在图 6 中,我们查看了几个频率点的共模转换作为对称百分比的函数。模式转换量将根据设计要求而有所不同,但在 90% 对称性时,曲线显示出显着的降噪效果。
图 4:不对称性对共模噪声对差分信号的影响
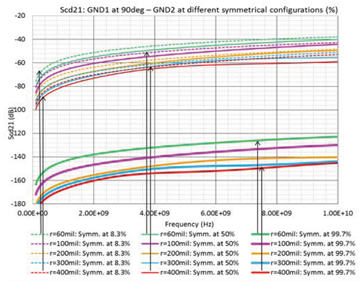
图 5:不对称性对差分信号的共模噪声的影响。比较 GND 过孔的不同对称配置。
图 6:如果对称百分比高于 90%,则差模到共模转换 (Scd21) 会大大降低。
案例 3:模式转换作为两个 GND 过孔情况下 GND 平面数量的函数在本节
中,我们分析了随着过孔穿过的参考平面腔数量增加(对于较厚的 PCB),信号过孔对上的模式转换。在图7中,我们研究了GND过孔相对于Diff.SIG的最佳和最坏情况对称情况。随着平面数量的增加,Scd21 振幅开始收敛。在图 8 中,我们展示了随着参考平面数量的变化,Scd21 的变化如何受到不对称性(最坏情况与最佳情况)的影响。我们选择了几个频率点,并显示了 Scd21 的变化作为平面数量的函数。在高频下,一旦达到收敛,随着GND平面数量的增加,Scd21振幅的变化变化很小。
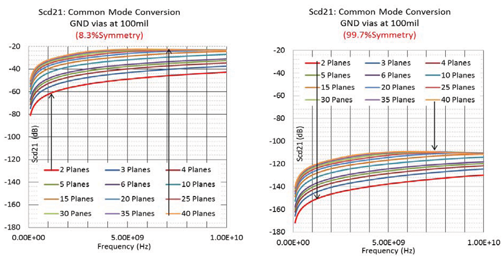
图 7:平面数对共模噪声转换的影响
图 8:共模噪声随差分信号转换的平面数的函数
案例4:对称性对各种介电厚度的Scd21的影响为了
确定介电厚度的影响,分析了许多不同的介电厚度。Scd21 的幅度随电介质厚度而变化,但对于所有不同的介电厚度,最佳和最坏情况对称配置之间的总差异大致相同(图 9)。随着电介质厚度的增加,GND 过孔的影响也随之增加。
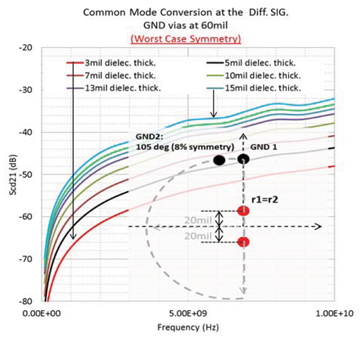
图 9:在对应于不同介电厚度的情况下,Scd21 幅度几乎没有变化。
结论和今后的工作
这项工作量化了从差模到共模的模式转换量,因为GND过孔不对称地放置在差分信号过孔附近。正如预期的那样,当不对称的接地参考过孔接近差分SIG.过孔时,对模式转换的影响最大。这似乎意味着接地参考过孔应远离差分过孔。只有当差分过孔上没有来自其他来源的共模噪声时,这才是正确的。实际上,PCB效应和/或硅不平衡的差分信号上会产生一定量的共模噪声,因此需要靠近差分过孔的接地基准过孔,以允许该共模噪声的返回电流保持接近匹配噪声电流[4]、[5]。因此,由于靠近差分过孔放置的接地参考过孔很重要,并且由于接地参考过孔不对称的影响很大,因此设计规则变成了保持一个或多个靠近差分过孔的接地参考过孔,但要确保它们相对于差分过孔对称放置。设计指南限制可以根据有意差分信号的幅度和传递函数来确定。
模式转换量可不是小事!40 dB 模式转换系数意味着具有 1 V 信号的高速有意信号可能具有 10 mV 的共模噪声幅度。如果这些差分线通过 I/O 连接器连接到非屏蔽电缆,仅此一项就足以导致系统无法通过排放测试。
另一个重要的一点是对称性好和对称性差之间的模式转换量的差异。图2显示了60 dB的增量,而图4显示了多达80 dB的差异。这非常重要,并且很容易在具有高速差分信号的系统中产生通过/失败的差异。
未来的工作将包括其他地面通过配置以及使用遗传算法等工具的优化研究。
引用
- Connor, S.、B. Archambeault 和 M. Mondal。“共模电流对高速差分数据链路中信号完整性和 EMI 的影响。”IEEE EMC 国际研讨会,(2008 年 8 月):1-5。
- de Paulis, F.、Y. Zhang 和 J. Fan。“使用级联 S 参数对多层印刷电路板进行信号/电源完整性分析。”IEEE 电磁兼容性汇刊,第 52 卷,第 4 期,(2010 年 11 月)。
- Gu, X.、R. Rimolo-Donadio、Z. Yu、F. de Paulis、Y. H. Kwark、M. Cocchini、M.B. Ritter、B. Archambeault、A. Ruehli、J. Fan 和 C. Schuster。“用于信号和电源完整性协同分析的基于物理的快速过孔和走线模型。 DesignCon 2010,加利福尼亚州圣克拉拉,(2010 年 2 月)。
- Jaze, A.、B. Archambeault 和
- S.康纳。“由于不同距离的信号过孔与接地过孔导致的平面之间的 EMI 噪声降低”,IEEE 电磁兼容性国际研讨会(2011 年)。
- Jaze, A.、B. Archambeault 和 S. Connor。“由于非对称 GND 过孔配置导致的模式转换。”IEEE 电磁兼容性国际研讨会 (2012)。
- Jaze, A.、B. Archambeault 和 S. Connor。“附近接地过孔对高速单端和差分信号的影响。”设计大会,2013 年。
