AI(1)-神经网络(正向传播与反向传播)
🍋🍋AI学习🍋🍋
🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。
💖如果觉得博主的文章还不错的话,请点赞👍+收藏⭐️+留言📝支持一下博主哦🤞
在神经网络的训练过程中,正向传播和反向传播是两个关键步骤。在这两个阶段中,激活函数和损失函数扮演着不同的角色,并以特定的方式参与其中。下面我将详细说明这两个阶段中激活函数和损失函数是如何工作的。
一、正向传播(Forward Propagation)
1. 输入层到隐藏层
输入数据:首先,输入数据 X 被传递给网络的第一层。
线性变换:对于每一层 ll,输入通过权重矩阵 W[l] 和偏置向量 b[l]进行线性变换。
应用激活函数:然后对 Z[l] 应用激活函数 g[l],得到该层的激活输出。
注意:这里激活函数输出其实就是每个神经元传递给下一层的输入。
2. 隐藏层到输出层
最后一层:在输出层,通常会使用一个特定的激活函数来适应任务的需求。例如:
- 二分类问题:Sigmoid 激活函数,其输出范围为 (0, 1),适合表示概率。
- 多分类问题:Softmax 激活函数,用于将多个输出值转换为概率分布。
- 回归问题:可能不使用激活函数或使用线性激活函数。
计算预测值:最后一层的输出 A[L] 就是我们模型的预测值 Y^。
3. 损失函数
- 计算损失:根据预测值 Y^ 和真实标签 Y,使用选定的损失函数 L(Y,Y^)L(Y,Y^) 来衡量模型的表现。常见的损失函数包括:
- 均方误差(MSE):适用于回归任务。
- 交叉熵损失:适用于分类任务,特别是与 Sigmoid 或 Softmax 配合使用时。
二、反向传播(Backward Propagation)
1. 从输出层开始
起点梯度:反向传播从计算输出层的梯度开始。具体来说,我们首先需要计算损失函数对输出层激活值的导数 ∂L∂A[L]∂A[L]∂L。这个梯度被称为“起点梯度”,因为它标志着梯度回传过程的起始点。
对于不同的损失函数,起点梯度的形式有所不同:
- 均方误差(MSE)+ 线性输出:
- 交叉熵 + Sigmoid/Softmax
2. 计算激活函数的导数
激活函数导数:接下来,我们需要计算激活函数的导数。这取决于使用的激活函数:
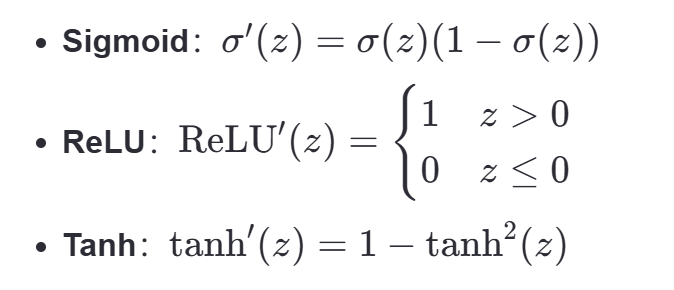
结合起点梯度,我们可以计算出损失相对于线性组合 Z[L] 的梯度
3. 逐层向前传播梯度
正向传播中的作用:
- 激活函数:用于引入非线性,使得网络能够学习复杂的模式。每层的输出都是前一层的激活输出经过线性变换再通过激活函数的结果。
- 损失函数:用于评估模型预测值与真实值之间的差距,提供了一个衡量模型性能的标准。
反向传播中的作用:
- 激活函数:其导数决定了梯度如何从当前层传递到前一层。不同激活函数的导数特性影响了梯度的传播效率和稳定性。
- 损失函数:提供了起点梯度,即损失相对于最后一层激活值的导数。这个初始梯度随后通过链式法则逐层向前传播,用于更新各层的参数。
三、总结:
在正向传播过程中:
1.首先从输入层到隐藏层经过线性变换得到输出值Z,再将输出值经过应用激活函数得到该层的的激活输出A。
2.隐藏层到输出层,在这里通常会使用一个他特定的激活函数来适应任务需求:
二分类问题:Sigmoid 激活函数,其输出范围为 (0, 1),适合表示概率。
多分类问题:Softmax 激活函数,用于将多个输出值转换为概率分布。
回归问题:可能不使用激活函数或使用线性激活函数。
最终计算得到最后一层的输出,也就是我们的预测值。
3.损失函数L:我们开始计算损失根据模型的差异使用不一样的损失函数(最后一层的输出A就是预测值Y)
在反向传播过程中:
1.首先计算损失函数对输出层激活值的导数,这个梯度也就是起点梯度,标志着梯度回传的起始点。
2.计算激活函数的导数A对Z求导,这里取决于使用的激活函数:Sigmoid、ReLU、Tanh等。
结合上起始点的梯度,我们可以计算出损失相对于线性组合 Z[L] 的梯度:
3.逐层向前传播梯度
