Embedding上限在哪里？- On the Theoretical Limitations of Embedding-Based Retrieval

论文：https://arxiv.org/html/2508.21038v1

核心内容总结

该论文由Google DeepMind与约翰·霍普金斯大学团队合作完成，聚焦单向量嵌入模型在信息检索中的根本性局限，通过“理论推导-最优实证-真实任务验证”的三层逻辑，明确维度与文档组合表示能力的核心约束，并提出突破方向，为嵌入模型研究提供关键参考。

一、研究背景与动机

向量嵌入模型近年被广泛应用于检索、推理、指令遵循等任务，研究界常认为“通过更好数据、更大模型可突破现有局限”。但论文指出：此前研究提及的理论局限被归因于“不切实际的查询”，忽视了真实场景中简单查询也可能触发问题；且随着基于指令的检索任务增多（需用逻辑运算符关联文档），模型需表示的top-k文档组合数量激增，单向量范式的固有局限亟待系统性揭示。

二、核心研究内容与关键发现

1. 理论层面：建立“维度-组合表示”的约束关系

• 核心逻辑：单向量嵌入模型通过向量点积建模“查询-文档相关性”，其能返回的top-k文档组合数量，受限于嵌入维度d——维度不足时，必然存在无法覆盖的组合。

• 关键推导：引入“行序保持秩（rankₒₚ）”“行阈值秩（rankᵣₜ）”等定义，关联矩阵符号秩（sign rank）证明：对于二进制相关性矩阵A，模型需至少rank₊(2A-1ₘₓₙ)-1维才能精确表示A的相关性，固定维度d的模型必然存在无法表示的组合。

2. 实证层面：最优场景验证理论（自由嵌入实验）

为排除自然语言、泛化等干扰，验证“局限源于维度本身”，设计无约束向量优化实验：

• 实验设计：向量不依赖预训练模型，直接通过Adam优化器+InfoNCE损失为测试任务定制；数据覆盖所有top-2组合，逐步增加文档数n至模型无法100%准确返回，记录“临界n值”（维度d能覆盖的最大文档数）。

• 结果：维度与临界n值呈三次多项式关系（y=-10.5322+4.0309d+0.0520d²+0.0037d³，R²=0.999）；外推显示512维临界n≈50万、4096维≈2.5亿，远无法满足web-scale检索需求，证明理论约束在理想场景仍成立。

3. 真实任务验证：LIMIT数据集暴露顶尖模型短板

构建极简自然语言数据集LIMIT，聚焦“组合表示能力”：

• 数据集设计：以“人物-喜好属性”为载体（如“Jon likes Quokkas”），查询仅问“谁喜欢X”（k=2），含5万文档（46个核心相关文档+49950个不相关文档）+1000个查询（覆盖46个文档的所有top-2组合），qrel矩阵为“密集模式”（最大化组合数）。

• 测试结果：顶尖单向量模型（GritLM、Gemini Embeddings等）表现极差，完整版本recall@100＜20%，小型版本（46个文档）recall@20不达标；维度越大性能越好，多样化指令训练的模型（如Promptriever）因维度利用更充分表现更优；非单向量模型（BM25稀疏模型、gte-ModernColBERT多向量模型）优势显著，证明突破单向量范式可缓解局限。

• 额外验证：通过“训练集/测试集微调对比”排除“领域偏移”，证实失败源于“组合表示难度”；通过四种qrel模式对比，确认“密集组合”是核心难题。

4. 替代方案探索

指出单向量模型的局限无法通过增大维度规避，提出三类潜在架构：

• 交叉编码器（如Gemini-2.5-Pro）：无维度限制，LIMIT上100%解决任务，但计算成本高，仅适用于重排序；

• 多向量模型（如gte-ModernColBERT）：通过多向量+MaxSim运算提升表达能力，但未适配指令/推理任务；

• 稀疏模型（如BM25）：高维度覆盖更多组合，但依赖词汇重叠，无法应对无词汇关联的指令任务。

三、研究结论与局限性

1. 核心结论

• 单向量嵌入模型的“维度-组合表示能力”约束是根本性局限，仅靠增大维度无法覆盖所有top-k组合；

• 现有评估数据集（如BEIR）因查询覆盖窄无法暴露该局限，LIMIT填补空白；

• 基于指令的检索会加剧组合需求，研究界需跳出“单向量+大维度”思路，探索替代架构。

2. 局限性

• 理论仅适用于单向量模型，未扩展到多向量等架构；

• 未针对“允许部分误差”的场景提供理论约束；

• 无法预先证明模型会在哪些特定组合上失败，仅知存在无法完成的任务。

四、研究价值

首次从理论、实证、真实任务层面系统揭示单向量嵌入模型的根本性局限，打破“更大模型/更多数据可解决所有检索问题”的认知，为检索模型研究指明新方向——聚焦“突破单向量范式”，探索更灵活的表示架构以应对复杂指令检索需求。

1 当前问题

一、核心背景：信息检索的技术演进与任务拓展

1. 技术范式的两次关键转变

过去20年，信息检索（IR）领域完成了从“稀疏技术主导”到“神经模型核心”的跨越：

• 传统阶段：依赖BM25等稀疏技术，通过关键词匹配构建稀疏向量（仅部分维度有值）判断查询与文档相关性，核心是“字面匹配”，泛化能力弱；

• 当前阶段：以神经语言模型（如BERT衍生模型）为基础，采用“单向量嵌入”模式——将查询/文档映射为固定维度的稠密向量（所有维度均有值），通过向量相似度（如余弦相似度）评估相关性，即“稠密检索”。这种模式的核心优势是**泛化性强**，能适配新的检索场景，无需针对特定任务重新设计规则。

2. 模型任务的不断升级与社区期望

随着技术发展，稠密检索模型被赋予越来越复杂的任务：从基础文本匹配，逐步拓展到逻辑组合查询（如“飞蛾或昆虫或瓜德罗普岛的节肢动物”）、推理型检索（如“找和某LeetCode题共享‘动态规划’子任务的题目”）。

为推动技术边界，学术界提出“指令跟随型检索基准”（如QUEST、BRIGHT），要求模型能理解**任意查询的相关性定义**——比如用户自定义“相关”是“包含某子任务”“符合某逻辑规则”，隐含期望是“模型能处理所有可定义的检索任务”，仿佛只要持续优化模型、增加数据，就能突破所有检索难题。

二、研究动机：打破“模型万能”的认知误区

现有研究存在一个关键盲区：多数工作聚焦于“如何通过更大模型、更多训练数据提升嵌入模型性能”，且默认“模型表现差仅因查询不切实际，合理查询总能通过优化解决”。

但本文指出：嵌入模型本质是将文本映射到**几何空间的向量**，其表示能力受限于数学规律（如向量维度、几何空间能承载的“相关性组合数量”）。因此，需跳出“纯实证优化”的思路，从**理论层面**揭示嵌入模型的根本局限性——这正是当前研究的空白。

三、核心研究目标与三大关键方法

本文的核心是“用理论+实证+现实案例，证明嵌入模型存在不可突破的表示局限”，具体通过三方面实现：

1. 理论层面：绑定嵌入维度与表示能力

研究团队借鉴**通信复杂度理论**和**几何代数**，建立了“嵌入维度(d)”与“可表示的top-k文档组合数量”的数学约束关系：

• 核心结论：对于固定的嵌入维度(d)，无论设计何种查询向量，都存在某些“top-k文档组合”（即查询应返回的前k个相关文档），无法通过嵌入模型准确返回。

• 逻辑本质：向量的表示能力由“能编码的‘查询-相关文档’组合数量”决定，而这个数量受限于向量维度——维度越小，能覆盖的组合越少，必然存在“无法表示的组合”，这是数学层面的硬约束，而非“模型没训练好”的问题。

2. 实证层面：验证理论的“理想场景”

为排除“数据不足”“模型结构差”等干扰，研究设计了“自由嵌入优化”实验——模拟“完美嵌入模型”：

• 实验逻辑：不限制向量的自然语言含义，直接用测试集的“查询-文档相关性”标签，通过梯度下降优化向量（相当于让向量“为测试任务量身定制”）；

• 关键发现：每个嵌入维度(d)都有一个“临界点”——当文档数量超过该点，(d)维向量无法编码所有top-k组合；且“维度-临界点”的关系可通过三次多项式精准建模（如(d=512)时，临界点约为50万文档，(d=4096)时约为2.5亿文档）。

• 重要启示：即便在“向量可自由优化”的理想场景，嵌入模型仍受维度限制，现实中受自然语言语义约束的模型，表现只会更弱。

3. 现实层面：用LIMIT数据集直观“显形”局限

为让理论局限更易理解，研究构建了**LIMIT数据集**，用“极简任务难倒SOTA模型”的反差，凸显问题：

• 数据集设计：文档是“人物-喜好”（如“Jon喜欢苹果”），查询是“谁喜欢X？”，仅需返回2个相关文档；但覆盖了“所有可能的top-2组合”（选46个核心文档，其top-2组合共1035个，匹配1000个查询），并加入4.995万不相关文档模拟真实检索干扰；

• 测试结果：即便任务简单，当前最先进的嵌入模型（如Gemini Embeddings、GritLM）在LIMIT上的召回率（Recall@100）仍低于20%，小维度模型更是完全无法完成任务——证明理论局限在现实场景中真实存在。

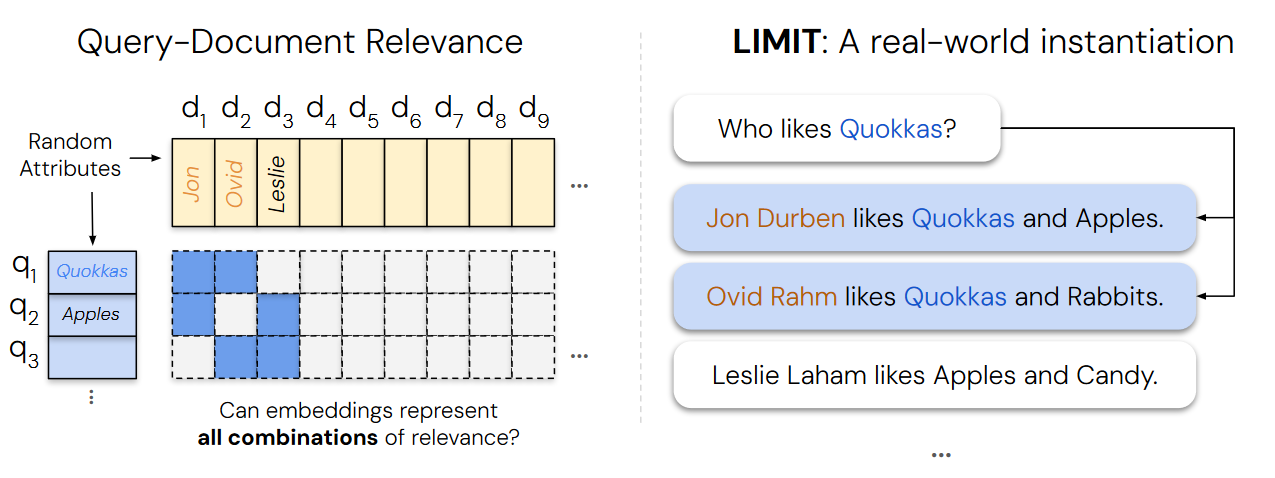
这张图通过左右两部分，直观展现了**“嵌入模型能否表示查询与文档相关性的所有组合”**这一核心问题，并以LIMIT数据集为例，将抽象的理论问题具象为真实世界的自然语言任务。

左侧：查询 - 文档相关性的抽象表示

• 文档（Documents）：图中展示了多个文档（d_1到d_9等），每个文档关联“人物 + 随机属性”（如d_1对应Jon、d_2对应Ovid、d_3对应Leslie）。

• 查询（Queries）：设计了多个查询（q_1、q_2、q_3等），每个查询聚焦一个属性（如q_1是“Quokkas”、q_2是“Apples”）。

• 相关性矩阵（Relevance Matrix）：用蓝色方块表示“查询 - 文档相关”，白色表示“不相关”。矩阵呈现出不同查询与文档的关联组合，核心疑问是：嵌入模型能否表示所有这样的相关性组合？

右侧：LIMIT数据集的真实场景实例

LIMIT是为测试嵌入模型“组合表示能力”构建的自然语言数据集，这里以具体例子说明：

• 查询：“Who likes Quokkas?”（谁喜欢短尾矮袋鼠？）

• 相关文档：

  • “Jon Durben likes Quokkas and Apples.”（Jon Durben喜欢短尾矮袋鼠和苹果）；

  • “Ovid Rahm likes Quokkas and Rabbits.”（Ovid Rahm喜欢短尾矮袋鼠和兔子）；

• 不相关文档：“Leslie Laham likes Apples and Candy.”（Leslie Laham喜欢苹果和糖果）——因不含“Quokkas”，与查询不相关。

通过这种“极简自然语言任务”，LIMIT将左侧抽象的“查询 - 文档相关性组合”问题，落地为模型可直接处理的真实场景，用于验证：**嵌入模型在这类简单任务中，是否仍存在“无法表示所有相关组合”的局限**。

2 相关研究

2.1 神经嵌入模型

近年神经嵌入模型发展迅速，应用从文本网页搜索拓展到指令跟随、多模态检索，进步依托预训练LM、多模态LM及指令跟随技术的突破，检索领域涌现出多模态（如CoPali）、指令跟随（如Instructor）、预训练LM转化（如GritLM）等代表性模型。本文虽聚焦文本表示，但结论适用于所有模态的单向量嵌入模型，且指出模型会随表示范围扩大触及理论局限，这是现有研究未关注的点。

2.2 稠密检索的实证任务

现有研究通过跨领域适配、多指令理解、推理型检索三类任务推动稠密检索边界，使模型聚焦语义理解，需处理的相关性组合激增。此前研究仅观察到模型实证局限（如小维度假阳性多），但未解释根源；本文则建立嵌入维度与查询相关性矩阵符号秩的理论关联，填补这一空白。

2.3 向量的理论局限

传统“k阶沃罗诺伊图”虽与top-k检索相似，但区域数量难约束，对IR指导有限。本文另辟路径，将top-k检索任务转化为数学约束，推导嵌入维度下界，借鉴通信复杂度理论用矩阵符号秩确定边界，还提出通过“自由嵌入实验”间接确定符号秩下界，为嵌入模型维度需求提供理论依据。

3 用数学语言定义“嵌入模型能做什么”

3.1 形式化定义：把“相关性”转化为可计算的数学概念

要分析嵌入模型的能力，首先需要将“查询-文档相关性”“向量得分排序”等模糊概念，转化为严格的数学定义，核心是以下3组定义：

1. 基础场景与向量映射逻辑

• 场景设定：假设有(m)个查询、(n)个文档，用二进制矩阵(A)（A_{ij}=1)表示文档(j)与查询(i)相关，(A_{ij}=0)则不相关）描述“真实相关性”；

• 向量映射：嵌入模型将查询(i)映射为(d)维向量(u_i)，文档(j)映射为(d)维向量(v_j)，用**点积(u_i^T v_j)** 计算“查询-文档相似度得分”；

• 核心目标：得分需满足“相关文档得分＞不相关文档得分”，即通过向量得分还原矩阵(A)的相关性排序。

2. 行序保持秩（rank_{rop} A)：“正确排序”所需的最小维度

• 定义本质：找到一个秩最小的得分矩阵(B)（B_{ij}=u_i^T v_j)，使得(B)能完全还原(A)每一行的“相关性顺序”——只要(A)中“文档(j)比文档(k)相关”（A_{ij}>A_{ik})，(B)中“文档(j)得分就比文档(k)高”（B_{ij}>B_{ik})；

• 通俗理解：这是嵌入模型的“基本要求”——如果连“相关文档排在前面”都做不到，模型就是无效的。(rank_{rop} A)就是满足这个要求的**最小嵌入维度**。

3. 阈值可分秩（rank_{rt} A)、(rank_{gt} A)：“清晰区分”所需的最小维度

除了“排序”，还可通过“阈值”区分相关与不相关文档，由此衍生两个定义：

• 行阈值可分秩（rank_{rt} A)：为每个查询单独设一个阈值(tau_i)，让所有相关文档得分＞(tau_i)，不相关得分＜(tau_i)，满足这个条件的最小维度；

• 全局阈值可分秩（rank_{gt} A)：用**同一个阈值(tau)** 对所有查询生效，满足“相关得分＞(tau)、不相关得分＜(tau)”的最小维度；

• 关键关系：全局阈值比行阈值更严格（一个阈值适配所有查询），因此(rank_{gt} A)通常大于(rank_{rt} A)。

3.2 理论边界：证明“排序”与“阈值”等价，且受限于符号秩

通过两个命题，将前面的定义与“矩阵符号秩”绑定，推导出嵌入维度的“硬约束”。

1. 命题1：行序保持秩 = 行阈值可分秩（rank_{rop} A = rank_{rt} A)

• 证明逻辑：

  • （必要性）若能通过阈值区分（rank_{rt} A)，则必然能正确排序（rank_{rop} A)——因为相关文档得分都在阈值上，不相关都在阈值下，顺序自然正确；

  • （充分性）若能正确排序（rank_{rop} A)，则必然能找到阈值区分（rank_{rt} A)——将“所有相关文档得分的最小值”与“所有不相关文档得分的最大值”中间设为阈值即可；

• 结论意义：“正确排序”和“阈值区分”是嵌入模型表示能力的**同一本质**，不需要额外维度，两者对维度的要求完全一致。

2. 命题2：维度受限于“符号秩”，存在明确上下界

要理解这个命题，首先需明确“符号秩”的定义：

• 符号秩（rank_{pm} M)：将二进制矩阵(A)转化为±1矩阵(M)（M=2A-1)，相关为1、不相关为-1），能“保持(M)中元素符号”的最小矩阵秩——即找到一个低秩矩阵(B)，让(B)中正数对应(M)的1，负数对应(M)的-1。

命题2的核心结论是：

• 通俗解读：

  • 下界：要实现“正确排序/阈值区分”，嵌入维度至少为“符号秩-1”；

  • 上界：维度最多为“符号秩”时，一定能实现“正确排序/阈值区分”；

  • 关键推论：若矩阵(A)的符号秩远大于嵌入维度(d)，**无论如何优化模型，都无法让嵌入模型正确表示所有相关性**——这是数学层面的硬约束，而非工程问题。

3.3 推论：理论结论如何指导实际研究？

将前面的数学推导转化为对嵌入模型实践的指导，核心是两点：

1. 固定维度下，必然存在“无法表示”的检索任务

• 逻辑：存在“符号秩任意大”的相关性矩阵(A)（比如文档数量极多、相关性组合极复杂的矩阵）；

• 结论：对任何固定维度(d)（如512、4096），总有某些检索任务的(A)符号秩＞(d+1)，此时嵌入模型必然失效——这解释了为何在LIMIT数据集上，即使SOTA模型也表现极差。

2. 可通过“自由嵌入优化”间接测符号秩

• 逻辑：若能通过(d)维自由嵌入（直接优化向量，不考虑自然语言约束）实现“行序保持”，则(A)的符号秩≤(d+1)；

• 意义：为“无法直接计算符号秩”（符号秩计算难度极高）提供了替代方案——通过实验找到“能实现排序的最小(d)”，即可间接确定符号秩的上界，这也是第4章“自由嵌入实验”的理论依据。

4 最优场景下的优化实验

一、实验核心目标：锁定维度局限的本质

针对“真实任务中模型表现差，是维度问题还是工程优化（如自然语言理解、训练不足）问题”的质疑，本实验通过构建“无任何现实约束”的理想场景，剥离自然语言建模、数据泛化等干扰因素，直接测试嵌入模型的**理论性能上限**。若此场景下维度不足仍导致任务失败，则可证明“嵌入模型的局限源于维度本身，而非工程优化缺陷”，为前文“嵌入维度受符号秩约束”的理论结论提供最强实证支撑。

二、实验设计逻辑：如何打造“性能上限场景”

为最大化模型拟合能力，实验从“向量优化、数据构造、训练配置”三方面入手，确保结果能反映维度的真实约束：

1. 向量层面：无约束的“自由嵌入”

• 核心设定：不依赖任何预训练语言模型，每个查询/文档的向量均为独立可优化参数，通过梯度下降直接定制——相当于为测试任务“量身打造最优向量”；

• 关键价值：无需学习自然语言语义，无需泛化到新数据，仅需拟合测试集的“查询-文档相关性”，这是嵌入模型能达到的**性能天花板**（真实模型受限于语言理解，性能必然低于此）。

2. 数据层面：全覆盖的“top-k组合”

• 固定k=2（每个查询需返回2个相关文档），构建“所有可能的top-2组合”作为查询：例如n个文档对应n选2个查询（覆盖所有相关性组合）；

• 设计目的：避免测试“模型能否学习特定语义”，转而聚焦“维度能否覆盖所有相关性组合”。当n增大时，组合数呈指数级增长，维度的约束会更快显现。

3. 训练层面：最大化拟合的配置

• 优化策略：用Adam优化器（平衡速度与效果）、InfoNCE损失（高效区分相关/不相关文档），全数据集批量训练（每次更新用所有查询-文档对），并对向量归一化（与真实嵌入模型一致）；

• 早停机制：当损失1000次迭代无下降时停止训练，避免无效计算，确保结果反映“能否拟合”而非“训练时长不足”。

4. 关键指标：临界n值——维度能力的量化标尺

• 定义：逐步增加文档数量n，直到模型无法实现100%准确率（即无法覆盖所有top-2组合），此时的n即为“临界n值”；

• 意义：临界n值直接对应维度d的表示能力——d越大，临界n值越高，能覆盖的相关性组合数越多。

5. 结果建模：多项式拟合与规模外推

• 现实限制：当n过大时，组合数会爆炸（如5万文档的top-20组合数远超宇宙原子数），实验仅测试小n、d；

• 外推价值：通过三次多项式（y=-10.53+4.03d+0.052d²+0.0037d³，R²=0.999）拟合“d-临界n值”关系，可推算大维度表现（如d=512时临界n≈50万，d=4096时≈2.5亿）。

三、实验核心价值：为理论结论“盖棺定论”

1. 验证理论：维度与表示能力的绑定不可突破

外推结果显示，即便理想优化场景下，d=4096的嵌入维度仅能覆盖2.5亿文档的top-2组合，而web-scale检索（数十亿文档）的组合数远超此上限——证明“维度决定表示能力”的理论结论成立，且该约束无法通过工程优化规避。

2. 反衬现实：真实模型的局限更严峻

自由嵌入是“理想场景”，而真实模型需兼顾自然语言理解、泛化到新数据，其能覆盖的组合数远低于理想值。这也解释了为何在LIMIT数据集上，SOTA模型表现极差——即便理想模型都有维度局限，真实模型更无法突破。

5 评测构建与优化

一、为何要关联真实世界数据集？—— 填补“理论”与“现实”的 gap

自由嵌入实验虽能证明“维度不足会导致表示能力受限”，但存在明显局限性：实验中向量可无约束优化，无需学习自然语言语义、无需泛化到新数据，完全是“为测试任务量身定制”的理想状态。而真实嵌入模型需面对自然语言理解、数据泛化等现实挑战，理论结论能否直接迁移至真实模型，仍需验证。

因此，第五章围绕两个关键问题展开：

• 现有主流检索数据集，能否有效暴露嵌入模型的维度局限？

• 真实的最先进（SOTA）嵌入模型，在专门设计的、贴近真实语言场景的任务中，是否会因维度不足而失败？

二、现有数据集的“致命缺陷”—— 测不出维度局限

现有检索数据集（如QUEST、BrowseComp）因标注成本高、计算开销大，在设计上存在明显短板，导致无法发现嵌入模型的维度问题，具体体现在两方面：

1. 查询覆盖范围极小，组合空间近乎“未触碰”

现有数据集的查询数量远不足以覆盖“查询-文档相关性（qrel）的所有组合”。以QUEST数据集为例：

• 规模：含32.5万文档，每个查询需返回20个相关文档；

• 理论组合数：top-20文档的可能组合数达C(325k,20)=7.1×10⁹¹（远超可观测宇宙原子数10⁸²）；

• 实际查询数：仅3357个，仅能覆盖组合空间的“ infinitesimally small part（极小部分）”。

这意味着，模型在现有数据集上表现优异，可能只是“恰好覆盖了有限的测试样本”，而非真正具备应对所有查询组合的能力——现有数据集根本无法测试出维度局限。

2. 查询设计复杂，掩盖核心问题

现有数据集常使用复杂查询运算符（如QUEST的“OR”、BrowseComp的5+条件+范围运算符），这些设计本身会增加任务难度（如逻辑推理、多条件整合），导致模型性能差时，无法判断是“维度不足”还是“无法处理复杂运算符”。例如，QUEST的“Novels from 1849 or George Sand novels”，模型失败可能是因不会处理“OR”逻辑，而非不能表示文档组合——这种设计偏离了“测试维度表示能力”的核心目标。

三、LIMIT数据集：专为测试“维度局限”而生

为精准验证“嵌入模型能否表示所有top-k组合”，研究者摒弃现有数据集的复杂设计，构建了LIMIT数据集——核心思路是“剥离所有无关干扰，只聚焦组合表示能力”，让任务“看似极简”却能直击维度问题的本质。

1. 数据集构建：极简设计，排除干扰

LIMIT以“人物-喜好属性”为核心构建自然语言内容，确保任务无额外难度，具体设计如下：

• 内容载体：文档记录“人物+喜好”（如“Jon likes Quokkas and Apples”），查询仅问“谁喜欢某一属性”（如“Who likes Apples?”）——无需复杂语义理解，仅需匹配“属性与人物”的对应关系；

• 关键约束：

  • 文档短：每人属性＜50个，避免“长文本处理”干扰；

  • 查询简单：每个查询仅含1个属性，排除“多条件整合”难度；

  • 固定k=2：每个查询对应2个相关文档，聚焦“top-2组合”的表示能力（与前文自由嵌入实验的k=2保持一致，便于理论关联）；

• 规模与版本：

  • 完整版本：5万文档（46个核心相关文档+49950个不相关文档）+1000个查询（覆盖46个核心文档的top-2组合，C(46,2)=1035，略多于1000以保证统计性）；

  • 小型版本：仅保留46个核心相关文档，排除“无关文档干扰”，专注测试模型对核心组合的表示能力。

2. qrel矩阵选择：故意选“最难”的密集模式

研究者推测“qrel矩阵关联性越强（即文档组合越密集），模型表示难度越高”（因需覆盖更多组合）。尽管无法通过理论严格证明“最密集矩阵最难”，但基于直觉和理论推导，LIMIT选择“能覆盖最多组合”的密集qrel矩阵——确保数据集能最大化暴露维度局限。

3. 测试模型：覆盖主流类型，对比差异

为全面验证维度局限，研究者测试了两类模型，以凸显“单向量嵌入模型的短板”：

• 单向量嵌入模型：涵盖SOTA模型（如GritLM、Gemini Embeddings、Qwen 3 Embeddings等），维度范围1024-4096，训练方式包括指令微调、硬负样本优化等；

• 非单向量模型：作为对比，包括稀疏模型（BM25）、多向量模型（gte-ModernColBERT）、token级TF-IDF（理论上能100%解决任务，作为“性能上限”参考）。

同时，为验证“维度大小的影响”，所有模型均测试“完整维度”和“截断维度（通过MRL降至32维）”——确保能清晰观察维度与性能的关联。

四、LIMIT测试结果：SOTA模型“集体翻车”，维度是关键

LIMIT的测试结果远超预期：即便任务极简，单向量嵌入模型仍表现糟糕，且维度、模型类型直接决定性能，具体结果如下：

1. 单向量模型性能极差，任务“看似简单却完不成”

• 完整版本：所有单向量模型的recall@100均低于20%——意味着即便返回100个文档，也难以命中2个相关文档；

• 小型版本（仅46个文档）：即便放宽至recall@20，模型仍无法达标——46个文档中返回20个，仍难以覆盖2个相关文档，充分说明模型无法表示所有top-2组合。

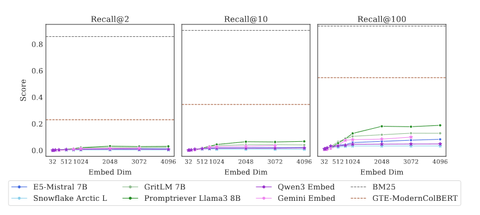
2. 维度越大，性能越好：直接验证理论结论

测试结果显示，嵌入维度与性能呈明显正相关：维度从32维提升至4096维时，模型性能（如recall@2、recall@100）显著上升。例如，GritLM在32维时recall@100接近0，4096维时提升至12.9%——这与前文“维度决定表示能力”的理论结论完全一致，证明真实模型中，维度仍是核心限制因素。

同时，经过多样化指令训练的模型（如Promptriever）表现相对更优，研究者推测其原因是“这类模型能更充分利用嵌入维度”，而仅针对窄范围任务训练的模型（如部分MRL模型），对维度的利用效率较低。

3. 非单向量模型优势显著：突破单向量范式是出路

与单向量模型形成鲜明对比的是，非单向量模型在LIMIT上表现优异：

• BM25（稀疏模型）：得分接近满分，recall@100达93%；

• gte-ModernColBERT（多向量模型）：虽未达满分，但性能远超单向量模型（如recall@100达61.8%）。

这一结果证明，“突破单向量范式”（如稀疏高维度、多向量表示）能有效缓解维度局限——与理论推导中“维度不足是单向量模型的核心问题”相呼应。

五、性能低下的根源：不是“领域偏移”，是“任务固有难度”

面对LIMIT的糟糕结果，研究者首先怀疑“是否因领域偏移（如‘人物-喜好’领域与常见搜索领域不同）导致模型不适应”，为此设计了专门的验证实验：

1. 实验设计：对比“训练集微调”与“测试集微调”

• 模型：选用现成的lightonai/modernbert-embed-large；

• 训练数据：

  • 训练集：用非测试属性合成的“人物-喜好”数据（与LIMIT同领域，排除领域偏移）；

  • 测试集：LIMIT的官方测试集（直接过拟合测试样本）；

• 维度控制：训练时将隐藏层投影到不同维度（32-1024维），而非用MRL。

2. 结果：排除领域偏移，证实“任务固有难度”

• 训练集微调：性能几乎无提升——recall@10从接近0仅升至2.8%，说明模型在同领域数据上训练后，仍无法应对任务，排除“领域偏移”原因；

• 测试集微调：模型可通过过拟合完成任务——仅12维就能拟合46个文档的组合，但64维的真实模型仍无法完全解决，说明真实模型的局限远大于“自由嵌入”（理想场景），核心是“维度不足+自然语言约束”的双重限制。

这一结果进一步证明，LIMIT上模型性能差的根源是“任务固有难度（需表示所有top-k组合）”，而非工程层面的领域适配问题——维度局限是真实且难以通过训练规避的。

六、qrel模式验证：“密集组合”才是真难题

为进一步确认“组合数量决定难度”，研究者用四种不同qrel模式实例化LIMIT（随机、循环、不相交、密集），对比模型性能：

• 非密集模式（随机、循环、不相交）：模型性能相近，且明显优于密集模式；

• 密集模式（LIMIT标准设置）：所有模型性能暴跌——GritLM的recall@100下降50个百分点，E5-Mistral的recall@100从40.4降至4.8（近10倍）。

这一结果直接证实：“需表示的组合越多，模型越难应对”——与前文“维度决定组合表示能力”的理论完全一致，说明LIMIT选择密集qrel矩阵的设计是合理的，且维度局限在组合密集时会被最大化暴露。

七、与MTEB（BEIR）的对比：现有基准“测不准”

MTEB（基于BEIR数据集）是当前主流的嵌入模型评估基准，但研究者发现：模型在BEIR和LIMIT上的性能“无明显相关性”（见图7）。例如：

• Gemini Embeddings在BEIR上得分最高（62.65），但在LIMIT上仅10% recall@100；

• 小型模型（如Snowflake Arctic Embed）在两者上均表现差，主要因维度和预训练知识不足。

这意味着，现有基准（如MTEB）可能让模型“过拟合传统任务”，无法反映模型在“组合表示”上的真实能力——LIMIT的价值在于填补了这一评估空白，能更精准地暴露单向量嵌入模型的维度局限。

八、替代方案：突破“单向量范式”是未来方向

既然单向量嵌入模型的维度局限无法规避，研究者提出三类更具潜力的替代架构，为后续研究提供方向：

1. 交叉编码器（如Gemini-2.5-Pro）

• 优势：无维度限制，通过“一次性处理所有查询和文档”直接建模相关性，在LIMIT小型版本上能100%解决任务（一次前向传播完成1000个查询）；

• 缺点：计算成本极高，无法用于大规模第一阶段检索（如数十亿文档），仅适用于“重排序”（第二阶段）。

2. 多向量模型（如gte-ModernColBERT）

• 优势：通过“多向量+MaxSim运算”提升表达能力，在LIMIT上得分远超单向量模型，且使用的骨干网络（如ModernBERT）规模更小；

• 缺点：尚未适配“基于指令”或“推理类”任务，其表示能力在复杂场景中的迁移性仍需验证。

3. 稀疏模型（如BM25）

• 优势：维度极高（如词汇稀疏向量），能覆盖更多组合，在LIMIT上接近满分；

• 缺点：依赖词汇重叠，无法应对“无词汇/释义重叠”的指令或推理任务（如“找与动态规划相关的Leetcode题”），适用场景有限。

6 结论与局限性

一、核心研究结论

• 理论层面：嵌入维度决定top-k组合表示能力建立理论关联证明，单向量嵌入模型能否表示top-k文档的所有组合，取决于嵌入维度𝑑——仅当𝑑足够大时，模型才能覆盖所有组合；若𝑑不足，则必然存在无法表示的组合，这是模型的固有约束。

• 实证层面：最优场景验证理论有效性通过“自由嵌入实验”（无自然语言约束、向量直接为测试任务优化的理想场景），从实证上验证了上述理论：即便在性能上限场景，维度不足仍会导致模型无法覆盖所有top-k组合，且维度与可表示的组合数量呈明确关联（如三次多项式关系）。

• 现实层面：LIMIT数据集暴露顶尖模型短板将理论转化为简单自然语言任务，构建LIMIT数据集。结果显示，当前最先进（SOTA）的单向量嵌入模型（如GritLM、Gemini Embeddings等）均无法完成该任务，证明理论局限在真实模型中客观存在。同时指出，随着基于指令的检索任务增多（需关联更多文档组合），这种维度局限将愈发明显，研究界需重点关注。

二、研究的局限性

研究虽明确了单向量嵌入模型的核心问题，但仍存在三方面未解决的问题，需后续研究完善：

• 理论不适用于非单向量架构现有理论与实验仅针对“单向量嵌入模型”，无法直接推广到多向量模型等其他架构。尽管团队展示了多向量模型（如gte-ModernColBERT）在LIMIT上的初步优势，但尚未将理论关联扩展到这类模型，其表示能力的约束条件仍不明确。

• 未覆盖“允许误差”的场景研究仅聚焦“需精确表示所有top-k组合”的场景，未针对“用户允许部分误差（如仅需覆盖大部分组合）”的现实情况提供理论结果，也未为这类场景设定维度与误差容忍度的关联约束，相关工作需参考Ben-David等人[2002]的研究进一步探索。

• 无法预先确定“失败组合类型”虽从理论上证明“存在嵌入模型无法表示的组合”，但无法预先判断模型会在哪些特定类型的组合（如特定指令、推理逻辑对应的组合）上失败。这意味着，模型可能在部分基于指令或推理的任务中表现优异，但必然存在其永远无法完成的任务，具体“失败边界”仍需进一步研究界定。