【Luogu】P2398 GCD SUM (容斥原理求gcd为k的数对个数)

P2398 GCD SUM - 洛谷

题目：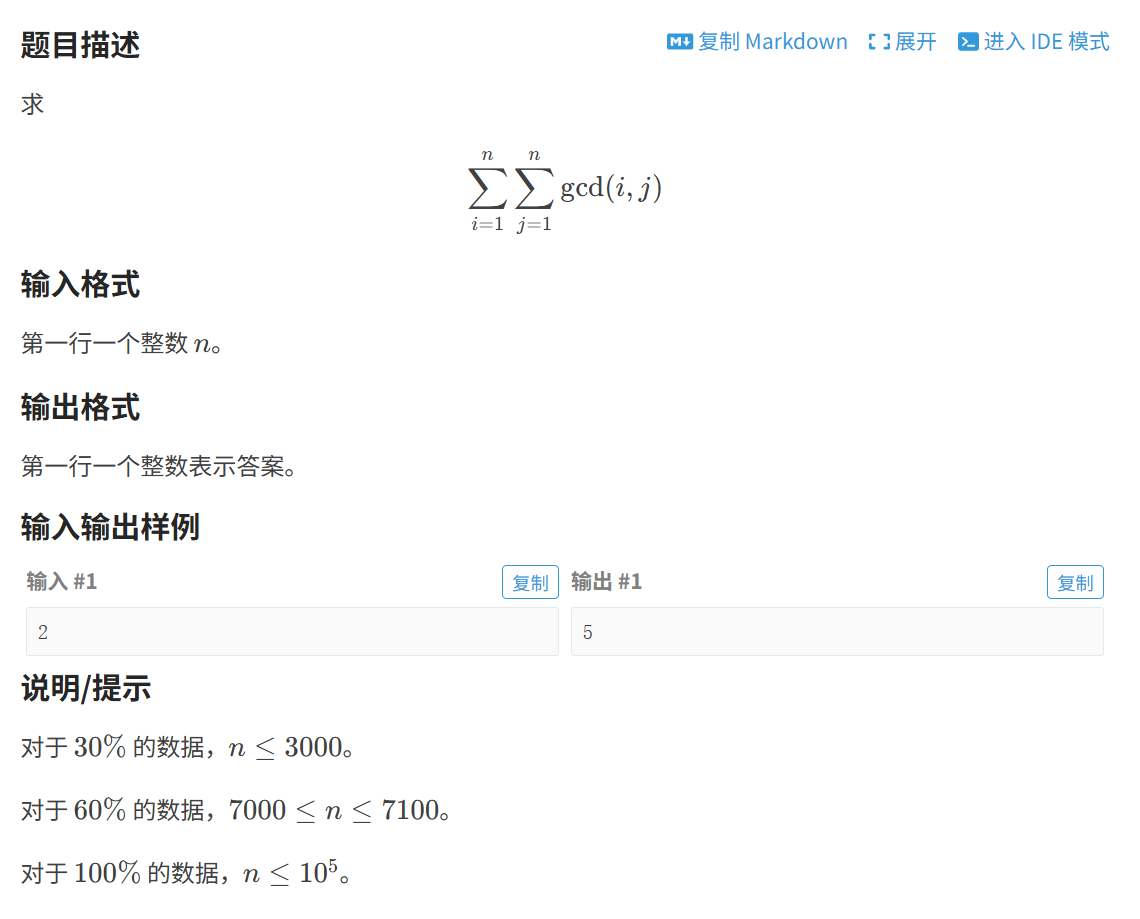

思路：

gcd容斥

令 f[i] 代表以 i 为最大公因数的数对，g[k] 为满足 k | gcd(x,y) 的对数

显然 g[i] = f[i] + f[2*i] + f[3*i] + ... + f[m*i]

不难看出 g[i] = cnt²，其中 cnt 代表 i 的倍数，其值为 n / i

故得 f[i] = cnt² - f[2*i] - f[3*i] - ... - f[m*i]

模拟即可，复杂度约为 O(N·ln(n))

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());int n;
int f[100005];
void solve()
{cin >> n;int ans = 0;for (int i = n; i; i--){int cnt = n / i;for (int j = i; j <= n; j+=i){f[i] -= f[j];}f[i] += cnt * cnt;ans += f[i]*i;}cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;while (t--){solve();}return 0;
}