【LeetCode热题100道笔记】排序链表

题目描述

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例 1：

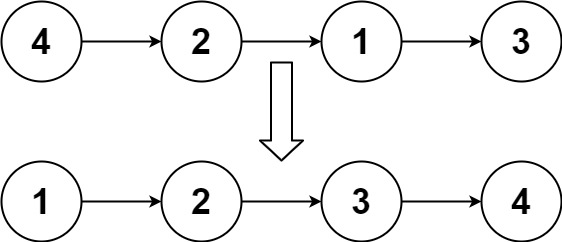
输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

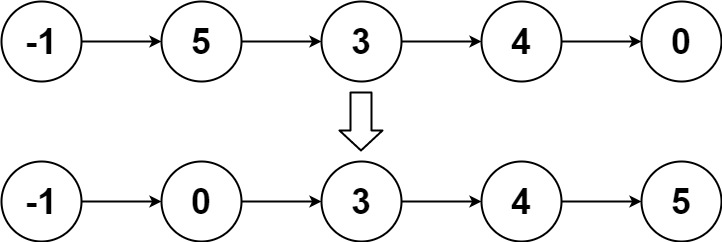
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：
输入：head = []
输出：[]

提示：
链表中节点的数目在范围 [0, 5 * 104] 内
-105 <= Node.val <= 105

进阶：你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

思考一：堆排序

1. 构建最小堆：遍历链表，将所有节点逐个加入最小堆（存储节点本身，需先断开原节点的next指针避免环）。
2. 弹出构建新链表：从堆中依次弹出最小节点，串联成有序链表。

算法过程

1. 初始化：创建一个最小堆（按节点值比较）和遍历指针。
2. 入堆：遍历链表，每个节点断开next指针后加入堆，确保堆中节点独立。
3. 出堆构建：新建哨兵节点，循环弹出堆顶（最小节点）并接入新链表，直至堆空。
4. 返回结果：哨兵节点的next即为排序后链表头。

复杂度

• 时间复杂度：O(n log n)，入堆和出堆各需O(n log n)。
• 空间复杂度：O(n)，堆存储所有节点。

代码

/*** Definition for singly-linked list.* function ListNode(val, next) {*     this.val = (val===undefined ? 0 : val)*     this.next = (next===undefined ? null : next)* }*/
/*** @param {ListNode} head* @return {ListNode}*/
var sortList = function(head) {const minHeap = new MinHeap((a, b) => a.val - b.val);let p = head;while (p) {let tmp = p.next;p.next = null;minHeap.add(p);p = tmp;}const guard = new ListNode();p = guard;while (!minHeap.isEmpty()) {p.next = minHeap.pop();p = p.next;}return guard.next;
};class MinHeap {constructor(compare) {this._data = [];this._compare = compare;}add(num) {this._data.push(num);this.swim();}pop() {if (this._data.length === 0) return;[this._data[0], this._data[this._data.length-1]] = [this._data[this._data.length-1], this._data[0]];const node = this._data.pop();this.sink();return node;}isEmpty() {return this._data.length === 0;}swim(index = this._data.length-1) {while (index > 0) {let pIndex = Math.floor((index-1)/2);if (this._compare(this._data[index], this._data[pIndex]) < 0) {[this._data[index], this._data[pIndex]] = [this._data[pIndex], this._data[index]];index = pIndex;continue;}break;}}sink(index = 0) {const n = this._data.length;while (true) {let left = 2 * index + 1;let right = left + 1;let biggest = index;if (left < n && this._compare(this._data[left], this._data[index]) < 0) {biggest = left;}if (right < n && this._compare(this._data[right], this._data[biggest]) < 0) {biggest = right;}if (biggest !== index) {[this._data[biggest], this._data[index]] = [this._data[index], this._data[biggest]];index = biggest;continue;}break;}}}

思考二：自顶向下归并排序

核心是分治思想：用快慢指针找链表中点，将链表递归拆分为左右两个子链表，直到子链表仅含1个节点（天然有序）；再递归合并两个有序子链表，最终得到完整有序链表。

算法过程

1. 递归终止条件：

   • 若当前链表为空（head === null），直接返回空；
   • 若当前链表仅含1个节点（head.next === tail），断开该节点的next指针（避免后续合并出现环），返回该节点。

2. 拆分（分）：

   • 用快慢指针找中点：慢指针（slow）每次走1步，快指针（fast）每次走2步，当fast到达tail时，slow即为当前链表中点；
   • 递归拆分左子链表（head到mid）和右子链表（mid到tail）。

3. 合并（治）：

   • 调用合并函数，将左右两个有序子链表合并为一个新的有序链表；
   • 返回合并后的链表头，完成当前层级的递归回溯。

关键辅助：合并有序链表

1. 新建哨兵节点（dummyHead），用指针temp遍历并构建合并链表；
2. 双指针分别遍历两个有序子链表，每次将值更小的节点接入temp后；
3. 遍历结束后，将剩余未接入的子链表节点直接接在temp尾部；
4. 返回哨兵节点的next（即合并后的有序链表头）。

复杂度

• 时间复杂度：O(n log n)，拆分需O(log n)层递归，每层合并需O(n)（遍历所有节点）。
• 空间复杂度：O(log n)，递归调用栈深度等于拆分层数（即链表高度），最坏为O(n)（链状链表），平均为O(log n)。

代码

/*** Definition for singly-linked list.* function ListNode(val, next) {*     this.val = (val===undefined ? 0 : val)*     this.next = (next===undefined ? null : next)* }*/
/*** @param {ListNode} head* @return {ListNode}*/
var sortList = function(head) {return toSortList(head, null);
};function toSortList(head, tail) {if (head === null) return head;if (head.next === tail) {head.next = null;return head;}let slow = head, fast = head;while (fast !== tail) {slow = slow.next;fast = fast.next;if (fast !== tail) {fast = fast.next;}}const mid = slow;return merge(toSortList(head, mid), toSortList(mid, tail));
}function merge(head1, head2) {const dummyHead = new ListNode(0);let temp = dummyHead, temp1 = head1, temp2 = head2;while (temp1 !== null && temp2 !== null) {if (temp1.val <= temp2.val) {temp.next = temp1;temp1 = temp1.next;} else {temp.next = temp2;temp2 = temp2.next;}temp = temp.next;}if (temp1 !== null) {temp.next = temp1;} else if (temp2 !== null) {temp.next = temp2;}return dummyHead.next;
}

思考三：自底向上实现归并排序

核心是分治思想的迭代实现：无需递归栈，从最小有序单元（单个节点）开始，按“子链表长度翻倍”的规则，逐层合并相邻子链表，最终得到完整有序链表。该方式避免了递归栈开销，实现常数级空间复杂度，满足题目进阶要求。

算法过程

1. 预处理：

   • 若链表为空，直接返回null；
   • 遍历链表统计总长度length，用于控制合并的终止条件；
   • 新建哨兵节点dummyHead，其next指向原链表头，方便后续统一处理链表连接。

2. 迭代合并（子链表长度递进）：

   • 初始子链表长度subLen = 1（单个节点天然有序），每次循环后subLen <<= 1（左移1位，即长度翻倍），直到subLen >= length（所有节点合并为一个有序链表）；
   • 每次按当前subLen处理链表：
     1. 初始化prev（记录已合并部分的尾节点，初始为dummyHead）和curr（当前待拆分节点，初始为原链表头）；
     2. 拆分相邻子链表：
        • 拆分左子链表head1：从curr开始取subLen个节点，curr最终停在head1的尾节点；
        • 拆分右子链表head2：从curr.next开始取subLen个节点（若剩余节点不足则取全部），并断开head1与head2、head2与后续节点的连接（避免合并时出现环）；
     3. 合并子链表：调用merge函数，将head1和head2合并为有序子链表；
     4. 连接与更新：将合并后的子链表接入prev尾部，更新prev到当前合并子链表的尾节点，再将curr指向未处理的节点，重复步骤2-4直到遍历完链表。

3. 辅助函数：合并两个有序链表：

   • 新建哨兵节点dummyHead，用temp指针遍历并构建合并链表；
   • 双指针temp1、temp2分别遍历head1、head2，每次将值更小的节点接入temp后；
   • 遍历结束后，将剩余未接入的子链表节点直接接在temp尾部；
   • 返回dummyHead.next（即合并后的有序链表头）。

复杂度分析

复杂度	说明
时间复杂度	O(n log n)
	合并轮次：子链表长度从1翻倍到>=n，共需log n轮； 每轮操作：遍历所有节点完成合并，总操作次数为O(n)，故总时间为O(n log n)。
空间复杂度	O(1)
	仅用有限个指针（prev、curr、head1、head2等）和哨兵节点，无额外空间消耗，满足题目“常数级空间”的进阶要求。

核心优势（对比自顶向下归并）

• 空间更优：避免递归栈的O(log n)空间开销，仅用常数空间；
• 稳定性好：归并排序本身是稳定排序，不会改变相同值节点的相对顺序；
• 适配大规模链表：无需递归深度限制，更适合节点数极多（如题目提示的5*10^4）的链表场景。

代码

/*** Definition for singly-linked list.* function ListNode(val, next) {*     this.val = (val===undefined ? 0 : val)*     this.next = (next===undefined ? null : next)* }*/
/*** @param {ListNode} head* @return {ListNode}*/
var sortList = function(head) {if (head === null) return head;let length = 0;let node = head;while (node !== null) {length++;node = node.next;}const dummyHead = new ListNode(0, head);for (let subLen = 1; subLen < length; subLen <<= 1) {let prev = dummyHead, curr = dummyHead.next;while (curr !== null) {let head1 = curr;for (let i = 1; i < subLen && curr.next !== null; i++) {curr = curr.next;}let head2 = curr.next;curr.next = null;curr = head2;for (let i = 1; i < subLen && curr != null && curr.next !== null; i++) {curr = curr.next;}let next = null;if (curr != null) {next = curr.next;curr.next = null;}const merged = merge(head1, head2);prev.next = merged;while (prev.next !== null) {prev = prev.next;}curr = next;}}return dummyHead.next;
};function merge(head1, head2) {const dummyHead = new ListNode(0);let temp = dummyHead, temp1 = head1, temp2 = head2;while (temp1 !== null && temp2 !== null) {if (temp1.val <= temp2.val) {temp.next = temp1;temp1 = temp1.next;} else {temp.next = temp2;temp2 = temp2.next;}temp = temp.next;}if (temp1 !== null) {temp.next = temp1;} else if (temp2 !== null) {temp.next = temp2;}return dummyHead.next;
}