当前位置：首页 > news >正文

力扣hot100:搜索二维矩阵 II(常见误区与高效解法详解)（240）

news 2025/9/6 5:26:07

在 LeetCode 的“搜索二维矩阵 II”问题中，我们需要判断一个目标值 target 是否存在于一个满足以下特性的二维矩阵中：

本文先分析一种常见的错误解法，再介绍一种高效的解决方案。

初始代码的问题分析

这是我第一次写的代码，因为我感觉他有点像二叉树，就尝试了一下，从一个起点出发，尝试在对角线上移动，并检查相邻元素：

class Solution {public boolean searchMatrix(int[][] matrix, int target) {int x = matrix.length - 1;int y = matrix[0].length - 1;int i = 0, j = 0;while (i >= 0 && j >= 0 && i <= x && j <= y) {if (matrix[i][j] < target) {i++;j++;} else if (matrix[i][j] == target) {return true;} else if (matrix[i][j] > target) {int i_temp = i;int j_temp = j;i--;j--;while (i >= 0 && j >= 0 && i <= x && j <= y) {if (matrix[i_temp][j] == target || matrix[i][j_temp] == target) {return true;}i--;j--;}}}return false;}
}

主要问题：

路径不可靠：通过同时增加 i 和 j （如 i++, j++ ）沿对角线移动，但矩阵的特性不能保证对角线上的连续性，容易跳过目标值。
边界处理不当：当索引超出矩阵边界时，逻辑复杂且易出错（如移动到 (3,3) 在 3×4 矩阵中导致越界）。
效率低下：最坏情况时间复杂度为 O(n2)O(n2)（如目标值在左上角时）。

在提交时出现了这种抽象用例导致了错误

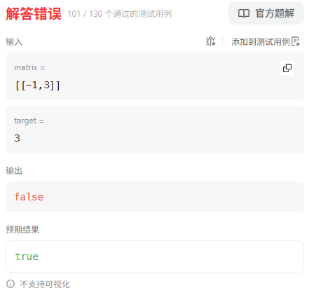
高效解法：从右上角开始搜索

利用矩阵的升序特性，可从右上角（或左下角）开始搜索：

若当前元素等于目标值，返回 true
若当前元素大于目标值，向左移动一列（排除当前列）
若当前元素小于目标值，向下移动一行（排除当前行）

步骤图解：

示例矩阵：
[[1, 4, 7, 11],[2, 5, 8, 12],[3, 6, 9, 16],[10,13,14,17]
]
目标值：51. 从右上角11开始：11 > 5 → 左移至7
2. 7 > 5 → 左移至4
3. 4 < 5 → 下移至5
4. 5 == 5 → 找到目标！

代码实现：

class Solution {public boolean searchMatrix(int[][] matrix, int target) {if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {return false;}int row = 0;int col = matrix[0].length - 1; // 从右上角开始while (row < matrix.length && col >= 0) {int current = matrix[row][col];if (current == target) {return true;} else if (current > target) {col--; // 向左移动} else {row++; // 向下移动}}return false;}
}

复杂度分析：