【LeetCode热题100道笔记】旋转图像

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

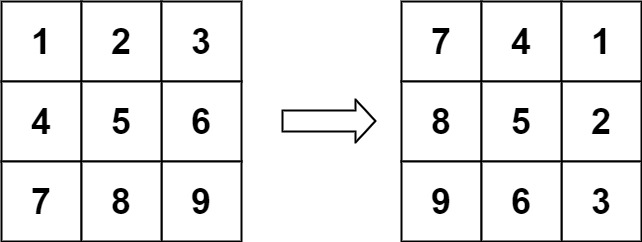
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

思考一（转置翻转）

先转置矩阵，再交换矩阵列

代码

/*** @param {number[][]} matrix* @return {void} Do not return anything, modify matrix in-place instead.*/
var rotate = function(matrix) {const n = matrix.length;for (let i = 0; i < n; i++) {for (let j = 0; j < n; j++) {if (i <= j) {[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];}}}for (let i = 0; i < n; i++) {for (let j = 0; j < Math.floor(n/2); j++) {[matrix[i][j], matrix[i][n-j-1]] = [matrix[i][n-j-1], matrix[i][j]];}    }
};

思考二

分层旋转（从外到内逐层处理），核心是通过 “临时变量” 循环交换每一层的 4 个对应元素，同样能实现原地旋转。
将n×n矩阵看作“嵌套的正方形环”，从最外层（第0层）到最内层（第k层，k = Math.floor(n/2)），逐层处理每个环的元素：

• 对于第 layer 层（从0开始），该层的“边长”为 len = n - 2*layer，需要处理 len-1 组元素（每组4个元素对应旋转后的位置）。

• 每组元素的坐标规律（以第 layer 层为例）：

  • 左上角元素：(layer, layer + offset) → 旋转后到右上角；
  • 右上角元素：(layer + offset, n-1 - layer) → 旋转后到右下角；
  • 右下角元素：(n-1 - layer, n-1 - layer - offset) → 旋转后到左下角；
  • 左下角元素：(n-1 - layer - offset, layer) → 旋转后到左上角；
  • （offset 为每组的偏移量，从0到 len-2）。

• 时间复杂度$O(n^2)$

代码

const n = matrix.length;// 从外到内逐层处理，共 Math.floor(n/2) 层for (let layer = 0; layer < Math.floor(n / 2); layer++) {const len = n - 2 * layer; // 当前层的边长const last = n - 1 - layer; // 当前层的最后一个索引（行/列相同）// 处理当前层的每一组4个元素（共 len-1 组）for (let offset = 0; offset < len - 1; offset++) {// 1. 保存左上角元素（临时变量）const temp = matrix[layer][layer + offset];// 2. 左下角 → 左上角matrix[layer][layer + offset] = matrix[last - offset][layer];// 3. 右下角 → 左下角matrix[last - offset][layer] = matrix[last][last - offset];// 4. 右上角 → 右下角matrix[last][last - offset] = matrix[layer + offset][last];// 5. 左上角（临时）→ 右上角matrix[layer + offset][last] = temp;}}