电机控制(二)-控制理论基础

控制方法

什么是控制？控制系统环路的三要素：基准，反馈，输出

关于控制：控制理论存在于任何工科甚至商科，控制的应用由来已久，但是控制理论起源于1940年，框图，传递函数等传统控制理论。从1960年开始，随着太空探索、电子控制器以及非线性系统的越来越多，控制的研究范式从传递函数转向了状态空间，也就是现代控制理论，随之衍生出了最优控制，非线性控制，卡尔曼滤波等。1980年随着对稳定性的要求越来越高，开始进行鲁棒控制研究。2000年随着单片机和个人电脑的普及，低成本控制。2020年随着算力成本不断降低以及人形机器人热，强化学习开始大放光彩。

现代控制vs经典控制

控制根据研究方法可以分为经典控制理论和现代控制理论。
经典控制理论中，对于连续时间控制，采用拉普拉斯变换得到传递函数，进行频域分析。对于离散时间控制，采用z变换得到传递函数进行分析

拉普拉斯变换是连续时间信号分析的核心工具，用于将连续域的 “微分方程” 转化为复频域的 “代数方程”，解决连续系统（如模拟电路、机械系统）的分析问题。关于拉普拉斯变换可以看傅里叶变换和拉普拉斯变换
z变换：z 变换是离散时间信号（序列） 分析的核心数学工具，类比于连续时间信号的拉普拉斯变换，其核心作用是将离散域的 “差分方程” 转化为复频域的 “代数方程”，大幅简化离散系统的分析（如稳定性、频率响应、滤波设计）。
z 变换的本质是 “将离散序列分解为复指数序列的加权和”：

现代控制理论中，对被控系统进行建模，得到一个状态空间模型，与经典运动控制算法相比，现代控制理论可以处理多输入多输出MIMO系统。
现代控制理论与经典控制理论核心区别源于对系统的描述方式、数学工具、研究对象及设计目标的不同。经典控制理论聚焦“输入-输出”的外部特性，现代控制理论则深入“状态”的内部机制，二者并非替代关系，而是适用于不同复杂度的系统场景。

对比维度	经典控制理论（20世纪40-50年代）	现代控制理论（20世纪60年代后，以卡尔曼滤波、庞特里亚金原理为标志）
1. 系统描述模型	基于“输入-输出”的传递函数模型（复频域，拉普拉斯变换导出） 本质是“黑箱/灰箱”模型，不考虑系统内部状态。	基于“状态-输入-输出”的状态空间模型（时域，线性微分方程组） 本质是“白箱”模型，直接描述内部状态的动态变化。
2. 核心数学工具	复变函数（拉普拉斯变换、傅里叶变换）、复频域分析 辅助工具：根轨迹法、奈奎斯特判据、伯德图。	线性代数（矩阵论、向量空间）、时域微分方程 辅助工具：能控性/能观性理论、变分法、庞特里亚金极小值原理、卡尔曼滤波。
3. 研究对象范围	仅限单输入-单输出（SISO） 、线性时不变（LTI） 系统 无法处理非线性、时变、多变量耦合系统。	支持多输入-多输出（MIMO） 系统，可处理线性时变（LTV） 、非线性系统 对耦合系统（如飞机姿态控制：俯仰/滚转/偏航耦合）的描述更精准。
4. 设计方法特点	经验试凑法：基于工程师经验调整参数（如根轨迹法调增益、频域法加校正装置） 目标是“满足稳定裕度、动态/稳态性能”，无严格最优性。	系统化设计法：基于数学推导的定量设计（如极点配置、LQR最优控制、观测器设计） 目标可定制（如最小能耗、最短时间、鲁棒性最优），设计过程更规范。
5. 关键分析能力	仅分析外部性能： - 稳定性（劳斯判据、奈奎斯特判据） - 动态性能（超调量、调节时间） - 稳态性能（稳态误差）	兼顾外部性能+内部状态分析： - 新增“能控性”（控制输入能否影响所有内部状态）、“能观性”（输出能否反映所有内部状态） - 可分析状态收敛性、抗干扰能力、鲁棒性（应对参数摄动）。
6. 适用场景	简单线性系统：如单电机调速、单回路温度控制、单轴机械臂 工业中“单回路PID控制”是经典理论的典型应用。	复杂系统：如导弹姿态控制（MIMO+时变）、卫星轨道控制（最优能耗）、自动驾驶（多传感器融合+非线性）、多机器人协同 需精准控制内部状态或追求最优性能的场景。

最根本区别：“输入-输出” vs “状态”

• 经典控制理论：只关心“给系统一个输入，会得到什么输出”，比如给电机加10V电压（输入），电机转速达到1000rpm（输出），至于电机内部的电流、温度等状态，完全不考虑。
  例：用传递函数$G(s)=\frac{1000}{s+10}$描述电机转速与电压的关系，无法体现电流变化。

• 现代控制理论：必须明确“系统内部有哪些关键状态”，并通过状态方程描述状态的变化规律。
  例：电机的状态包括“转速 ( \omega )”和“电枢电流 ( i )”，状态方程为：
  $$\{\begin{array}{l}\dot{\omega }=-k_1\omega +k_{2}i\\ \dot{i}=-k_{3}i+k_{4}u\end{array}$$
  $u$ 为输入电压，$k_1,k_2,k_3,k_4$为电机参数），输出方程可设为 $y=\omega$（仅输出转速）。

设计逻辑：“经验调参” vs “定量最优”

• 经典控制：设计依赖工程师经验。比如用根轨迹法设计控制器时，需要反复调整增益，让闭环极点落在“期望的性能区域”（如阻尼比0.4~0.8，无超调或小超调），过程是“试凑+验证”。
• 现代控制：设计基于严格的数学优化。比如用LQR（线性二次型调节器） 设计时，只需定义“性能指标”（如“转速误差平方+控制电压平方的积分最小”，即兼顾精度和能耗），通过求解黎卡提方程可直接得到最优控制律，无需试凑。

适用边界：“简单单变量” vs “复杂多变量”

• 经典控制面对多变量系统（如飞机的俯仰、滚转、偏航三个通道耦合）时，会出现“耦合干扰”——调整一个输入，多个输出都会变化，无法独立控制，因此完全失效。
• 现代控制通过状态空间模型可直接描述耦合关系，再通过“解耦控制”或“状态反馈”消除耦合，比如飞机姿态控制中，通过状态反馈矩阵同时调整三个通道的控制量，实现独立稳定。

经典控制是现代控制的“特例”：当系统为SISO-LTI(单输入单输出时不变系统)时，状态空间模型可通过拉普拉斯变换导出传递函数，即经典控制的模型是现代控制模型的“输入-输出投影”。工程中常结合使用：复杂系统的局部简单回路（如卫星的温度控制子回路）仍用经典PID（简单、可靠），而整体姿态控制（多变量耦合）用现代控制（如状态反馈+观测器）。

经典控制理论

经典控制的主要工具是传递函数，方框图，奈奎斯特图以及伯德图。所有工具均围绕 “LTI 系统的稳定性、动态性能、稳态性能” 三大核心目标展开。主要从频域和时域分析展开。

频域分析

频域分析通过系统对不同频率正弦输入的响应（幅频特性、相频特性），间接评估稳定性与性能，核心工具如下：

频率特性（Frequency Response）

对于LTI系统，输入正弦信号，输出的频率不会发生变化，但是幅值和相位可能会发生变化。
系统对正弦输入的稳态响应：若输入为$u(t)=A\sin (\omega t)$，则输出稳态为$y(t)=A\cdot A(\omega )\cdot \sin (\omega t+\phi (\omega ))$，幅值和相位的变化等同于将传递函数的$s$换为$j\omega$(证明自查)，即：$y(t)=A\cdot |G(j\omega )|\cdot \sin (\omega t+\angle G(j\omega ))$其中：

• 幅频特性：$|G(j\omega )|$，表示输出与输入的幅值比随频率$\omega$的变化（反映系统对不同频率信号的“放大/衰减能力”）。
• 相频特性：$\angle G(j\omega )$，表示输出与输入的相位差随频率$\omega$的变化（反映系统对不同频率信号的“延迟能力”）。

伯德图（Bode Plot）

将幅频特性和相频特性分别绘制的对数坐标图，是工程上最常用的频域工具：

• 幅频特性图：纵轴为$20\lg |G(j\omega )|$（单位：dB），横轴为$\lg \omega$（单位：rad/s）
  • 采用对数刻度可将“串联系统的幅频特性”转化为“分贝值相加”，大幅简化计算。$$\begin{array}{rl}L(\omega )& =20\lg |G(j\omega )|=20\lg |G_1(j\omega )G_1(j\omega )\cdots G_n(j\omega )|\\ & =L_1(\omega )+L_2(\omega )+\cdots +L_n(\omega )\end{array}$$
• 相频特性图：纵轴为$\angle G(j\omega )$（单位：°），横轴与幅频图一致。
• 核心应用：
  • 读取增益裕量（GM）：系统达到临界稳定时，幅频特性需额外衰减的分贝值（GM>0dB表示稳定）。
  • 读取相位裕量（PM）：系统达到临界稳定时，相频特性需额外滞后的相位值（PM>0°表示稳定）。
  • 快速设计校正装置（如超前校正、滞后校正），通过调整伯德图形状改善稳定性和性能。

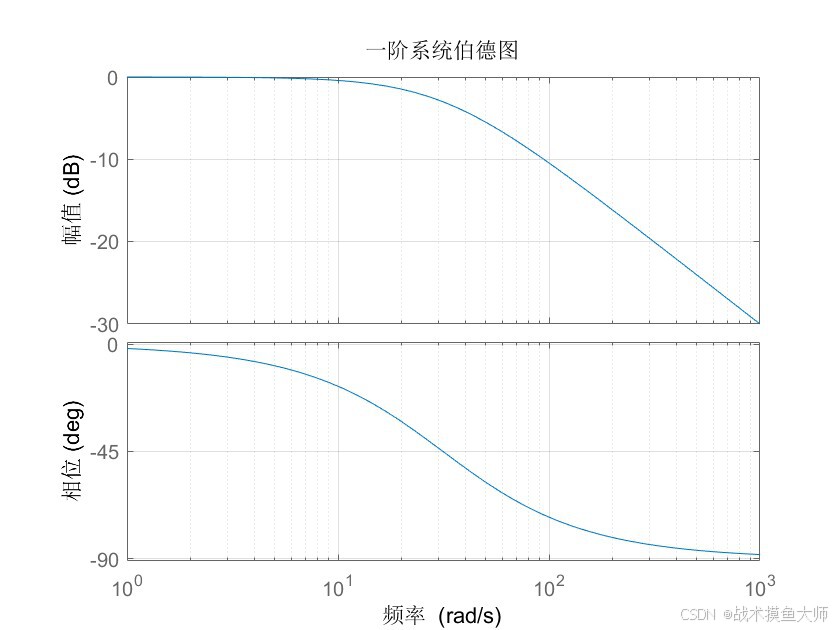
使用matlab画一个一阶系统的伯德图

RC = 0.0318;       % 增益
omega0 = 1;  % 自然频率，例如1 rad/s% 创建传递函数 H(s) = 1/(RCs + omega0)
sys = tf(1, [RC, omega0]);
bode(sys);
% 奈奎斯特图将这个函数改为nyquist(sys)即可
grid on; % 添加网格线以增强可读性
title('一阶系统伯德图');

奈奎斯特图（Nyquist Plot）

在复平面（G(jω)平面） 上，当频率$\omega$从0→∞时，幅频特性和相频特性的轨迹曲线，是判断反馈系统稳定性的核心工具：

• 原理：基于奈奎斯特稳定判据：系统闭环稳定的充要条件是“奈奎斯特曲线绕(-1,j0)点的次数$N$”满足$Z=P-N$（其中$P$为开环系统右半s平面极点个数，$Z$为闭环系统右半s平面极点个数；需$Z=0$时系统稳定）。
• 适用场景：
  • 分析“非最小相位系统”（存在右半s平面零点的系统），伯德图对此类系统的稳定性判断易出错，奈奎斯特图更可靠。
  • 评估系统的“相对稳定性”（增益裕量、相位裕量可通过奈奎斯特图直观读取）。

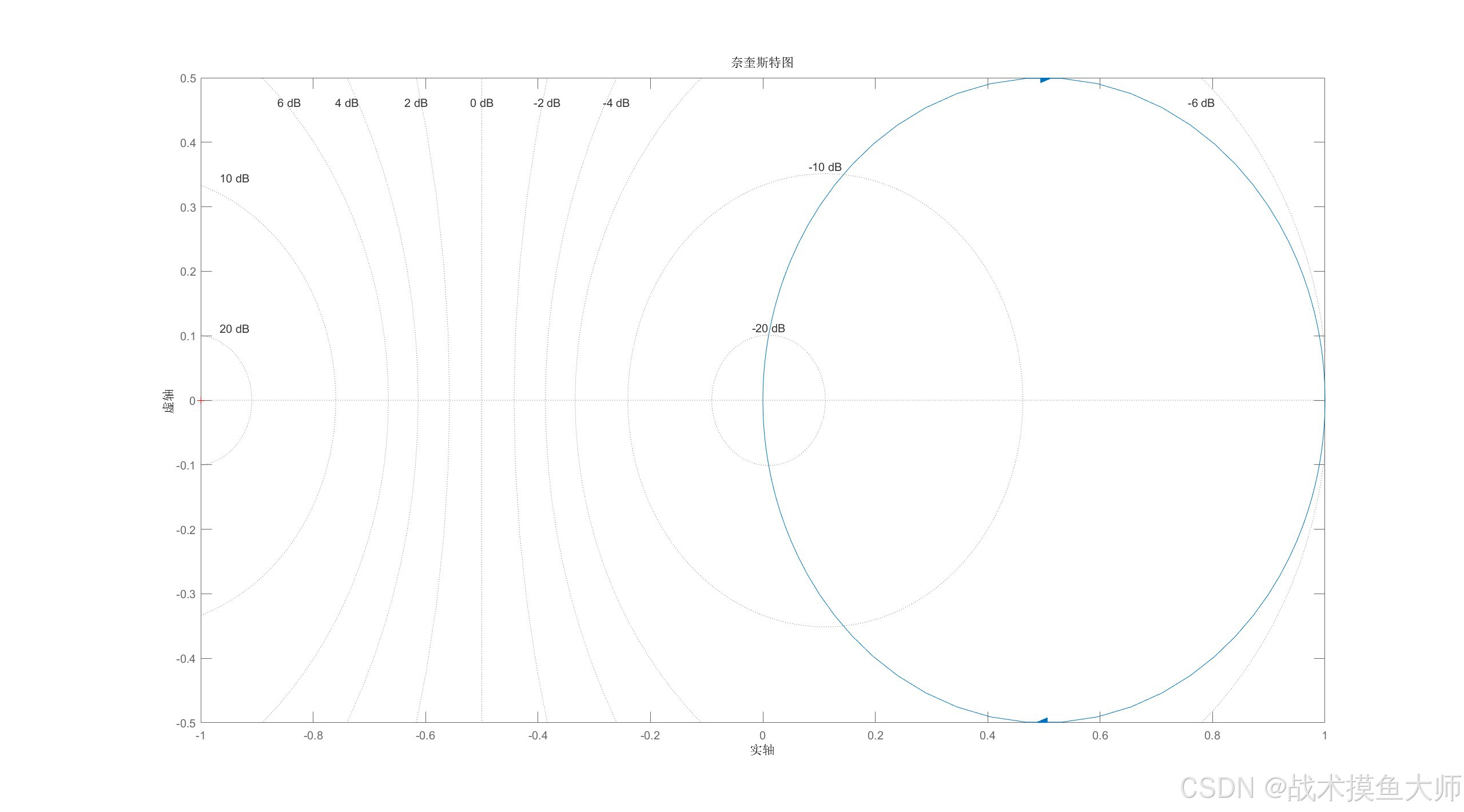
一阶系统的奈奎斯特图：

尼科尔斯图（Nichols Plot）

将幅频特性和相频特性合并绘制在“幅值-相位”坐标上的图形，纵轴为$20\lg |G(j\omega )|$（dB），横轴为$\angle G(j\omega )$（°）：

• 核心优势：可直接叠加“闭环幅频特性曲线”，快速读取闭环系统的“谐振峰值”（反映振荡程度）、“带宽”（反映响应速度），便于闭环性能设计。
• 适用场景：需同时优化开环稳定性和闭环动态性能的场景（如精密伺服系统设计）。

时域分析

时域分析通过系统对典型输入信号（阶跃、斜坡、脉冲） 的输出响应，直接评估系统的 “动态性能”（如超调量、调节时间）和 “稳态性能”（如稳态误差），核心工具如下：

典型输入信号

是时域分析的“标准测试信号”，用于统一评价不同系统的性能：

• 单位阶跃信号（$u(t)$）：输入突然从0变为1并保持，模拟“系统承受恒定扰动或设定值突变”（如电机转速从0突然设定为1000rpm），是最常用的测试信号。
• 单位斜坡信号（$r(t)=t$）：输入随时间线性增长，模拟“系统跟踪缓慢变化的设定值”（如机床进给速度匀速提升）。
• 单位脉冲信号（$\delta (t)$）：输入瞬间产生一个冲量后消失，用于推导系统的“单位脉冲响应”（时域特性的核心指标）。

核心分析指标

基于“单位阶跃响应”定义，直接反映系统性能：

• 动态性能：超调量（$\sigma \%$，反映响应的振荡程度）、调节时间（$t_s$，反映响应的快速性）、上升时间（$t_r$，反映响应的初始速度）。
• 稳态性能：稳态误差（$e_{ss}$，反映系统跟踪设定值的精度），可通过“稳态误差系数”（位置系数$K_p$、速度系数$K_v$、加速度系数$K_a$）快速计算。

劳斯稳定判据（Routh Criterion）

无需求解特征方程根，仅通过特征多项式系数判断系统稳定性：

• 原理：将特征多项式系数按行排列成“劳斯阵列”，若阵列第一列所有元素均为正，则系统稳定；若存在负元素，负元素的个数等于“右半s平面极点的个数”（极点在右半平面时系统不稳定）。
• 适用场景：快速判断低阶系统（如2阶、3阶）的稳定性，或设计控制器时约束参数范围（如确定PID的比例系数上限）。

根轨迹

根轨迹是当系统中某一参数（如PID的比例系数$K_p$）从0→∞变化时，闭环系统极点在s平面上的运动轨迹，核心工具为“根轨迹法”（Root Locus Method），由埃文斯（Evans）提出：

核心原理

基于“开环传递函数极点、零点”与“闭环极点”的关系：闭环特征方程为$1+G(s)H(s)=0$，即$G(s)H(s)=-1$，分解为幅值条件（$|G(s)H(s)|=1$）和相位条件（$\angle G(s)H(s)=\pm (2k+1)\pi$，$k=0,1,\mathrm{2...}$）。根轨迹需满足相位条件，幅值条件用于确定轨迹上某点对应的参数值。

总结：经典控制理论工具的核心逻辑

所有工具均围绕“LTI系统的稳定性、动态性能、稳态性能”三大核心目标展开，不同工具的适用场景各有侧重：

• 若需快速判断稳定性：优先用劳斯判据（低阶）或奈奎斯特图（高阶/非最小相位系统）。
• 若需设计控制器参数：优先用根轨迹法（明确极点位置）或伯德图（频域性能直观）。
• 若需直观描述系统组成：用方框图或信号流图；若需定量计算响应：用传递函数（频域/根轨迹）或微分方程（时域）。

这些工具共同构成了经典控制理论的“分析与设计体系”，至今仍是工业控制（如PID控制、电机调速、过程控制）的核心技术基础。

经典控制理论案例

以一个简单的一阶系统为例，演示如何使用经典控制理论。
设计一个低通滤波，用于过滤高频信号

滤波的本质是“对不同频率的信号进行选择性衰减”：低通滤波器（LPF） 允许低频信号（包括直流）通过，而抑制高频信号。RC串联电路通过“电容容抗随频率变化”的特性，天然实现了这一功能。

RC串联电路是电子系统中最基础的动态电路之一，其核心特性由时间常数$\tau =RC$ 和容抗的频率依赖性决定；当以“电容电压为输出”时，它天然成为低通滤波器，通过选择性衰减高频信号实现“保留低频、抑制高频”的功能。

一个添加了反馈电阻以及运算放大器的有源RC滤波电路如下，但是原理没有变化。

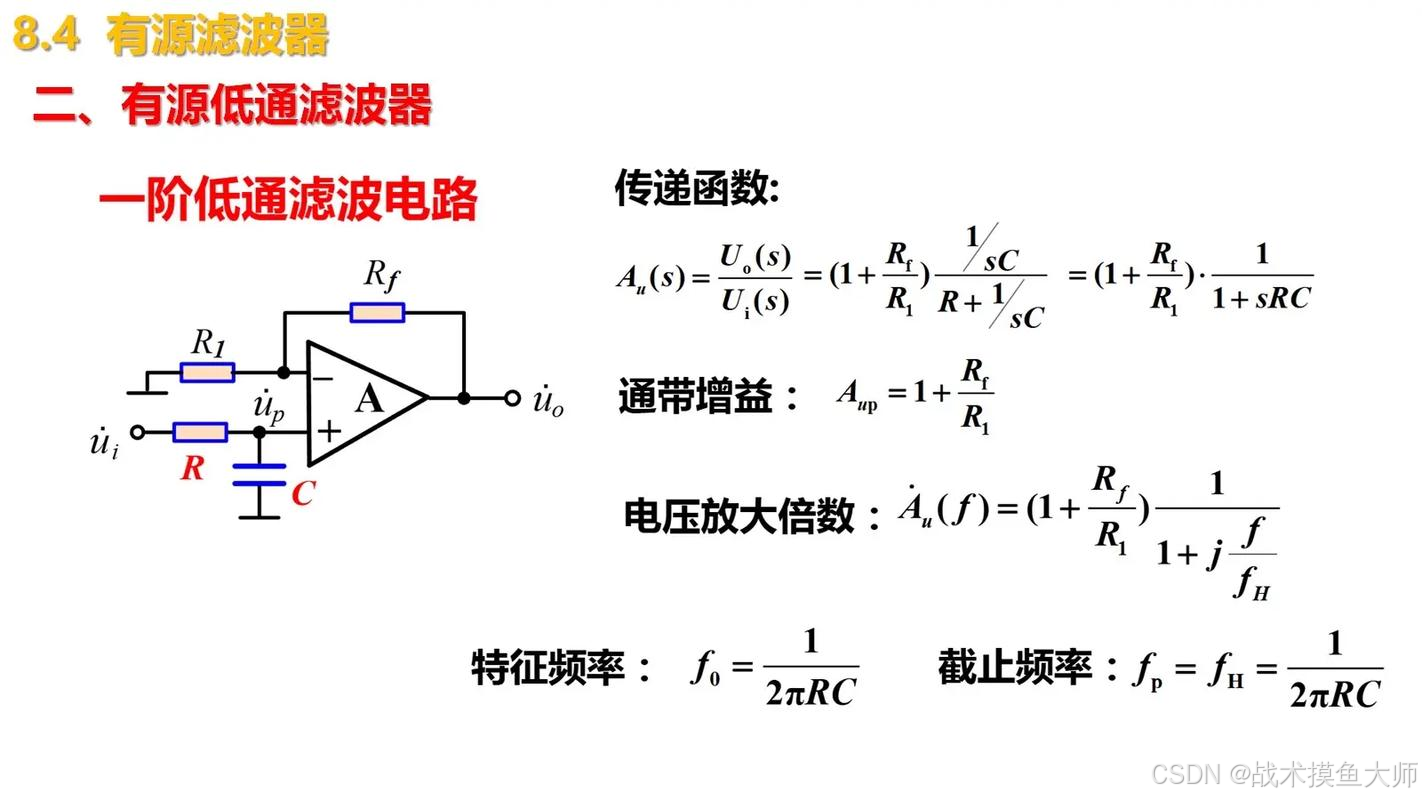
无源滤波器：结构简单，成本低，但存在一些局限性。它的带负载能力差，当后续电路的输入阻抗较低时，会影响滤波效果；而且没有放大能力，信号经过滤波后可能会有衰减，对于需要信号放大的场景不适用。
有源滤波器：由于引入了运算放大器，具备有源器件的优势。运算放大器的高输入阻抗使得它对前级 RC网络的影响很小，带负载能力强；同时通过反馈电阻可以实现信号的放大，能更好地满足对信号幅值和驱动能力的要求，性能更优，适用场景更广泛。

传递函数推导

传递函数$G(j\omega )$定义为“输出电压的傅里叶变换与输入电压的傅里叶变换之比”，反映电路对不同角频率$\omega =2\pi f$ 信号的衰减能力。

在交流稳态下，元件的电压电流关系需用“复数阻抗”表示：

• 电阻的复数阻抗：$Z_R=R$（与频率无关）；
• 电容的复数阻抗：$Z_C=\frac{1}{j\omega C}$（$j$ 为虚数单位，体现相位滞后）；
• 串联总阻抗：$Z_{总}=Z_R+Z_C=R+\frac{1}{j\omega C}$。

根据“分压原理”，输出电压$U_o(j\omega )=U_C(j\omega )=I(j\omega )\cdot Z_C$，输入电压$U_i(j\omega )=I(j\omega )\cdot Z_{总}$，因此传递函数为：
$$G(j\omega )=\frac{U_o(j\omega )}{U_i(j\omega )}=\frac{Z_C}{Z_R+Z_C}=\frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}}$$

化简后得到：
$$G(j\omega )=\frac{1}{1+j\omega RC}=\frac{1}{1+j\frac{\omega }{{\omega }_c}}$$
其中${\omega }_c=\frac{1}{RC}$ 称为截止角频率，对应的截止频率（常用单位：Hz）为$f_c=\frac{{\omega }_c}{2\pi }=\frac{1}{2\pi RC}$——这是低通滤波器的“核心指标”，定义了“通频带”与“阻带”的分界。

幅频特性：信号衰减的量化

传递函数的模（幅值） 表示输出信号相对于输入信号的衰减比例，公式为：
$$|G(j\omega )|=\frac{1}{\sqrt{1+{\left(\frac{\omega }{{\omega }_c}\right)}^2}}$$

频率范围	与截止频率的关系	幅频特性	物理意义（滤波效果）
低频段（$f\ll f_c$）	$\frac{\omega }{{\omega }_c}\ll 1$	$\approx 1$（衰减0dB）	信号几乎无衰减，顺利通过（通带）
截止频率点（$f=f_c$）	$\frac{\omega }{{\omega }_c}=1$	$\frac{1}{\sqrt{2}}\approx 0.707$（衰减-3dB）	信号功率衰减50%，定义通带边界
高频段（$f\gg f_c$）	$\frac{\omega }{{\omega }_c}\gg 1$	$\approx \frac{1}{\frac{\omega }{{\omega }_c}}=\frac{1}{2\pi fRC}$（衰减随频率增大）	信号大幅衰减，被抑制（阻带）

• 对低频信号（如50Hz市电、音频信号中的低音），电容容抗大，大部分电压降在电容上（输出大）；
• 对高频信号（如电磁干扰、射频噪声），电容容抗小，大部分电压降在电阻上（输出小，被过滤）。

相位特性：信号的“时间延迟”

除了幅值衰减，RC低通滤波器还会导致信号相位滞后（输出信号比输入信号“慢”一点），这是电容“电压滞后电流90°”的特性导致的。

传递函数的相位角公式为：
$$\angle G(j\omega )=-\arctan \left(\frac{\omega }{{\omega }_c}\right)$$

• 当$f\to 0$（直流）：相位滞后$\to 0°$（无延迟）；
• 当$f=f_c$（截止频率）：相位滞后$=-45°$（固定值）；
• 当$f\to \infty$（高频）：相位滞后$\to -90°$（最大延迟）。

相位滞后在实际应用中需注意（如音频系统中可能导致音质失真，控制系统中可能影响稳定性），但对单纯的“噪声过滤”场景（如电源去耦）影响较小。

关键设计参数：如何选择R和C？

RC低通滤波器的核心是确定截止频率$f_c$，再根据实际电路约束选择R和C的数值，步骤如下：

1. 确定截止频率$f_c$：
   根据“需要保留的最高频率”确定$f_c$（通常取通带最高频率的1.2~1.5倍，避免边缘信号衰减过多）。例如：

   • 滤除电源高频噪声（需保留直流，抑制100kHz以上噪声）：取$f_c=10kHz$；
   • 音频滤波（需保留20Hz~20kHz）：取$f_c=20kHz$。

2. 推导R和C的关系：
   由$f_c=\frac{1}{2\pi RC}$，可得$RC=\frac{1}{2\pi f_c}$。只需确定其中一个参数，即可计算另一个。

3. 选择R和C的具体数值：

   • 电阻R：通常选择1kΩ~100kΩ（过小会导致电路电流过大，功耗增加；过大则容易引入外界干扰，且输出阻抗高，不适合驱动负载）；
   • 电容C：根据R的取值计算，优先选择常用容值（如1nF、10nF、100nF、1μF），避免使用特殊容值（成本高、难采购）。

设计实例：例如需设计一个$f_c=50Hz$ 的RC低通滤波器。

• 计算$RC=\frac{1}{2\pi f_c}=3.183ms$
• 选择R：电阻 R 的选择需兼顾 “电路阻抗匹配” 和 “信号损耗”，工程上 RC 低通滤波器的 R 通常选择$1k\Omega$到$100k\Omega$范围，根据RC值，选用$1k\Omega$；
• 计算C：$C=\frac{1}{2\pi f_{c}R}=\frac{1}{2\times 3.14\times 50\times 10^3}\approx 3.183\mu F$，取常用值3.3nF（误差在5%以内，工程上可接受）。
  使用matlab的Simulink进行仿真：
  
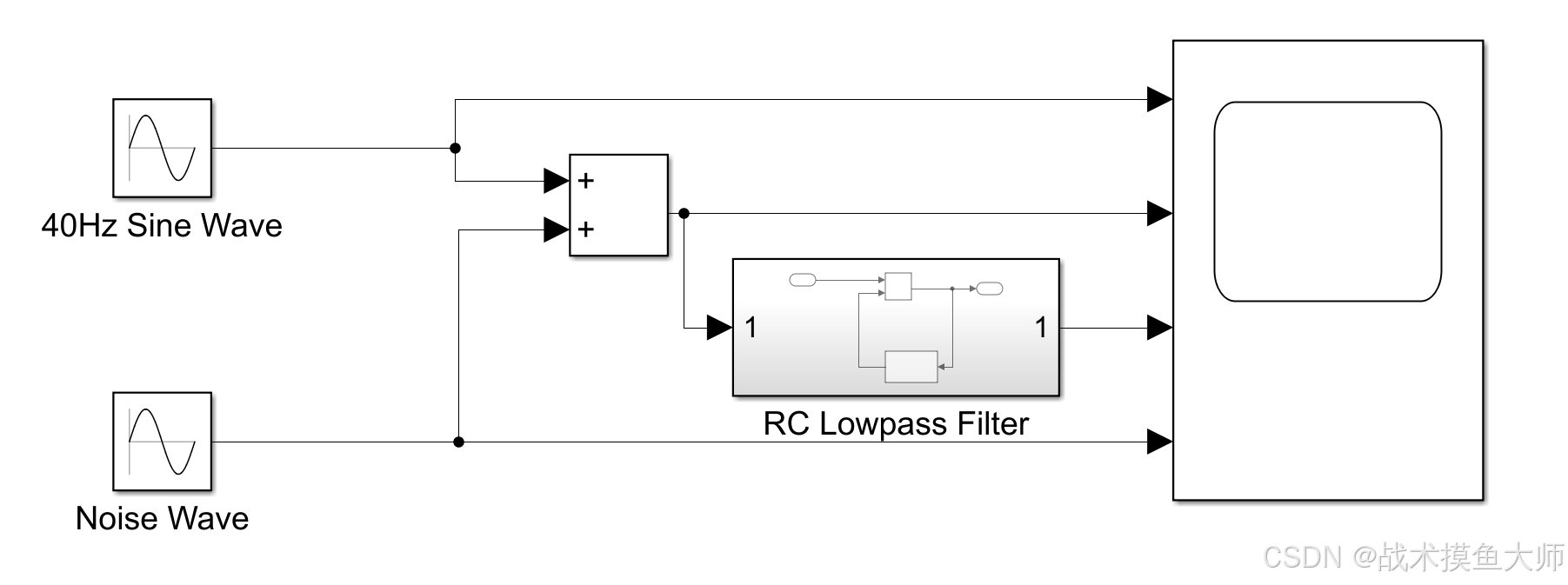
  其中的RC滤波根据RC的微分方程实现如下：
  

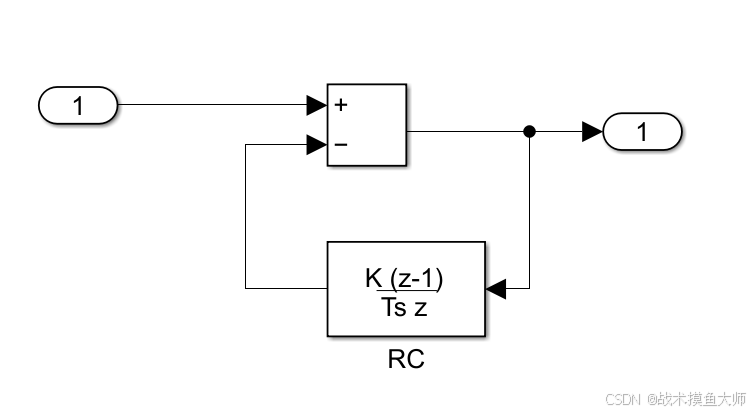
也可以使用simulink中的传递函数模块，结果一样的。

仿真结果如下：

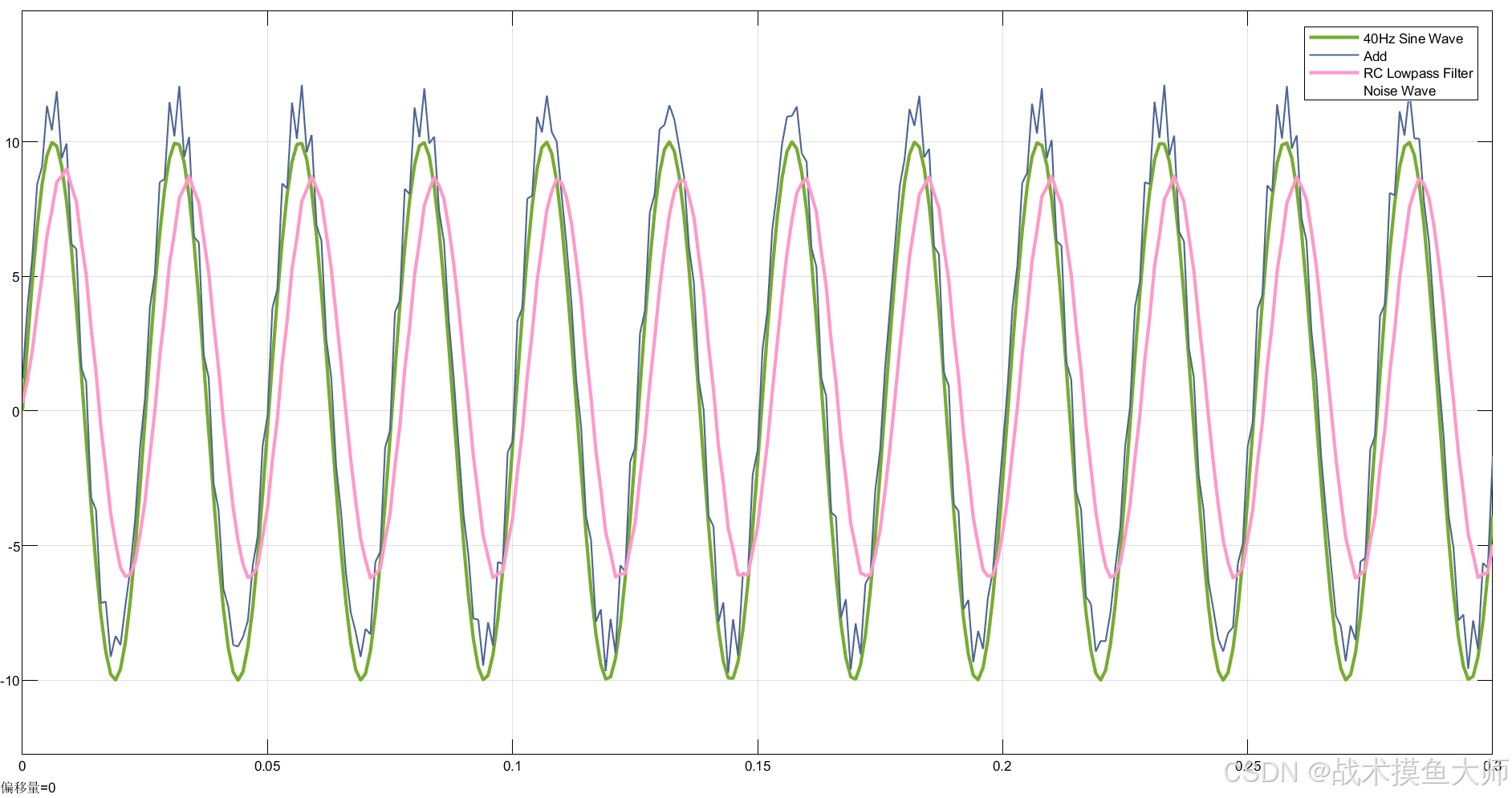
其中绿色为期望信号，粉色为滤波后信号，蓝色为带有噪音的原始信号。

现代控制理论

现代控制理论的工具主要集中在：建模，系统分析，观测，控制，四个方面。

建模

状态空间表达式（核心）

• 核心思想：用“状态变量”（描述系统内部行为的最小变量集，如RC电路的电容电压、电机的转速/转角）完整刻画系统动态，将高阶微分方程转化为一阶线性微分方程组（线性系统）或非线性方程组（非线性系统）。
• 数学形式（连续时间线性时不变系统，LTI）：
  $$\{\begin{array}{l}\dot{\mathbf{x}}(t)=\mathbf{Ax}(t)+\mathbf{Bu}(t)\text{（状态方程：描述内部动态）}\\ \mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{Du}(t)\text{（输出方程：描述外部观测）}\end{array}$$
  其中：
  • $\mathbf{x}(t)\in {\mathbb{R}}^n$：状态向量（$n$ 为系统阶数）；
  • $\mathbf{u}(t)\in {\mathbb{R}}^p$：输入向量（$p$ 为输入个数）；
  • $\mathbf{y}(t)\in {\mathbb{R}}^q$：输出向量（$q$ 为输出个数）；
  • $\mathbf{A}(n\times n)、\mathbf{B}(n\times p)、\mathbf{C}(q\times n)、\mathbf{D}(q\times p)$：系统矩阵、输入矩阵、输出矩阵、直接传输矩阵。
• 应用场景：所有现代控制工具的“输入”，无论是稳定性分析、能控性判断还是控制器设计，均基于此表达式。例如：直流电机可建模为 $n=2$ 的系统（状态：转速 $\omega$、电枢电流 $i_a$）。

传递函数矩阵（多变量系统扩展）

• 核心思想：线性系统在拉普拉斯变换下，输入与输出的“传递关系矩阵”，是经典控制理论“单变量传递函数”的多变量推广。
• 数学形式：对状态空间表达式取拉普拉斯变换（零初始条件），得 $\mathbf{G}(s)=\mathbf{C}(s\mathbf{I}-\mathbf{A}{)}^{-1}\mathbf{B}+\mathbf{D}$，其中 $\mathbf{G}(s)\in {\mathbb{R}}^{q\times p}$ 是传递函数矩阵，每个元素 $G_{ij}(s)$ 表示第 $j$ 个输入对第 $i$ 个输出的传递关系。
• 作用：连接经典控制与现代控制，方便分析多变量系统的输入输出特性（如耦合性）。

约旦标准型（系统简化工具）

• 核心思想：通过相似变换（$\mathbf{x}=\mathbf{Tz}$，$\mathbf{T}$ 为可逆变换矩阵），将系统矩阵 $\mathbf{A}$ 转化为“约旦标准型”（对角矩阵或含约旦块的矩阵），暴露系统的“模态特性”（每个模态对应一个极点）。
• 作用：简化系统分析（如稳定性、能控能观性）和控制器设计（如极点配置），因为约旦标准型的结构更清晰（对角元素为系统极点）。

系统分析

稳定性分析

稳定性是系统正常工作的首要条件，现代控制理论提供了适用于线性/非线性、定常/时变系统的稳定性判据，核心是李雅普诺夫方法。

线性系统的特征值判据（李雅普诺夫第一方法特例）

• 适用场景：线性时不变（LTI）系统。
• 核心原理：LTI系统的稳定性由系统矩阵 $\mathbf{A}$ 的特征值决定：
  • 若所有特征值的实部均小于0（即 $\text{Re}({\lambda }_i)<0$），系统渐近稳定（最终收敛到平衡态）；
  • 若存在特征值实部≥0，系统不稳定或临界稳定。
• 优势：直观、计算简单（通过求解 $\det (s\mathbf{I}-\mathbf{A})=0$ 得特征值）；
• 局限：仅适用于线性系统，无法处理非线性或时变系统。

李雅普诺夫稳定性理论（核心，适用于所有系统）

• 核心思想：类比“物理系统的能量衰减”——若能找到一个“能量函数”（李雅普诺夫函数 $V(\mathbf{x})$），满足：
  1. $V(\mathbf{x})>0$（正定，能量非负，仅平衡态为0）；
  2. $\dot{V}(\mathbf{x})=\frac{dV}{dt}<0$（负定，能量随时间衰减）；
     则系统在平衡态处渐近稳定。
• 两大方法：
  • 李雅普诺夫第一方法（间接法）：通过线性化非线性系统，用线性系统的特征值判据分析原非线性系统的局部稳定性（仅适用于平衡态附近）；
  • 李雅普诺夫第二方法（直接法）：无需求解系统微分方程，直接构造 $V(\mathbf{x})$ 分析稳定性，适用于线性/非线性、定常/时变系统，且可分析全局稳定性（整个状态空间）。
• 应用场景：非线性系统（如机械臂、化工反应过程）的稳定性分析，是现代控制中非线性控制设计的基础（如反步法设计需构造李雅普诺夫函数）。

输入输出稳定性（鲁棒性初步分析）

• 核心思想：针对“存在扰动或不确定性”的系统，分析输入（如扰动）有界时，输出是否也有界（BIBO稳定：有界输入→有界输出）。
• 关键工具：小增益定理（$\Vert \mathbf{G}(s){\Vert }_{\infty }<1$，即系统的H∞范数小于1，保证闭环系统BIBO稳定），是鲁棒控制的基础。

能控性与能观性分析

能控性决定“是否能通过输入改变系统状态”，能观性决定“是否能通过输出估计系统状态”，是状态反馈控制器和观测器设计的前提（卡尔曼提出，现代控制理论的里程碑）。

• 能控性：对任意初始状态 $\mathbf{x}(t_0)$ 和任意目标状态 $\mathbf{x}(t_1)$，是否存在输入 $\mathbf{u}(t)$（$t_0\le t\le t_1$），使系统从 $\mathbf{x}(t_0)$ 转移到 $\mathbf{x}(t_1)$（完全能控）。
• 能观性：对任意初始状态 $\mathbf{x}(t_0)$，是否能通过观测有限时间内的输出 $\mathbf{y}(t)$（$t_0\le t\le t_1$），唯一确定 $\mathbf{x}(t_0)$（完全能观）。

卡尔曼秩判据（最常用的判据）

• 能控性秩判据：LTI系统完全能控的充要条件是“能控性矩阵”的秩等于系统阶数 $n$：
  $$\text{rank}({\mathbf{C}}_c)=n,\text{其中 }{\mathbf{C}}_c=\left[\mathbf{B}\mathbf{AB}{\mathbf{A}}^2\mathbf{B}\dots {\mathbf{A}}^{n-1}\mathbf{B}\right]$$
• 能观性秩判据：LTI系统完全能观的充要条件是“能观性矩阵”的秩等于 $n$：
  $$\text{rank}({\mathbf{C}}_o)=n,\text{其中 }{\mathbf{C}}_o={\left[{\mathbf{C}}^T{\mathbf{A}}^T{\mathbf{C}}^T({\mathbf{A}}^T{)}^2{\mathbf{C}}^T\dots ({\mathbf{A}}^T{)}^{n-1}{\mathbf{C}}^T\right]}^T$$
• 示例：RC低通滤波器（$n=1$，状态为电容电压 $x$），输入 $u$ 为电源电压，状态方程 $\dot{x}=-\frac{1}{RC}x+\frac{1}{RC}u$（即 $\mathbf{A}=-\frac{1}{RC}$，$\mathbf{B}=\frac{1}{RC}$）。能控性矩阵 ${\mathbf{C}}_c=[\mathbf{B}]=\frac{1}{RC}\ne 0$，秩为1（等于 $n=1$），故完全能控。

结构分解与对偶原理

• 结构分解：将不完全能控/能观的系统，分解为“能控+不能控”“能观+不能观”的子系统（如能控分解、能观分解），仅需对“能控能观子系统”设计控制器，简化设计复杂度。
• 对偶原理：系统 $(\mathbf{A},\mathbf{B},\mathbf{C})$ 的能控性等价于其对偶系统 $({\mathbf{A}}^T,{\mathbf{C}}^T,{\mathbf{B}}^T)$ 的能观性，反之亦然。该原理减少了分析量（只需分析能控性，可推导能观性）。

鲁棒性分析

实际系统存在参数摄动（如电阻电容误差）、外部扰动（如噪声），鲁棒性分析工具用于判断系统在这些不确定性下是否仍稳定、性能是否满足要求。

• 核心工具：
  1. H∞范数分析：用H∞范数（系统对扰动的最大放大倍数）衡量鲁棒性，$\Vert \mathbf{G}(s){\Vert }_{\infty }$ 越小，系统抗扰动能力越强；
  2. 结构奇异值（μ分析）：针对“结构化不确定性”（如参数摄动的特定形式），判断闭环系统的鲁棒稳定性，比H∞分析更精准。

观测器

实际系统中，状态往往无法全部直接测量（如电机的电磁转矩难以直接测），观测器的作用是通过“可测量的输出”估计“不可测量的状态”，为状态反馈提供“虚拟状态”。设计需满足“能观”的前提。

观测器建立在能观性的基础上，如果无法观测，那就只有输入输出，跟经典控制理论也没区别了。观测器的博客

全维观测器（Full-Order Observer）

• 核心思想：构造一个与原系统“结构相同”的动态系统（观测器），通过“输出误差”（原系统输出 $\mathbf{y}$ 与观测器输出 $\hat{\mathbf{y}}$ 的差值）修正观测器的状态 $\hat{\mathbf{x}}$，使 $\hat{\mathbf{x}}$ 逐步收敛到真实状态 $\mathbf{x}$。
• 观测器方程：
  $$\dot{\hat{\mathbf{x}}}=\mathbf{A}\hat{\mathbf{x}}+\mathbf{Bu}+\mathbf{L}(\mathbf{y}-\hat{\mathbf{y}})=(\mathbf{A}-\mathbf{LC})\hat{\mathbf{x}}+\mathbf{Bu}+\mathbf{Ly}$$
  其中 $\mathbf{L}$ 是观测器增益矩阵，$\hat{\mathbf{x}}$ 是估计状态，$\hat{\mathbf{y}}=\mathbf{C}\hat{\mathbf{x}}$ 是估计输出。
• 设计关键：通过配置观测器闭环矩阵 $\mathbf{A}-\mathbf{LC}$ 的极点（要求收敛速度比闭环系统快2~5倍，避免观测误差影响控制），确定 $\mathbf{L}$。
  （注：由对偶原理，观测器增益 $\mathbf{L}$ 的设计等价于“对偶系统的状态反馈增益”设计，可复用极点配置或LQR方法。）

降维观测器（Reduced-Order Observer）

• 核心思想：若系统部分状态可直接测量（如电机的转速可通过编码器测，属于可观测输出），则仅需估计“不可测量的状态”，减少观测器的阶数（从 $n$ 阶降至 $n-q$ 阶，$q$ 为输出个数），简化硬件实现。
• 典型代表：龙伯格观测器（Luenberger Observer），通过状态分解（将状态分为“可测部分 ${\mathbf{x}}_1$”和“不可测部分 ${\mathbf{x}}_2$”），仅对 ${\mathbf{x}}_2$ 设计观测器。
• 优势：降低计算复杂度和硬件成本，适用于嵌入式控制系统（如单片机、FPGA）。

卡尔曼滤波器（Kalman Filter）

可以理解为：卡尔曼观测器针对于不确定系统，龙伯格观测器或者其他观测器都是针对确定系统。至于完全不确定的系统，可以使用粒子滤波来处理，这就是另一方面的事情了。

• 核心思想：针对“存在过程噪声（如系统扰动）和测量噪声（如传感器误差）”的系统，设计最优观测器，使状态估计误差的方差最小（即“最小方差估计”）。
• 适用场景：带噪声的线性系统（连续或离散），如导航系统（GPS+IMU融合）、自动驾驶（激光雷达+摄像头数据融合）、工业过程检测（传感器噪声滤波）。
• 核心步骤（离散卡尔曼滤波器）：
  1. 预测步：根据上一时刻估计状态，预测当前时刻状态和误差协方差；
  2. 更新步：利用当前时刻测量输出，修正预测状态，更新误差协方差（卡尔曼增益 ${\mathbf{K}}_k$ 决定修正权重）。
• 与普通观测器的区别：普通观测器假设无噪声，仅通过输出误差修正；卡尔曼滤波器量化噪声统计特性（过程噪声协方差 $\mathbf{Q}$、测量噪声协方差 $\mathbf{R}$），实现最优估计。

先进控制

针对非线性、时变、多约束、强耦合的复杂系统，现代控制理论衍生出更先进的工具，突破线性系统的限制。

鲁棒控制器设计（H∞控制、滑模控制）

• H∞控制：针对“结构化/非结构化不确定性”，设计控制器使闭环系统的H∞范数小于指定值，保证鲁棒稳定性和鲁棒性能（如扰动抑制），适用于化工过程、机器人等参数易变的系统。
• 滑模控制（SMC）：通过设计“变结构控制律”，使系统状态强制收敛到“滑模面”，并沿滑模面稳定到平衡态。对参数摄动和外部扰动有强鲁棒性（不敏感），适用于电机控制、无人机抗干扰控制。

模型预测控制（MPC：Model Predictive Control）

• 核心思想：“滚动优化+反馈校正”——基于预测模型，在每个时刻优化未来有限时域内的控制量（考虑输入/输出约束），仅执行当前时刻的控制量，下一时刻重新优化。
• 优势：能处理多变量、强耦合、有硬约束（如电机电流上限、液位上限）的系统，是工业界应用最广泛的先进控制技术之一；
• 应用场景：化工反应釜温度/压力控制、电力系统调度、自动驾驶路径跟踪。

自适应控制（Adaptive Control）

• 核心思想：针对“参数未知或时变”的系统（如无人机负载变化、电池老化），在线估计未知参数，并实时调整控制器参数，使系统性能保持稳定。
• 典型类型：模型参考自适应控制（MRAC，使系统输出跟踪参考模型输出）、自校正调节器（STR，在线估计系统参数并更新控制器）。

非线性控制工具

• 反馈线性化：通过非线性坐标变换和状态反馈，将非线性系统转化为“线性系统”，再用线性控制方法设计控制器（如机械臂的反馈线性化控制）；
• 反步法（Backstepping）：逐步构造李雅普诺夫函数和控制律，处理“严反馈型”非线性系统（如永磁同步电机的转速控制），保证全局稳定性。

总结：现代控制工具的逻辑链

现代控制理论的工具体系围绕“建模→分析→设计→优化”形成闭环，核心逻辑如下：

1. 用状态空间表达式建立系统模型；
2. 用能控能观性分析判断是否可设计控制器/观测器，用李雅普诺夫方法分析稳定性；
3. 若状态可测，用极点配置/LQR设计状态反馈控制器；若状态不可测，先设计观测器/卡尔曼滤波器估计状态，再结合控制器构成“输出反馈控制器”；
4. 若系统有不确定性、约束或非线性，用H∞控制/MPC/反馈线性化等先进工具优化性能。

前馈控制vs反馈控制

在控制系统中，前馈控制（Feedforward Control） 和 反馈控制（Feedback Control） 是两种核心控制策略，其根本区别在于是否利用“系统输出的偏差”来驱动控制动作——反馈控制依赖“偏差修正”，前馈控制依赖“扰动预判”，二者在控制逻辑、响应速度和适用场景上差异显著，常结合使用以优化控制性能。

对比维度	反馈控制（Feedback Control）	前馈控制（Feedforward Control）
1. 核心控制依据	输出偏差：即“设定值（期望输出） - 实际输出”的差值 只有当输出偏离设定值时，才产生控制动作。	可测扰动：即“影响输出的外部干扰”（如负载变化、电压波动） 无需等待输出偏差，直接根据扰动的大小和方向提前补偿。
2. 控制动作时机	“滞后响应”：偏差出现后才动作（需经历“输出偏离→检测偏差→计算控制量→执行”的过程）。	“超前补偿”：扰动刚发生（甚至未影响输出前），就启动控制动作，抵消扰动对输出的影响。
3. 系统结构	闭环结构：必须包含“传感器（检测输出）→比较器（计算偏差）→控制器→执行器→被控对象”的闭环回路，形成“偏差→修正→再检测”的循环。	开环结构：无需检测输出，仅包含“扰动传感器→前馈控制器→执行器→被控对象”的开环路径，不形成闭环循环。
4. 抗扰动能力	- 对所有影响输出的扰动（无论是否可测）都有修正作用（只要扰动导致输出偏差，就会被闭环检测并修正）。 - 但修正存在滞后，对快速扰动（如电网电压骤降）的抑制效果较差。	- 仅对提前设定的、可测量的特定扰动有效（若扰动不可测或未纳入前馈模型，无法补偿）。 - 补偿无滞后，对已知快速扰动的抑制效果极佳。
5. 控制精度与稳定性	- 精度依赖“偏差检测精度”和“控制器参数设计”，理论上可通过持续修正使偏差趋近于零（如PID控制的无静差特性）。 - 闭环结构可能引入稳定性问题（如参数不当导致系统振荡、超调）。	- 精度完全依赖“前馈模型的准确性”（需精确计算“扰动→输出变化”的关系，若模型误差大，补偿效果会恶化）。 - 开环结构不影响原系统稳定性（仅叠加补偿量，无闭环振荡风险）。
6. 典型应用场景	- 扰动复杂且不确定的场景：如家用空调（室温受开门、日照、人数等多因素影响，无法提前预判所有扰动，依赖反馈修正温差）、工业炉温控制（受燃料压力、环境温度波动影响）。 - 经典应用：PID控制器（所有基于偏差的闭环控制核心）。	- 扰动可测且影响显著的场景：如精密机床（切削负载变化会导致主轴转速下降，通过前馈补偿负载扭矩，维持转速稳定）、电网稳压电源（提前检测输入电压波动，前馈调整稳压电路，避免输出电压偏移）、传送带速度控制（物料重量变化前馈补偿电机扭矩）。

核心差异的深层解读

最根本区别：“偏差驱动” vs “扰动驱动”

这是两者逻辑的本质不同，可通过“水杯倒水”的生活化例子理解：

• 反馈控制：相当于“先倒水，再看水位——如果水位低于目标（偏差），就继续加水；如果高于目标，就倒掉多余的水”。整个过程依赖“水位偏差”的反馈，必然存在“先偏离再修正”的滞后。
  工程实例：家用洗衣机的水位控制——先进水，水位传感器检测实际水位，若低于设定值（偏差），继续进水；若达到设定值，停止进水（反馈闭环修正）。

• 前馈控制：相当于“提前计算‘杯子的容积+当前水量’，知道还需要加多少水，一次性加到位，无需等待水位偏差”。整个过程依赖“扰动（当前水量）的预判”，无滞后。
  工程实例：汽车巡航控制中的“坡度前馈”——当GPS检测到前方上坡（扰动：坡度会导致车速下降），无需等待车速降低（无偏差时），就提前增加发动机扭矩，抵消坡度对车速的影响，维持巡航速度稳定。

“普适性” vs “针对性”

• 反馈控制的优势是“普适”：无论扰动是“可测”（如电网电压变化）还是“不可测”（如环境风干扰），只要扰动导致输出偏差，闭环就会启动修正。但代价是“滞后”——对于快速变化的扰动（如毫秒级的电压骤降），反馈修正的速度可能跟不上扰动的变化，导致输出短暂偏离设定值（即“动态误差”）。

• 前馈控制的优势是“针对性”：对已知的快速扰动，能做到“扰动发生即补偿”，几乎无动态误差。但代价是“局限性”——若扰动不可测（如突发的机械振动），或前馈模型不准确（如计算“负载→转速变化”的系数偏差），前馈不仅无效，还可能引入额外干扰（如过度补偿导致输出超调）。

由于单独使用前馈或反馈都有局限，实际工程中常采用“前馈+反馈”的复合控制，结合两者优势：

• 前馈：负责抵消“已知的、主要的快速扰动”（如机床的切削负载、电网的电压波动），减少反馈控制的负担，避免输出出现大的动态偏差。
• 反馈：负责修正“前馈未补偿的剩余偏差”和“未预见的未知扰动”（如环境温度变化、模型误差），确保输出最终稳定在设定值，实现高精度控制。

控制需求	优先选择反馈控制	优先选择前馈控制（或复合控制）
扰动特点	扰动多、不确定、不可测	扰动可测、影响大、变化快
控制目标	追求长期稳定精度，可接受轻微动态偏差	追求无滞后补偿，抑制快速扰动导致的动态偏差
系统复杂度	被控对象简单，无需复杂模型	被控对象特性明确，可建立准确的“扰动-输出”模型

简言之：“反馈管精度，前馈管速度” ——不确定扰动靠反馈兜底，已知快速扰动靠前馈预判，二者结合是复杂系统高精度控制的核心方案。
以机床主轴转速控制为例：机床切削时，工件硬度变化、进给速度调整、切削深度改变等都会导致切削负载（扰动）波动，而主轴转速的稳定直接决定加工精度（如螺纹加工的螺距精度、铣削的表面粗糙度）—— 若负载增大，主轴电机扭矩不足会导致转速下降，最终使加工尺寸超差。
实际控制中，常用复合控制方案，用前馈控制 “抵消已知的、快速的负载扰动”，用反馈控制 “修正前馈的残留误差和未知扰动”，二者协同实现 “无滞后、无偏差” 的主轴转速控制。

例子

结合现代控制理论以及PID控制的一个例子：
在机床传动系统（如主轴、进给轴）中，可以通过设计状态观测器（基于系统动力学模型和可测变量）来间接估计负载扭矩；
首先进行机电系统（）简化建模：
$$J\cdot \dot{\omega }+B\cdot \omega +T_L=T_M$$
其中各参数含义如下：

参数	物理意义	可测性
$J$	系统总转动惯量（电机+减速箱+主轴+工件）	通常时变/不可直接测量
$\dot{\omega }$	角速度加速度（转速的导数）	不可直接测量（需计算）
$\omega$	主轴（或电机）角速度	可测（通过编码器获取）
$B$	粘性阻尼系数（传动摩擦、油阻等）	近似恒定（可辨识）
$T_L$	切削负载扭矩（待观测的目标量）	不可测（无扭矩传感器）
$T_M$	电机输出扭矩（可间接计算）	可测（通过电机电流计算）

这个建模是非常简化的，实际应用中，大型机床的粘性阻尼系数会随着随电机速度、工作温度、运行时间、润滑油性质的变化而时变，具有非线性特性。

其中的关键可测变量：

• 角速度$\omega$：由电机轴或主轴上的编码器（如光电编码器、光栅尺）实时采集，采样频率通常达kHz级，精度足够；
• 电机输出扭矩$T_M$：对于直流电机或永磁同步电机（PMSM），$T_M$与电枢电流$I_a$（等于q轴定子电流）成正比（$T_M=K_t\cdot I_a$，$K_t$为电机转矩常数，可查手册或辨识），因此通过电流传感器采集$I_a$即可间接得到$T_M$。

接着需要根据可测变量设计观测器，观测负载力矩以及转动惯量，进而进行前馈补偿。