平滑滤波器（Smooth Filter）的MATLAB与Verilog仿真设计与实现

       在工程中使用PID控制器时，初期的输出结果会出现较大的波动，可能会损坏器件。为了解决这一问题，引入平滑滤波器，以有效减少波动，从而使输出结果更加平稳和稳定。

目录

1.简介

2.基本原理

3. 平滑滤波器类型

3.1 移动平均滤波器 (Moving Average Filter)

3.2 高斯滤波器 (Gaussian Filter)

4.matlab代码实现

 移动平均滤波器

高斯滤波器

5.verilog代码实现

1.简介

        平滑滤波器（Smooth Filter）可以通过去除高频噪声来减少信号的波动，使信号变得更加平滑。这种滤波器广泛应用于图像处理、声音处理、信号处理等领域。

2.基本原理

        平滑滤波器通常是通过对邻域内的数据点进行加权平均，从而消除不必要的噪声。其目的是减少信号中的高频噪声成分，同时保持信号的低频成分（即信号的基本趋势）。工作原理是将一个信号（例如时间序列、图像像素等）的每个数据点与其邻域数据点进行加权平均，进而产生一个平滑的输出信号。 所以在对于一个输入信号 x(t)，在平滑滤波器处理后，其输出信号 y(t) 可以通过以下公式表示：

• x(t) :信号在时刻 ( t ) 的原始值。
• N :滤波器窗口的大小。
• m:是窗口的一半大小（即左右各有 ( m ) 个邻近数据点参与加权平均）。

3. 平滑滤波器类型

        常见的平滑滤波器有几种类型，最常用的有移动平均滤波器 和 高斯滤波器。

3.1 移动平均滤波器 (Moving Average Filter)

        移动平均滤波器是最简单的平滑滤波器类型，它通过计算窗口内所有点的算术平均值来平滑数据。窗口大小（即采样点数）决定了滤波的程度，窗口越大，滤波效果越明显，但也会导致信号延迟。它的公式如下：

        其中 N是窗口大小， x(t) 是输入信号。

3.2 高斯滤波器 (Gaussian Filter)

        高斯滤波器是一种基于高斯分布的加权平均滤波器，它对数据点进行加权，离中心点越远的点权重越小。这种滤波器对于平滑信号、去除噪声特别有效，尤其是当噪声呈现高频波动时。
加权方式：高斯滤波器通过高斯函数计算权重，离中心点越远，权重越小，权重呈现钟形曲线。
实现原理：高斯滤波器的输出是一个基于高斯加权的平均值。其权重可以通过高斯分布公式计算：

        其中 是标准差，决定了滤波器的“宽度”。

        输出公式为：

        

        

        理论上，高斯滤波器的窗口是无限的。但在实际应用中，我们通常将和式的范围从 k=−3σ 到 k=3σ 或者根据需要设置其他窗口大小。

4.matlab代码实现

 移动平均滤波器

        由于需要在 Verilog 中实现平滑滤波器，因此我首先通过 MATLAB 来验证实现效果，从而确保 Verilog 代码的正确性。MATLAB 中自带的移动平均滤波器函数 movmean，因为我处理的是向量信号，所以使用起来非常简便。

y = movmean(A, window)

• A: 输入的数据
• window: 整数，指定滑动窗口的大小，即窗口内的元素数量。

        对应的代码：

fs = 1000;                    % 采样频率
t = 0:1/fs:1;                 % 时间向量
f = 50;                       % 信号频率
signal = 512*sin(2*pi*f*t);       % 生成正弦波信号% 添加噪声
noise = 512 * rand(size(t)) - 256; % 随机噪声(-256~256)
noisy_signal = signal + noise; % 含噪信号% 移动平均滤波器（长度为5）
window_size = 32;  % 滤波器窗口大小
smoothed_signal = movmean(noisy_signal, window_size);  % 使用movmean函数进行滤波% 原始信号
figure;
subplot(3,1,1);
plot(t, signal);
title('Original Signal');
xlabel('Time (s)');
ylabel('Amplitude');%含噪声信号（等同于输入信号）
subplot(3,1,2);
plot(t, noisy_signal);
title('Noisy Signal');
xlabel('Time (s)');
ylabel('Amplitude');%滤波后的信号
subplot(3,1,3);
plot(t, smoothed_signal);
title('Smoothed Signal (Moving Average)');
xlabel('Time (s)');
ylabel('Amplitude');

        上述代码中使用了 512sin(2*pi*f*t) 生成一个频率为 50Hz 的正弦波。然后，通过 rand 函数生成随机噪声并添加到原始信号中，形成含噪信号。再使用 MATLAB 内置的 movmean 函数实现一个窗口大小为 532的移动平均滤波器。效果如图1所示。

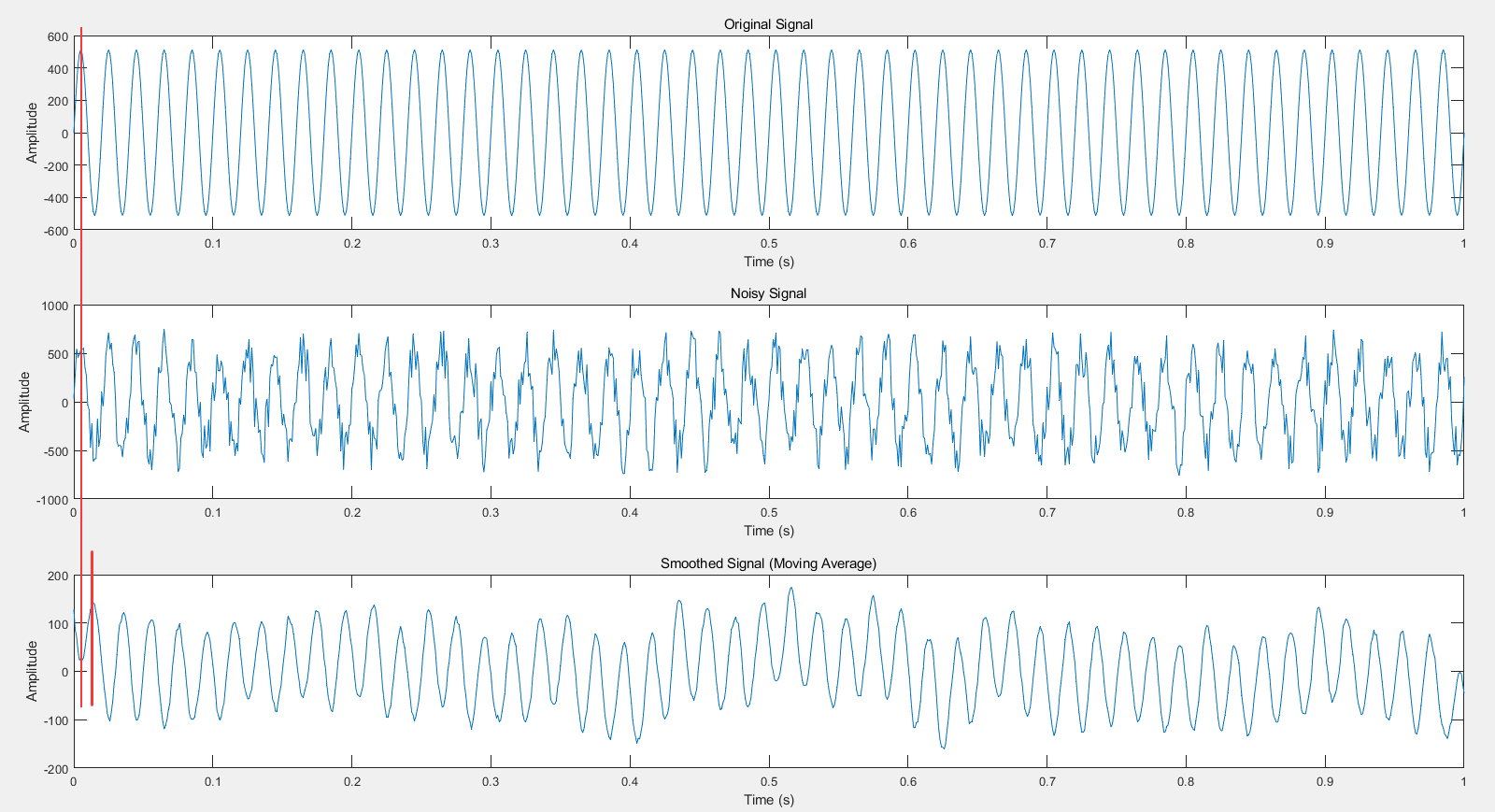
        对比含噪信号和滤波后的信号可以发现，移动平均滤波器能够有效平滑信号，去除信号中的高频噪声成分。然而，滤波后的信号强度会有所减小，并且出现信号延迟的现象。

高斯滤波器

        也是使用matlab内置的函数，用法如下：

        （1）用fspecial 函数生成高斯滤波器：

h = fspecial('gaussian', [1 11], 2)

• gaussian：指定生成一个高斯滤波器。
• [1 11]：指定滤波器的窗口大小为 1 行 11 列。这意味着生成的高斯滤波器是一个长度为 11 的一维滤波器（1x11）。
• 2：指定高斯滤波器的标准差 ，即高斯函数的宽度。标准差越大，滤波器的平滑效果越强。

        （2）filter 函数执行滤波器运算

smoothed_signal_gaussian = filter(h, 1, noisy_signal)

• h：上一步生成的高斯滤波器，它包含滤波器的权重系数。
• 1：表示滤波器的分母系数。这里的 1 代表一个简单的 FIR（有限脉冲响应）滤波器，因为高斯滤波器是一个FIR滤波器，不需要复杂的分母系数。
• noisy_signal：输入信号
• smoothed_signal_gaussian：输出结果是经过高斯滤波器平滑处理后的信号。

        对应的代码

% 生成含噪信号
fs = 1000;                   
t = 0:1/fs:1;                 
f = 50;                      
signal = 512*sin(2*pi*f*t);       
noise = 512 * rand(size(t)) - 256; % 随机噪声(-256~256)
noisy_signal = signal + noise; % 高斯滤波器
h = fspecial('gaussian', [1 11], 2);  % 高斯滤波器，窗口长度为11，标准差为2
smoothed_signal_gaussian = filter(h, 1, noisy_signal);  % 应用高斯滤波器% 原始信号
figure;
subplot(3,1,1);
plot(t, signal);
title('Original Signal');
xlabel('Time (s)');
ylabel('Amplitude');%含噪信号
subplot(3,1,2);
plot(t, noisy_signal);
title('Noisy Signal');
xlabel('Time (s)');
ylabel('Amplitude');%滤波后的信号
subplot(3,1,3);
plot(t, smoothed_signal_gaussian);
title('Smoothed Signal (Gaussian Filter)');
xlabel('Time (s)');
ylabel('Amplitude');

        生成的测试信号和移动平均滤波器一致，高斯滤波器滤波的效果如图2所示。

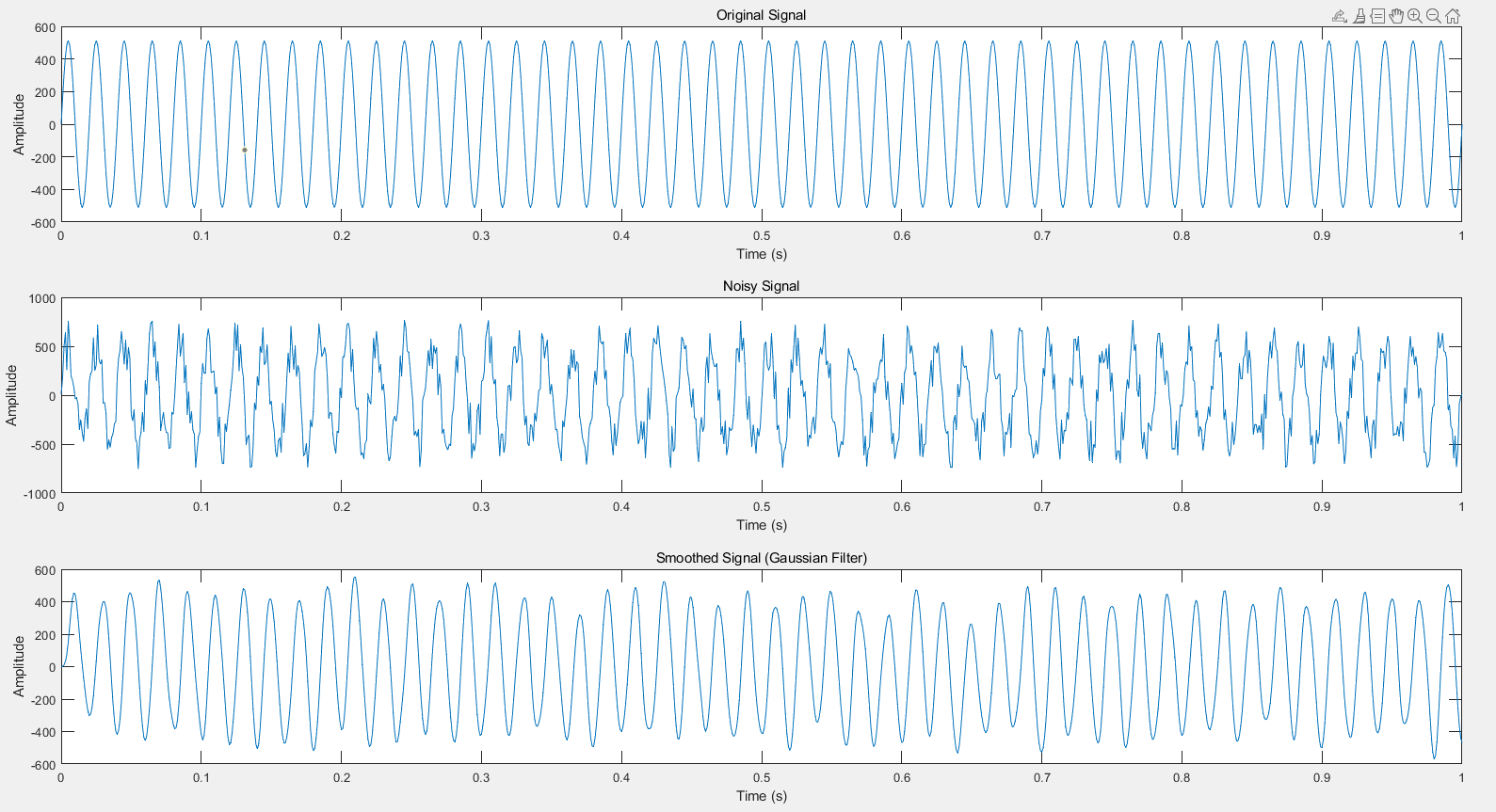
        从图2可以看出，高斯滤波器同样能够有效平滑信号，而且其引起的延迟现象相较于移动平均滤波器较轻微，整体效果优于移动平均滤波器。然而，由于高斯函数实现较为复杂，因此我不打算使用 Verilog 来实现该滤波器。

5.verilog代码实现

      由于移动平均滤波器的公式较为简单，因此实现起来也相对容易。例如，当步长为 LEN 时，可以使用 LEN 个移位寄存器来存储数据。每当新的数据输入时，将其加到 SUM 中，同时从 SUM 中减去最早输入的数据，从而保持窗口长度。待有效数据输入的数量达到 LEN 后，滤波器的输出便变得有效。

        举个例子：设输入的数据data_in是1~100，窗的长度为10。所以有10个寄存器，初值均为0，如下所示：

            因为移动平均滤波器的公式为：，所以verilog中可以写成：

sum        <= sum - shift_reg[Len-1] + data_in;

data_out    <= sum/Len;

       这样，在每个时钟周期到来时，新的数据会被加到 SUM 中，从而完成累加。当输入的数据数量达到 LEN 时，data_out 就变得有效。例如，当数据输入到第 10 个时，仍需要继续计算 SUM，此时输出尚未有效，直到下一个时钟周期才会变得有效。同时，shift_reg[LEN-1]（即 shift_reg[9]）仍为 0，因此 SUM 的计算没有问题。

       当数据输入到第 11 个时，输出数据已经变得有效。同时，shift_reg[LEN-1]（即 shift_reg[9]）为 1，此时需要从 SUM 中移除 1，以确保窗口的长度始终保持为 10。

        对应的verilog代码如下

/* * file         : smooth_filter_lhw.v* author       : yuluo_lhw* version      : v1.0* description  : 平滑（移动平均）滤波器*/
module smooth_filter_lhw#(parameter Width = 16,  // 确保这里定义了 Width 参数parameter	signed	Len		= 16'sd32	//最大取16'sd32767，不应出现负数
//这里取signed是为了使编译器正确生成有符号运算器,例如：在计算窗口总和时，sum是一个有符号的数，如果LEN被定义为无符号类型（unsigned），在与有符号数进行加减运算时可能会导致不必要的符号拓展问题。
)
(
input	wire						clk,
input	wire						rst_n,input	wire						en,
input	wire	signed	[Width-1:0]	data_in,
output	reg		signed	[Width-1:0]	data_out,output	reg							valid
);reg		signed	[Width-1:0]		shift_reg [0:Len-1];
reg		signed	[Width+15:0]	sum = 'sd0;//Shift Reg
genvar i;
generatefor(i = 0; i <= Len-1; i = i + 1) begin: SHIFT_REGalways @(posedge clk or negedge rst_n) beginif (~rst_n) beginshift_reg[i] <= 'sd0;endelse if (en) beginif (i == 0) beginshift_reg[i] <= data_in;  // 最低位赋值end else beginshift_reg[i] <= shift_reg[i-1];  // 其他位进行移位endendendend
endgenerate//sum
always @(posedge clk or negedge rst_n) beginif(~rst_n) beginsum		<= 'sd0;endelse if(en) beginsum		<= sum - shift_reg[Len-1] + data_in; //减去 shift_reg[Len-1] 是为了移除窗口中最旧的元素，确保 sum 始终是当前窗口中所有数据的和，进而可以计算出正确的滑动平均值。endelse beginsum		<= sum;end
end//data_out
always @(posedge clk or negedge rst_n) beginif(~rst_n) begindata_out	<= 'sd0;endelse begindata_out	<= sum/Len;//可以不加(cnt==Len)?，因为等valid有效之后就经过了32T，之后窗口的数据都是有效的。end
end//valid
reg		[15:0]	cnt	= 16'd0;
always @(posedge clk or negedge rst_n) begin  if(~rst_n) begincnt		<= 16'd0;endelse if(en) begincnt		<= (cnt<Len-1)? cnt+1'b1 : Len-1;endelse begincnt		<= cnt;endvalid	<= (cnt==Len-1)? 1'b1 : 1'b0;
endendmodule

verilog仿真代码：

`timescale 1ns / 1psmodule tb_smooth_filter;parameter Width = 16;
parameter Len = 32;  // 滤波器窗口大小reg clk;
reg rst_n;
reg en;
reg signed [Width-1:0] data_in;
wire signed [Width-1:0] data_out;
wire valid;// 模拟输入数据   
integer i;
reg signed [Width-1:0] signal;
reg signed [Width-1:0] noise;always begin#5 clk = ~clk;  // 10ns 时钟周期
end// 测试过程
initial beginclk = 0;rst_n = 0;en = 0;data_in = 0;signal = 0 ;noise = 0 ;#10;rst_n = 1;  #10;// 启动滤波器en = 1;//先验证计算的准确性for (i = 1; i < 50; i = i + 1) begindata_in = i; // 将信号和噪声相加#10;  // 等待一个时钟周期end//再验证滤波器的功能for (i = 0; i < 1000; i = i + 1) begin// 生成一个简单的正弦波信号，并加上噪声signal = $signed(16'd512) * $sin(2 * 3.141592 * i / 50); // 简单正弦波:T = 2Snoise = $signed($random % 256); // 生成噪声(均匀分布)data_in = signal + noise; // 将信号和噪声相加#10;  // 等待一个时钟周期end#100;$finish;
end// 显示输出
initial begin$monitor("Time: %t | data_in: %d | data_out: %d | valid: %b", $time, data_in, data_out, valid);
endsmooth_filter_lhw #(.Width(Width),.Len(Len)
) uut (.clk(clk),.rst_n(rst_n),.en(en),.data_in(data_in),.data_out(data_out),.valid(valid)
);endmodule

        仿真的输入波形和matlab的类似。需要说明的是，在仿真代码中可以直接使用sin,randm这些函数，但是在硬件设计中，这些函数并不能直接用于实现。

仿真波形如下：

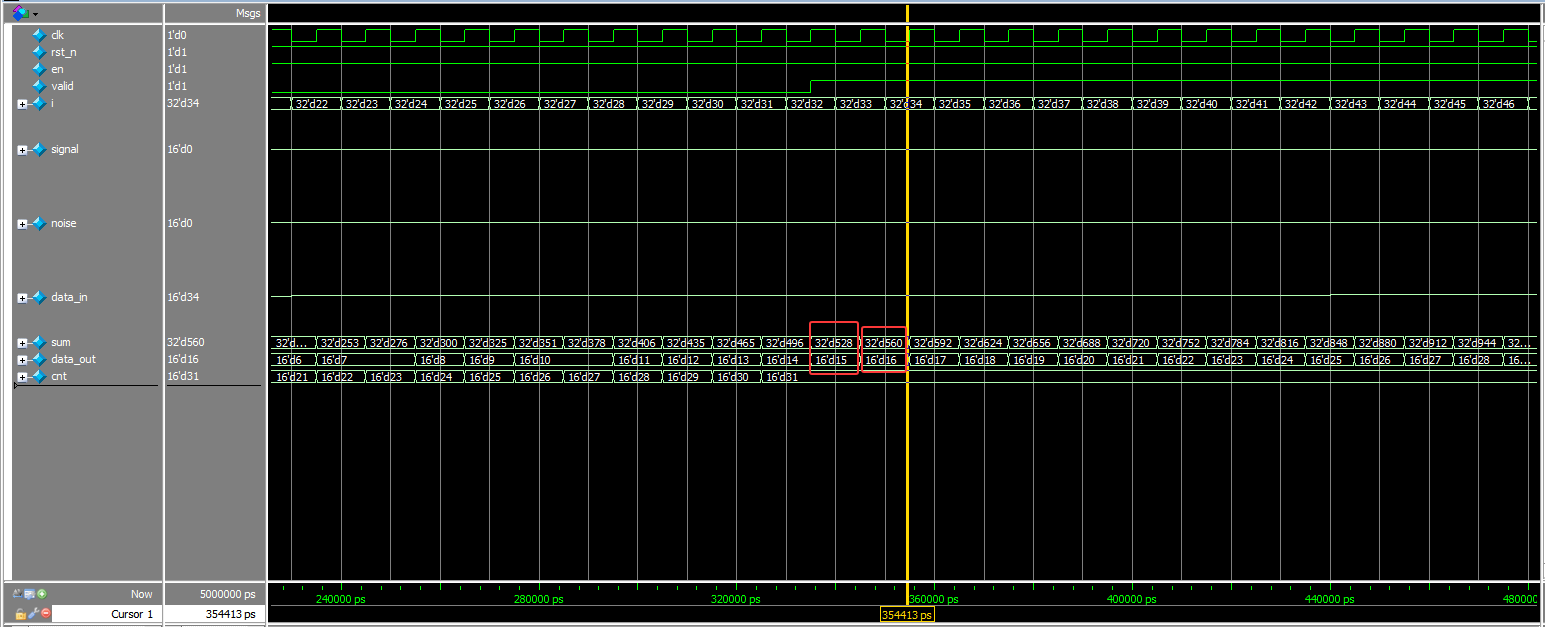
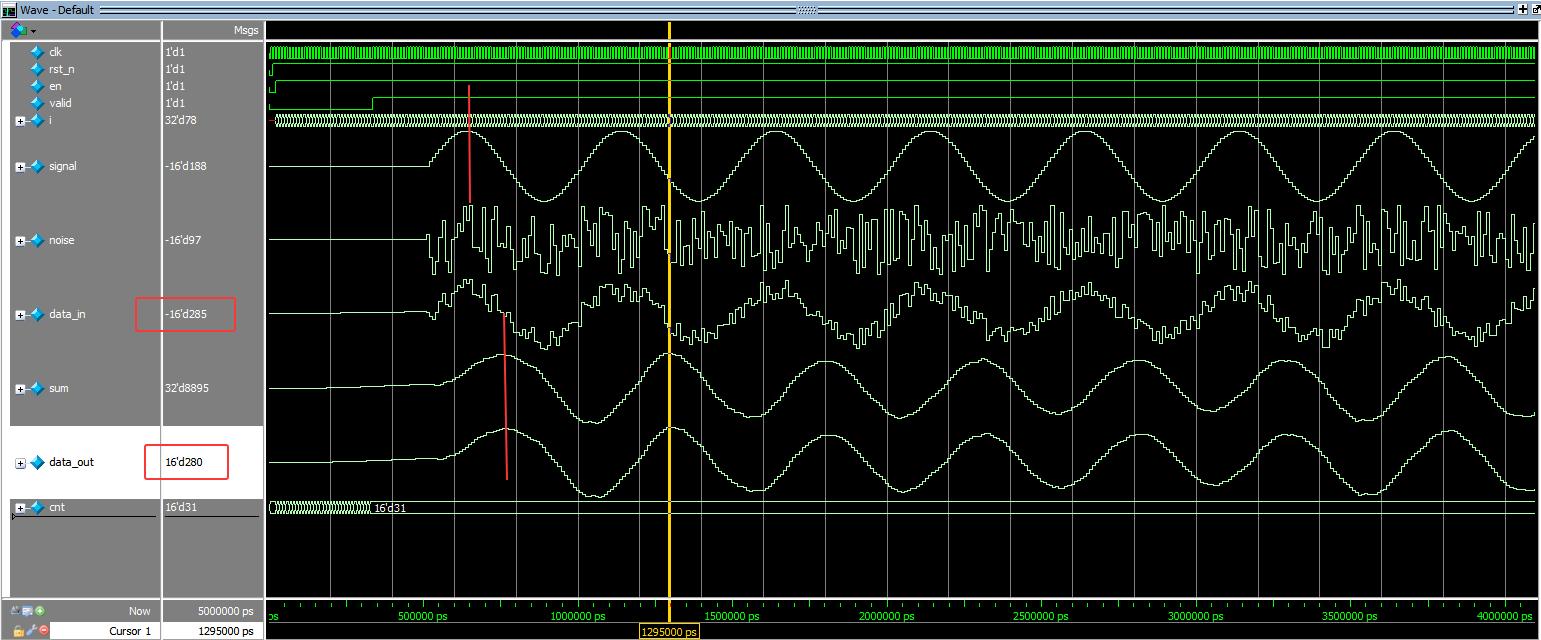
        从图7可以看出，设计中的滤波器公式计算是正确的。当数据有效时，输出结果正好是 1 到 32 的累加和，等于 528。图8展示了该设计具备了移动平均滤波器的平滑功能，但也伴随了一定的延迟。这一点的解释也变得非常直观：刚开始时，数据尚未进入滤波器，因此窗口内的数据为 0，经过除以窗口长度（LEN）后，输出会是一个非常小的值，接近于零，或者不具有代表性。这就产生了初期的延迟。这就是为什么在初期会出现延迟的原因。

        以上就是本次分享，欢迎大家加我为好友（QQ：235840795），一起交流与学习！