PySINDy

PySINDy
A Python package for the Sparse Identification of Nonlinear Dynamics from Data

Abstract

PySINDy 是一个用于从数据中发现主导动力系统模型的 Python 软件包。具体来说，PySINDy 提供了应用非线性动力学稀疏辨识（SINDy）[1] 方法进行模型发现的工具。本文简要描述了 SINDy 的数学基础，概述并演示了 PySINDy 中实现的功能（附代码示例），提供了给用户的实用建议，以及PySINDy 的潜在扩展功能列表。

软件可在 https://github.com/dynamicslab/pysindy 获取。

[1]  S. L. Brunton, J. L. Proctor, and J. N. Kutz, “Discovering governing equations from data by sparse identification of nonlinear dynamical systems,” Proceedings of the National Academy of Sciences, vol. 113, no. 15, pp. 3932–3937, 2016.

1 引言

长期以来，科学家们通过建立数学模型来量化实证观测结果，这些模型能够刻画观测现象、具备一定的可解释性并能进行预测。尤其是动力学系统模型已被广泛应用于研究、解释和预测众多应用领域中的行为，其范例涵盖从牛顿经典力学定律到用于模拟酶动力学的米氏动力学方程。虽然控制定律和方程传统上是从第一性原理和专家知识推导得出，但当前可用测量数据的增长以及由此产生的对数据驱动建模的重视，推动了自动化模型发现的算法化与可复现方法的发展。

近年来已开发出许多此类方法[2]，包括线性方法[3, 4]、动态模式分解（DMD）[5, 6]及更广义的Koopman理论[7–12]、非线性自回归算法[13, 14]、神经网络[15–24]、高斯过程回归[25, 26]、算子辨识与降阶建模[27–29]、非线性拉普拉斯谱分析[30]、扩散映射[31]、遗传编程[32–34]以及稀疏回归[1, 35]。要最大化这些模型发现方法的影响力，就需要开发工具使其能够被不同领域、具有不同数学专业水平的科学家广泛使用。

PySINDy 是一个用于从数据中发现控制动力学系统模型的 Python 软件包。具体来说，PySINDy 提供了应用非线性动力学稀疏辨识（SINDy） 方法进行模型发现的工具。SINDy 将模型发现问题构建为一个稀疏回归问题，即从候选函数库中筛选出动力学中的相关项，这些候选函数的选取很大程度上源于我们对各种物理模型的深厚历史知识。这种方法产生了可解释的模型，并已被广泛应用和拓展[35, 37, 51–63]，采用了不同的稀疏优化算法和库函数。

PySINDy 软件包面向研究人员和实践者，旨在让任何能够获取测量数据的人都能够参与科学模型发现。该软件包遵循 scikit-learn 标准，设计得对经验不足的用户易于使用，同时也为高级用户提供了可定制的选项。软件包实现了许多流行的 SINDy 变体，但其设计也支持为了研究和实验而进行进一步的扩展。

2 背景

PySINDy 提供了 SINDy 方法的实现，用于发现如下形式的控制动力学系统模型：

给定形式为状态测量值  的数据，SINDy 辨识出一个描述系统状态随时间演化的动力学模型，即函数 f。具体而言，SINDy 在一个候选基函数库  中对动力学进行稀疏逼近，使得：

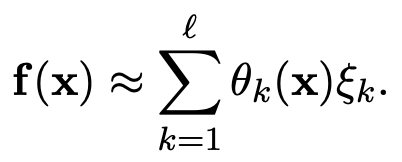
其中大多数系数 ξk 为零，非零项标识了动力学中的活跃项。为了将 SINDy 构建为一个回归问题，将 x 的时间序列测量值及其时间导数  排列成矩阵：

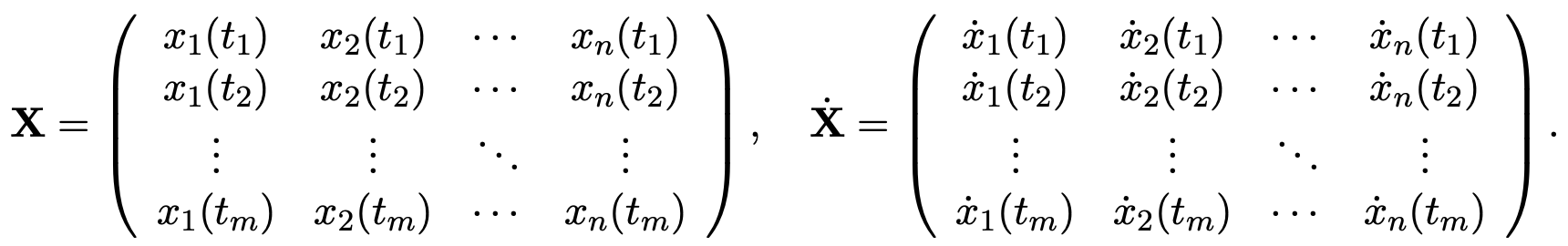
导数可以通过数值方法近似或直接测量得到。随后在数据上评估这些库函数，得到 。接着执行稀疏回归以近似求解：

其中  是一组决定 f 中活跃项的系数。虽然最初的 SINDy 公式使用顺序阈值最小二乘算法（STLSQ）[1, 64] 求解 (2)，但该问题可以使用任何稀疏回归算法来解决，例如套索算法（Lasso）[65]、稀疏松弛正则化回归（SR3）[66, 67]、逐步稀疏回归（SSR）[58] 或贝叶斯方法[68–70]。

SINDy 已被广泛应用于模型辨识，应用领域包括化学反应动力学[40]、非线性光学[36]、流体动力学[37, 39, 41, 42, 47] 和湍流建模[48, 50]、等离子体对流[38]、数值算法[45] 以及结构建模[46] 等[43, 44, 49]。它也被扩展以处理更复杂的建模场景，例如偏微分方程[35, 52]、具有输入或控制的系统[59]、具有隐式动力学的系统[51]、混合系统[60]、强制执行物理约束[37]、结合信息论[53]、从损坏或有限数据[54, 56] 以及初始条件集合[57] 中识别模型，并将公式扩展至包含积分项[55, 63]、张量表示[61, 62] 和随机强迫[58]。然而，目前并没有一个确定的标准实现或软件包用于 SINDy。SINDy 的版本已在更大的项目（如 sparsereg[71]）中实现，但没有一个特定的实现成为最广泛采用的版本，并且大多数版本只实现了有限的功能集。因此，研究人员通常需要编写自己的实现，这导致了重复劳动和缺乏标准化。这不仅使得将 SINDy 应用于科学数据集更加困难，而且使得对该方法的扩展进行基准测试更具挑战性，并使最终用户更难以获取这些扩展。这促使本文创建一个专用于 SINDy 的软件包。PySINDy 软件包提供了一个核心代码库，其中实现了许多基本的 SINDy 功能，便于使用和标准化。此外，用户可以轻松地扩展 PySINDy，从而使更广泛的研究社区能够获取新的开发成果。

3 特性

PySINDy 软件包中的核心对象是 SINDy 模型类，它被实现为一个 scikit-learn 估计器。做出这一设计选择是为了确保该软件包对广大用户群体来说简单易用，因为许多潜在用户都熟悉 scikit-learn。它还在适当的抽象层级上表达了 SINDy 模型对象，以便用户可以将其嵌入到 scikit-learn 中更复杂的管道中，例如用于参数调整和模型选择。

PySINDy 实现涉及三个主要步骤，对应着三个建模决策：

1. 用于从 X 近似 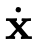 的数值微分方案；

2. 构成特征库 Θ 的候选函数；

3. 应用于求解 (2) 以找到 Ξ 的稀疏回归算法。

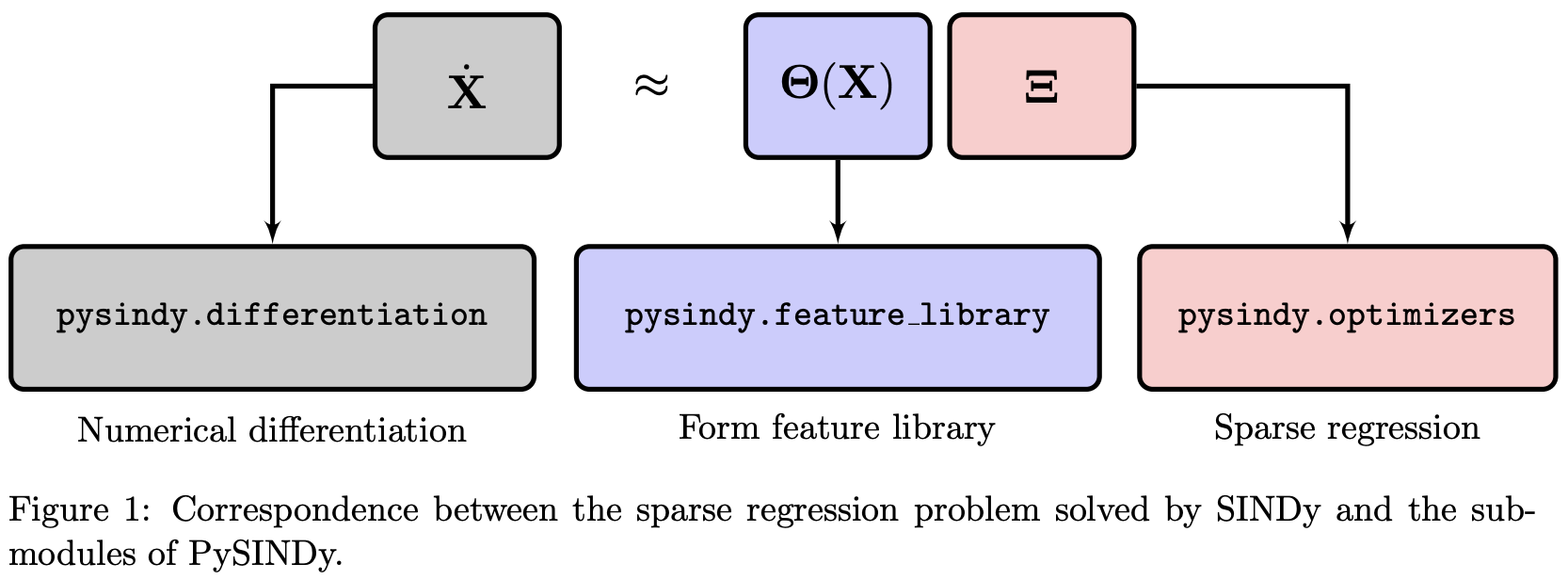
核心 SINDy 对象的设计旨在以尽可能模块化的方式整合这三个组件，每个组件对应一个属性：用于数值微分的 SINDy.differentiation_method，用于构建候选函数库的 SINDy.feature_library，以及用于稀疏回归器的 SINDy.optimizer。PySINDy 为每个步骤提供了标准选项，同时可以轻松地用更复杂的“第三方”算法替换任何步骤。本文实现了以下方法：

• 数值微分 (用于从 X 计算 )

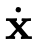  • 有限差分: FiniteDifference

  • 平滑有限差分: SmoothedFiniteDifference

• 特征库 (用于构建 Θ)

  • 多元多项式: PolynomialLibrary

  • 傅里叶模式 (即三角函数): FourierLibrary

  • 自定义库 (由用户提供的函数定义): CustomLibrary

  • 恒等库 (用于用户希望自行计算 Θ 的情况): IdentityLibrary

• 优化器 (用于执行稀疏回归)

  • 顺序阈值最小二乘法[1, 64]: STLSQ

  • 稀疏松弛正则化回归 (SR3)[66]: SR3

4 示例

PySINDy 的 GitHub 页面1包含了以 Jupyter notebooks 形式提供的教程。这些教程演示了该软件包各种功能的使用方法，并复现了原始 SINDy 论文 [1] 中的示例。本节将使用洛伦兹方程 (3) 作为动力系统来演示 PySINDy 软件包：

在 Python 中，(3) 的右手边可以表示如下：

def lorenz ( x , t ) :return [10 ∗ ( x [ 1 ] - x [ 0 ] ) ,x [ 0 ] ∗ ( 2 8 - x [ 2 ] ) - x [ 1 ] ,x [ 0 ] ∗ x [ 1 ] - ( 8 / 3 ) ∗ x [ 2 ]
]

为了构建输入 SINDy 模型的训练数据，使用以下代码对 (3) 进行积分：

import numpy as np
from scipy . integrate import odeint
dt = 0. 0 0 2
t = np . arange ( 0 , 1 0 , dt )
x0 = [ - 8 , 8 , 2 7]
X = odeint ( lorenz , x0 , t )

在图 2 中绘制了 X。重要的是要注意，X 的每一列对应一个变量，每一行对应一个时间点。所有处理数据的 PySINDy 对象都假定数据是按这种方式构建的。

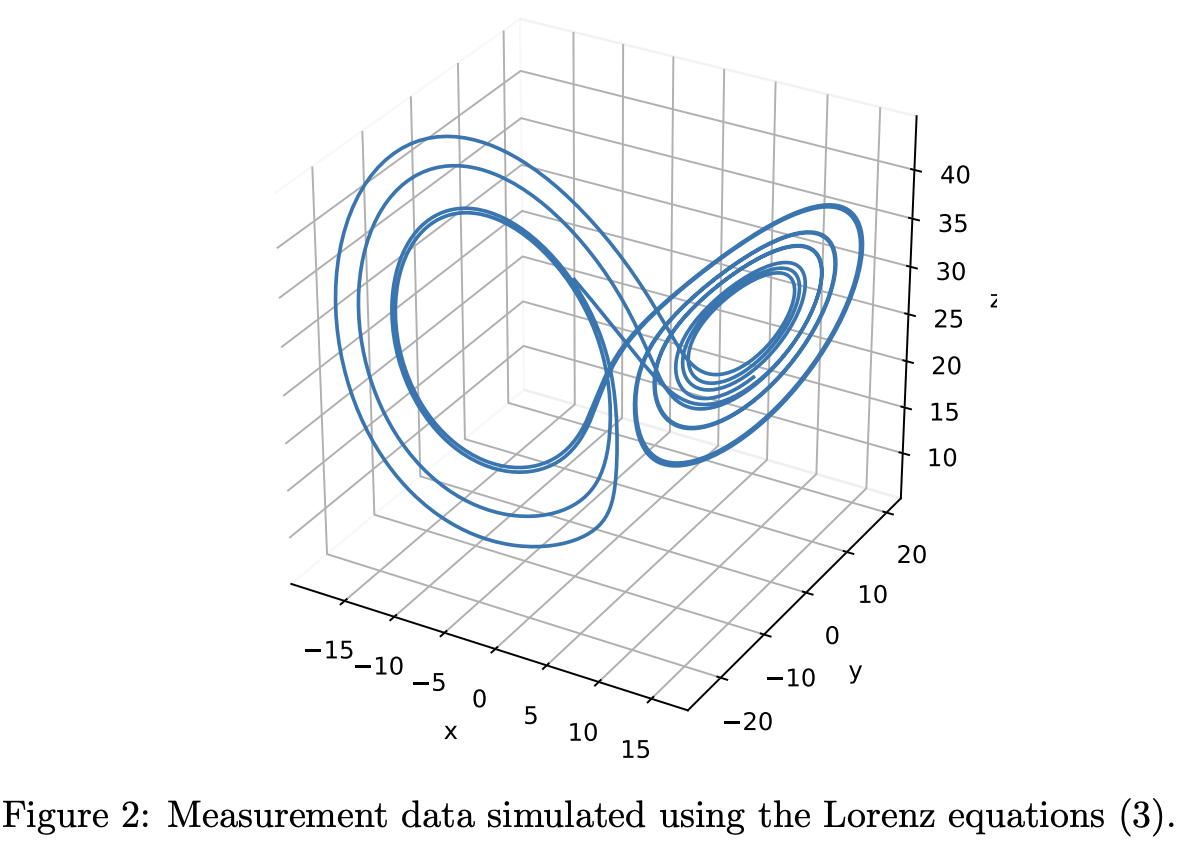
4.1 基本用法

pysindy 软件包围绕 SINDy 类构建，该类封装了使用 SINDy 学习动力系统所需的所有步骤。要创建一个 SINDy 对象，将其与数据拟合（即从数据中推断出一个动力系统），并打印得到的模型，需要调用 SINDy 的构造函数、fit 方法和自定义的打印函数：

model = ps . SINDy ( )
model . fit ( X , t=dt )
model . print ( )

其输出为：

x0’ = -9.999 x0 + 9.999 x1
x1’ = 27.992 x0 + -0.999 x1 + -1.000 x0 x2
x2’ = -2.666 x2 + 1.000 x0 x1

一旦 SINDy 对象完成拟合，就可以输入新数据，并使用学习到的模型来预测每次测量的导数（请记住，测量值对应于行）。

t_test = np . arange ( 0 , 1 5 , dt )
x0_test = np . array ( [ 8 , 7 , 1 5 ] )
X_test = odeint ( lorenz , x0_test , t_test )
X_dot_test_computed = model . differentiate ( X_test , t=dt )
X_dot_test_predicted = model . predict ( X_test )

调用 model.differentiate(X_test, t=dt) 会将 SINDy 模型中的数值微分方法应用于 X_test，时间步长为 dt。

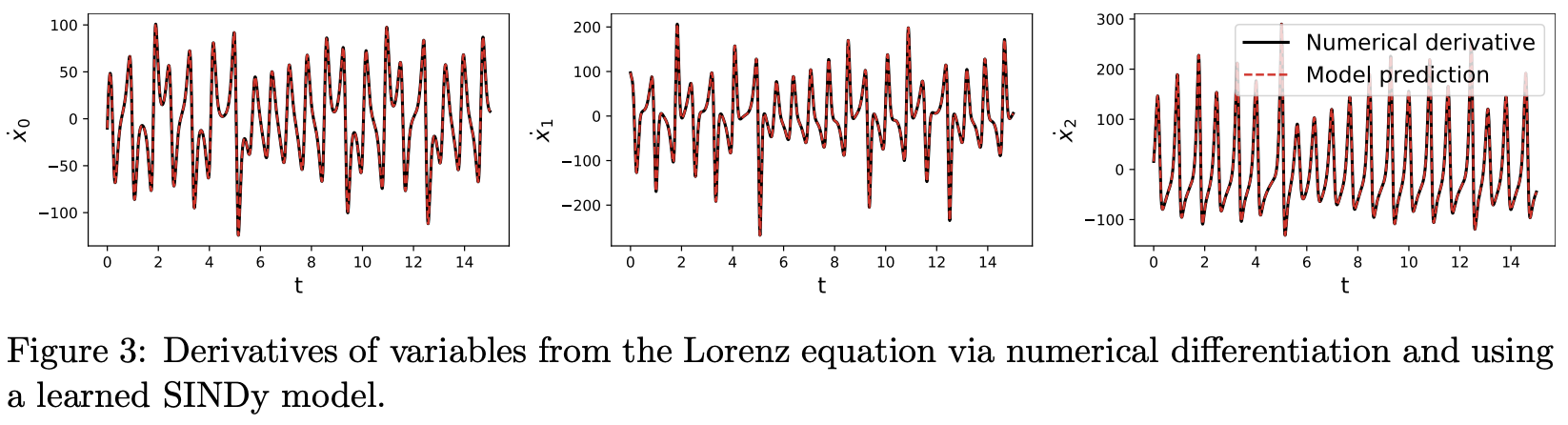
图 3 绘制了计算得到的 X_dot_test 和预测得到的 X_dot_test 的每个维度。与预测导数相比，通常更感兴趣的是使用学习到的模型将初始条件随时间向前演化（即模拟仿真）。simulate 函数正是做这个的。

X_test_sim = model . simulate ( x0_test , t_test )

图 4 显示了根据学习模型模拟的轨迹与真实轨迹 X_test 的对比图。轨迹在初始阶段一致，但由于洛伦兹方程的混沌特性，它们最终会分岔。

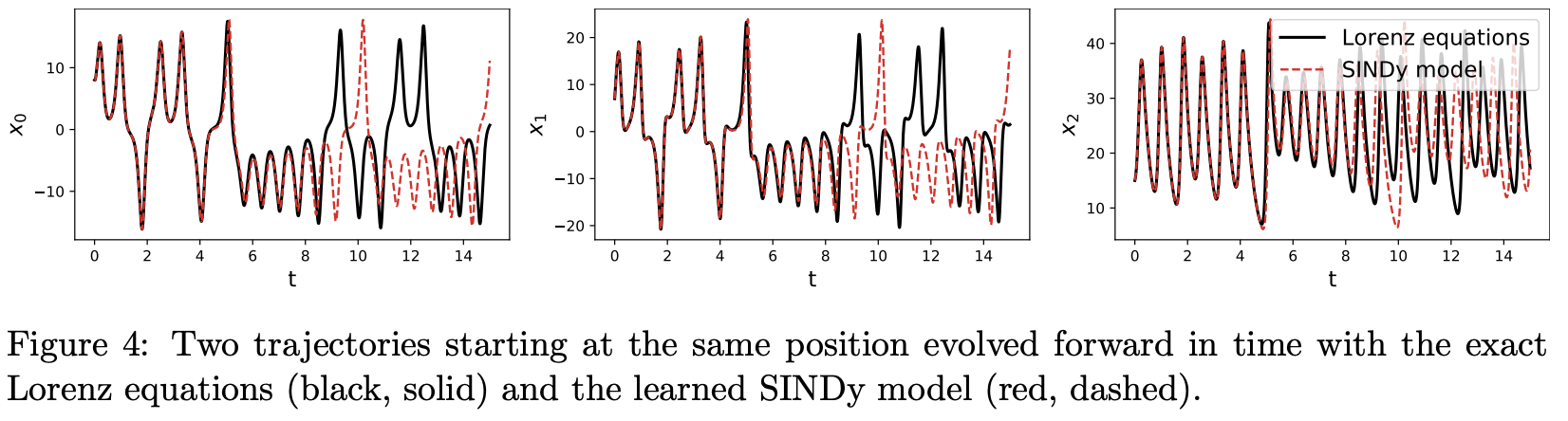
4.2 自定义特性

本文依赖 SINDy 对象的默认选项，但 PySINDy 配备了多种可替代的内置方法用于微分、库构建和优化。这些选项通过分别向 SINDy 构造函数的 differentiation_method、feature_library 和 optimizer 参数传递相应的 PySINDy 对象来选择。微分、库和优化算法的参数是提供给相应对象的构造函数，而不是直接提供给 SINDy 对象。本文通过以下示例演示语法：

differentiation_method = ps . FiniteDifference ( order=1 )
feature_library = ps . PolynomialLibrary ( degree=3 , include_bias=False )
optimizer = ps . SR3 ( threshold=0 . 1 , nu=1 , tol=1e - 6 )
model = ps . SINDy (differentiation_method=differentiation_method ,feature_library=feature_library ,optimizer=optimizer ,feature_names=[ "x" , "y" , "z" ]
)
model . fit ( X , t=dt )
model . print ( )

这将打印出：

x’ = -10.021 x + 9.993 y
y’ = 28.431 x + -1.212 y + -1.008 x z
z’ = -2.675 z + 1.000 x y

还有许多其他内置选项可用。

The official documentation 2 and examples 3 provide an exhaustive list.

2 https://pysindy.readthedocs.io/en/latest/index.html

3 https://github.com/dynamicslab/pysindy/tree/master/example

5 实用建议

本节提供有效使用 PySINDy 的实用性建议。本文将讨论潜在的陷阱及应对策略。在适用的情况下，本文还会说明如何整合 PySINDy 未原生实现的自定义方法。此处提供的信息结合了实践经验和理论考量。

5.1 数值微分

数值微分是 SINDy 方法的核心组件之一。测量变量的导数提供了稀疏回归问题 (2) 的目标值。如果在计算这些导数时不够谨慎，学习到的模型质量很可能会受到影响。

默认情况下，使用二阶有限差分法来对输入数据进行微分。有限差分法往往会放大数据中的噪声。如果数据是光滑的（至少二阶可微），那么有限差分法能给出精确的导数近似值。而当数据含有噪声时，它们给出的导数估计值会比原始数据含有更多的噪声。图 5 可视化了噪声对数值导数的影响。请注意，即使是数据中少量的噪声，也会导致数值导数的质量显著下降。

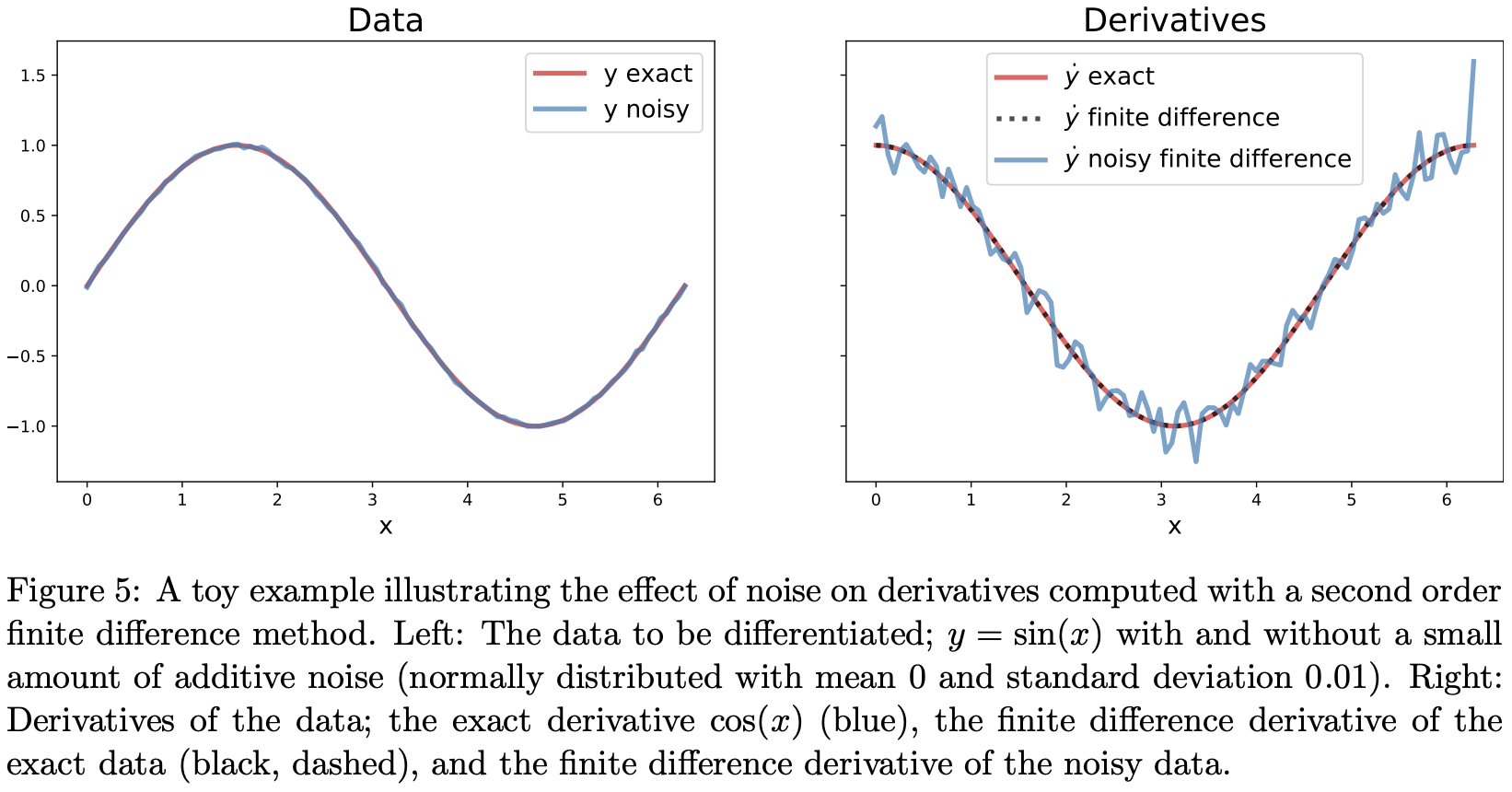
减轻噪声影响的一种方法是在计算导数之前平滑测量值。SmoothedFiniteDifference 方法可用于此目的。也有人提出了采用全变差正则化的数值微分方案 [72]，并推荐在 SINDy 中使用 [1]。

希望使用自己数值微分方案的用户有两种方法可以实现。输入测量值的导数可以在外部使用所选方法计算，然后通过 x_dot 关键字参数直接传递给 SINDy.fit 方法。或者，用户可以实现自己的微分方法，并通过 differentiation_method 参数将其传递给 SINDy 构造函数。在这种情况下，提供的类只需实现一个接受两个参数 x 和 t 的 __call__ 方法即可。

5.2 库选择

SINDy 方法假设动力学可以表示为库函数的稀疏线性组合。如果这个假设不成立，该方法的性能很可能表现不佳。这个问题通常表现为大量库项被激活（即系数非零），且这些项的权重量级差异巨大，但最终仍导致较大的模型误差。

通常，应利用对所研究系统及其动力学的先验知识来明智地选择基函数。当此类信息不可用时，默认的库函数类——多项式——是一个很好的起点，因为光滑函数具有快速收敛的泰勒级数。Brunton 等人 [1] 表明，配备多项式库的 SINDy 可以恢复真实右手边函数 f(x) （在零点处的）泰勒级数的前几项。如果有理由相信动力学可以用切比雪夫多项式而非单项式进行稀疏表示，那么库中就应该包含切比雪夫多项式。

PySINDy 包含 CustomLibrary 和 IdentityLibrary 对象，以提供库函数方面的灵活性。当所需的库由一组需要依次应用于每个测量变量（或变量对、三元组等）的函数组成时，应使用 CustomLibrary 类。IdentityLibrary 类的可定制性最强，但将计算库函数的工作转移给了用户。它期望用户希望包含在库中的所有特征都已被计算好并在调用 SINDy.fit 之前就已存在于 X 中，因为它只是对传递给它的每个变量应用恒等映射。它最适用于那些对如何应用库函数有非常具体要求的情况（例如，某些函数只应应用于某些输入变量）。

随着项被添加到库中，底层的稀疏回归问题会变得越来越病态。因此，建议从一个小的库开始，然后逐渐扩大其规模，直到达到所需的性能水平。例如，用户可能希望从一个线性项库开始，然后根据需要添加二次项和三次项以提高模型性能。为了获得最佳结果，应按比例增加所应用正则化的强度，以应对由此产生的线性系统日益恶化的条件数。

用户也可以选择实现针对其应用定制的库类。要做到这一点，新类应该继承自本文的BaseFeatureLibrary 类。有关新类需要实现哪些功能的指导，请参阅文档。

5.3 优化

PySINDy 使用各种优化器来解决稀疏回归问题。对于一个固定的微分方法、输入集和候选库，SINDy 识别出的动力系统仍然存在一些差异，这取决于所使用的优化器。

PySINDy 中的默认优化器是顺序阈值最小二乘算法 (STLSQ)。它不仅是最初为 SINDy 提出的方法，而且涉及单个、易于解释的超参数，并在各种问题上表现出良好的性能。

当 STLSQ 的结果不令人满意时，可以使用稀疏松弛正则化回归 (SR3) [66, 67] 算法。它涉及更多可以调整的超参数以提高准确性。特别是，thresholder 参数控制所应用的正则化类型。为了获得最佳结果，尝试使用 L0、L1 和剪切绝对偏差 (CAD) 正则化可能会有所帮助。其他超参数可以通过交叉验证进行调整。

也支持自定义或第三方稀疏回归方法。只需实例化一个自定义对象，并使用 optimizer 关键字将其传递给 SINDy 构造函数。本文的实现与 Scikit-learn 中的任何线性模型（例如 RidgeRegression、Lasso 和 ElasticNet）兼容。有关自定义优化器需要实现的方法和属性的列表，请参阅文档。在那里您还可以找到一个使用 Scikit-learn 的 Lasso 对象执行稀疏回归的示例。

5.4 正则化

正则化，在此上下文中，是一种用于改善病态问题条件的技术。如果不使用正则化，通常会得到高度不稳定的结果，学习到的参数值对于略微不同的输入会存在显著差异。SINDy 寻求那些能将动力学表示为库函数稀疏线性组合的权重。当测量数据或库的列存在统计相关性时（对于大型库很可能发生），SINDy 逆问题会迅速变为病态。尽管稀疏约束本身也是一种正则化，但对于许多问题，需要另一种形式的正则化才能使 SINDy 学习到鲁棒的动力系统模型。

在某些情况下，正则化可以解释为对模型参数强制执行先验分布[73]。应用强正则化会使学习到的权重偏离能够最好地拟合数据的值，而偏向先验分布偏好的值（例如，L2 正则化对应于高斯先验）。因此，一旦发现了一组稀疏的非零系数，本文的方法会应用一个额外的“去偏”步骤，在该步骤中使用无正则化的最小二乘法来找出已识别的非零系数的值。本文所有内置方法默认都使用正则化。

以下是一些关于正则化的通用最佳实践。大多数问题都会从一定量的正则化中受益。随着候选右手边库规模的增大，应增加正则化强度。如果在调用 SINDy.fit 时生成了关于病态矩阵的警告，更多的正则化可能会有所帮助。本文还建议在调用 SINDy.fit 方法时将 unbias 参数设置为 True，尤其是在应用大量正则化时。可以使用交叉验证来为给定问题选择适当的正则化参数。

6 扩展

在本节中，本文列出了对 SINDy 实现的潜在扩展和增强。本文为那些受先前研究启发的改进提供了参考文献，并说明了其他潜在更改的基本原理。

• 偏微分方程 (PDEs)：虽然由常微分方程 (ODEs) 给出的动力系统为物理系统建模提供了一种灵活的方法，但许多系统本质上是由偏微分方程 (PDEs) 描述的，而使用 PySINDy 无法直接发现这些方程。作为 SINDy 方法的扩展，已经提出了多种数据驱动发现 PDE 的方法 [35, 52]，这些方法可以很容易地纳入 PySINDy 框架中。

• 识别坐标和潜变量：许多复杂系统（例如流体流动）是高维的，但又表现出可用于建模的低维模式[74–76]。识别用于构建模型的有效坐标系是数据驱动发现的一个重要方面。最近，SINDy 已被嵌入到自编码器框架中 [23]，以同时识别有效坐标和稀疏动力学。类似地，对于许多系统，无法测量系统的完整状态，因此存在潜变量。时间延迟坐标对于从有限测量中识别稀疏模型非常有用 [12]。这两者都是未来扩展的候选方向。

• 约束条件：SINDy 已被扩展以在稀疏回归步骤中强制执行物理约束[37]。当处理具有已知守恒量（例如不可压缩流体中的能量守恒 [37]）的物理系统时，这种方法可以将此先验信息自动纳入模型发现过程。

• 积分形式：本文之前讨论了噪声过多的测量数据如何干扰模型发现过程，并提出了平滑作为一种可能的解决方案。另一种方法是使用 (1) 的积分形式，如 Schaeffer 和 McCalla [55] 所提出，并被 Reinbold, Gurevich, 和 Grigoriev [63] 扩展到 PDE。数值微分往往会放大噪声，而数值积分往往会平滑噪声。这种形式已被证明可以提高 SINDy 对噪声的鲁棒性。

• 集成方法：集成方法是机器学习中一类经过验证的方法，旨在以额外计算为代价来减少方差（提高模型泛化能力）。它不是训练单个模型，而是训练多个高方差模型并将它们的预测结果进行平均。本文认为集成学习的思想可以加以调整，以提高 SINDy 模型的性能。最近的工作已经暗示了可能的方法 [77]。

• 扩展库：选择合适的基来表示动力学对于 SINDy 的成功应用至关重要。虽然本文目前提供的方法允许用户灵活地输入自己的库函数，但本文旨在通过提供一套通用的用于创建和组合候选函数集的工具来使库的构建过程更加容易。可以原生支持更多的基函数，例如非自治项（那些显式依赖于因变量——时间——的项）。更进一步，用户可以指定不应出现在 (2) 式左侧的特定变量（X 的列）。这将使 SINDy 能够包含输入和控制变量[59]。还可以实现作用于一个或多个库的操作。例如，通过并集、交集、组合或张量积来组合库，可以支持表达复杂的非线性动力学。能够将库仅应用于状态变量的子集，有助于降低计算成本并改善 SINDy 内求解的稀疏回归问题的条件。

[3] Nonlinear system identification: from classical approaches to neural networks and fuzzy models. Springer, 2013.
[4] Perspectives on system identification, Annual Reviews in Control, 2010.

[5] Dynamic mode decomposition of numerical and experimental data, Journal of fluid mechanics, 2010.
[6] Dynamic Mode Decomposition: DataDriven Modeling of Complex Systems. SIAM, 2016.

[7] Applied Koopmanism a), Chaos: An Interdisciplinary Journal of Nonlinear Science, 2012.
[8] Analysis of fluid flows via spectral properties of the Koopman operator, Annual Review of Fluid Mechanics, 2013.
[9] A data-driven approximation of the Koopman operator: extending dynamic mode decomposition, Journal of Nonlinear Science, 2015.
[10] Data-driven model reduction and transfer operator approximation, Journal of Nonlinear Science, 2018.
[11] Extended dynamic mode decomposition with dictionary learning: A data-driven adaptive spectral decomposition of the koopman operator, Chaos: An Interdisciplinary Journal of Nonlinear Science, 2017.
[12] Chaos as an intermittently forced linear system, Nature Communications, 2017.

[13] Fitting autoregressive models for prediction, Ann Inst Stat Math, 1969.
[14] Nonlinear system identification: NARMAX methods in the time, frequency, and spatiotemporal domains. John Wiley & Sons, 2013.

[15] Pde-net: Learning pdes from data, arXiv preprint arXiv:1710.09668, 2017.
[16] Physics-informed generative adversarial networks for stochastic differential equations, arXiv preprint arXiv:1811.02033, 2018.
[17] Time-lagged autoencoders: Deep learning of slow collective variables for molecular kinetics, The Journal of Chemical Physics, 2018.
[18] VAMPnets: Deep learning of molecular kinetics, Nature Communications, 2018.
[19] Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks, Proc. R. Soc. A, 2018.
[20] Model-free prediction of large spatiotemporally chaotic systems from data: a reservoir computing approach, Physical review letters, 2018.
[21] Deepxde: A deep learning library for solving differential equations, arXiv preprint arXiv:1907.04502, 2019.
[22] Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, Journal of Computational Physics, 2019.
[23] Data-driven discovery of coordinates and governing equations, Proceedings of the National Academy of Sciences, 2019.
[24] Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations,” Science, 2020.

[25] Machine learning of linear differential equations using gaussian processes, arXiv preprint arXiv:1701.02440, 2017.
[26] Hidden physics models: Machine learning of nonlinear partial differential equations, Journal of Computational Physics, 2018.

[27] A survey of projection-based model reduction methods for parametric dynamical systems, SIAM review, 2015.
[28] Data-driven operator inference for nonintrusive projection-based model reduction, Computer Methods in Applied Mechanics and Engineering, 2016.
[29] Lift & learn: Physics-informed machine learning for large-scale nonlinear dynamical systems, Physica D: Nonlinear Phenomena, 2020.

[30] Nonlinear laplacian spectral analysis for time series with intermittency and low-frequency variability, Proceedings of the National Academy of Sciences, 2012.

[31] Reconstruction of normal forms by learning informed observation geometries from data,” Proceedings of the National Academy of Sciences, 2017.

[32] Automated reverse engineering of nonlinear dynamical systems, Proceedings of the National Academy of Sciences, 2007.
[33] Distilling free-form natural laws from experimental data, Science, 2009.
[34] Automated adaptive inference of phenomenological dynamical models, Nature communications, 2015.

[35] Data-driven discovery of partial differential equations, Science Advances, 2017.

[37] Constrained sparse Galerkin regression, Journal of Fluid Mechanics, 2018.

[51] Inferring biological networks by sparse identification of nonlinear dynamics, IEEE Transactions on Molecular, Biological, and Multi-Scale Communications, 2016.
[52] Learning partial differential equations via data discovery and sparse optimization, in Proc. R. Soc. A, 2017.
[53] Model selection for dynamical systems via sparse regression and information criteria, Proceedings of the Royal Society A, 2017.
[54] Exact recovery of chaotic systems from highly corrupted data,” Multiscale Modeling & Simulation, 2017.
[55] Sparse model selection via integral terms, Physical Review E, 2017.
[56] Extracting sparse high-dimensional dynamics from limited data, SIAM Journal on Applied Mathematics, 2018.
[57] Numerical aspects for approximating governing equations using data, arXiv preprint arXiv:1809.09170, 2018.
[58] Sparse learning of stochastic dynamical equations, The Journal of chemical physics, 2018.
[59] Sparse identification of nonlinear dynamics for model predictive control in the low-data limit, Proceedings of the Royal Society of London A, 2018.
[60] Model selection for hybrid dynamical systems via sparse regression, Proceedings of the Royal Society A, 2019.
[61] Multidimensional approximation of nonlinear dynamical systems, Journal of Computational and Nonlinear Dynamics, 2019.
[62] Tensor network approaches for learning non-linear dynamical laws, arXiv preprint arXiv:2002.12388, 2020.
[63] Using noisy or incomplete data to discover models of spatiotemporal dynamics, Physical Review E, 2020.

[64] L. Zhang and H. Schaeffer, “On the convergence of the sindy algorithm,” Multiscale Modeling & Simulation, vol. 17, no. 3, pp. 948–972, 2019. [65] R. Tibshirani, “Regression shrinkage and selection via the lasso,” Journal of the Royal Statistical Society. Series B (Methodological), vol. 58, no. 1, pp. 267–288, 1996. [Online]. Available: http://www.jstor.org/stable/2346178 [66] P. Zheng, T. Askham, S. L. Brunton, J. N. Kutz, and A. Y. Aravkin, “A unified framework for sparse relaxed regularized regression: Sr3,” IEEE Access, vol. 7, pp. 1404–1423, 2018. [67] K. Champion, P. Zheng, A. Y. Aravkin, S. L. Brunton, and J. N. Kutz, “A unified sparse optimization framework to learn parsimonious physics-informed models from data,” arXiv preprint arXiv:1906.10612, 2019. [68] S. Zhang and G. Lin, “Robust data-driven discovery of governing physical laws with error bars,” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 474, no. 2217, p. 20180305, 2018. [69] W. Pan, Y. Yuan, J. Gon¸calves, and G. Stan, “A sparse Bayesian approach to the identification of nonlinear state-space systems,” IEEE Transactions on Automatic Control, vol. 61, no. 1, pp. 182–187, January 2016. [70] R. K. Niven, A. Mohammad-Djafari, L. Cordier, M. Abel, and M. Quade, “Bayesian identification of dynamical systems,” Multidisciplinary Digital Publishing Institute Proceedings, vol. 33, no. 1, p. 33, 2020. [71] M. Quade, “sparsereg - collection of modern sparse regression algorithms,” Feb. 2018. [Online]. Available: https://github.com/ohjeah/sparsereg