Redis ZSET 深度剖析:从命令、原理到实战
前言
Redis中的有序集合(Sorted Set或zset)是一种功能强大的数据结构,它结合了集合(Set)和哈希(Hash)的特点。与集合类似,zset包含的成员(member)是唯一的;但不同的是,zset中的每个成员都会关联一个浮点数类型的分数(score)。Redis正是通过这个分数来为集合中的成员进行排序。由于其有序的特性,zset在实现排行榜、优先级队列等需要排序功能的业务场景中扮演着至关重要的角色。本文将详细介绍zset的常用命令、内部编码方式及其典型的应用场景。
关于zset
zset有序集合:升序、降序
排序规则是啥
每个member都会安排一个分数
每个member都会安排一个分数
进行排序的时候,就是依照次数的分数大小进行升序/降序排序
因为是有序集合,所以zset中的memvber都是唯一的
zadd
添加或者更新指定的元素以及关联的分数到zset中,分数应该符合double类型,+int/-inf作为正负极限也是合法的
ZADD key [NX | XX] [GT | LT] [CH] [INCR] score member [score member]
ZADD相关选项:
- XX:仅仅⽤于更新已经存在的元素,不会添加新元素。
- NX:仅⽤于添加新元素,不会更新已经存在的元素。
- LT:只更新存在的元素,如果新的分数比当前分数小的话,那么这个更新才会成功的
- GT:只更新存在的元素,只有当新的根数比当前分数大,才会更新成功
- CH:默认情况下,ZADD 返回的是本次添加的元素个数,但指定这个选项之后,就会还包含本次更新的元素的个数。
- INCR:此时命令类似 ZINCRBY 的效果,将元素的分数加上指定的分数。此时只能指定⼀个元素和分数。
时间复杂度是O(log(n))
之前的hash、set、list很多时候,添加一个元素,都是O(1)时间复杂度,我们这里就是O(log(n))
由于zset是有序结构,要求新增的元素,要放到合适的位置上(找位置)
添加的时候既要添加元素,又要添加分数
member和score称为是一个pair,但是不是键值对那种的pair
对于有序结合,我们既可以听过member找到score
也能通过score找到member
这个有序集合可以存在两个相同的分数,但是member是唯一的
如果分数大小是一样的,那么我们就得按照元素自身字符串的字典序进行排序了
实际上,zset内部就是按照升序方式来排序的
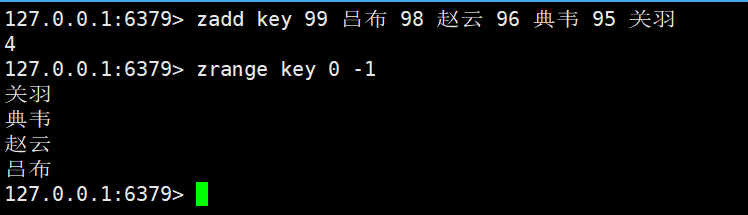
这里展示的效果就是升序的,从低到高的
进行数据的修改
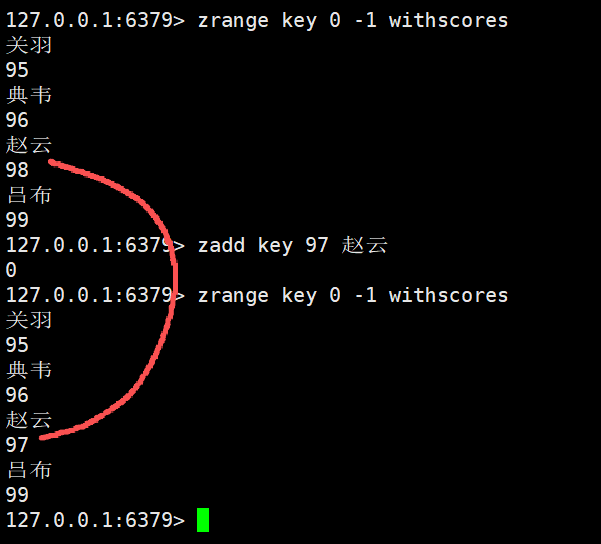
如果修改的分数,影响到了之前的顺序的话,就会自动的移动元素位置,保持原有的升序顺序不变
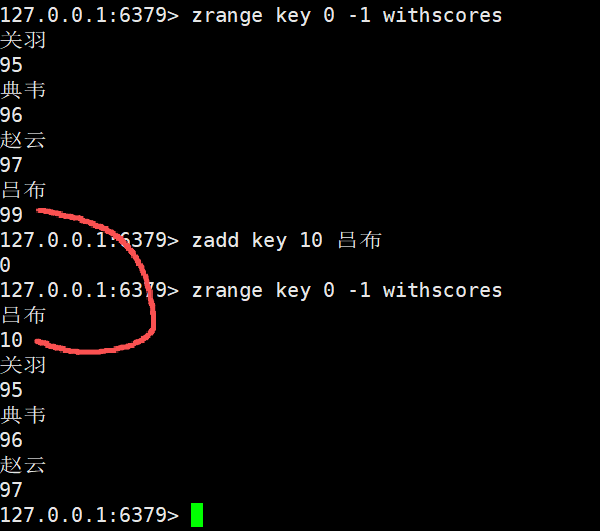
使用NX新增一个元素,
zadd key nx 94 张飞
返回值是1,说明我们已经成功新增了,并且也是按照升序自动排好了
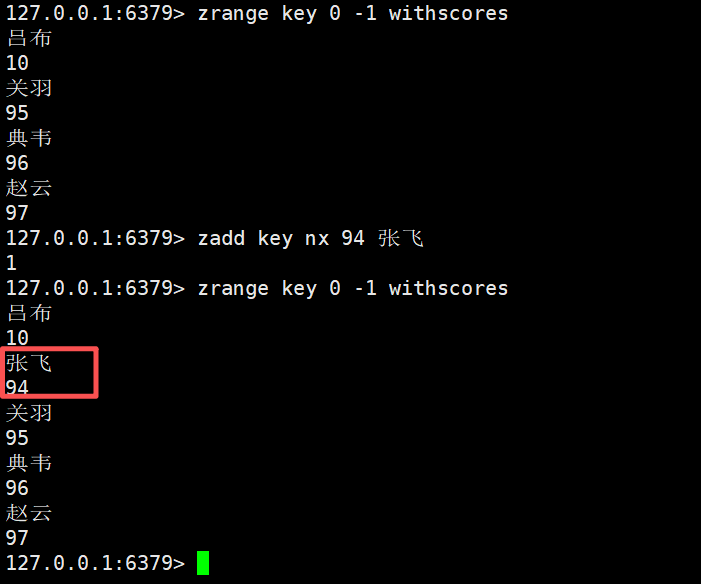
如果我们在nx选项的基础上,对已经存在的元素进行数据的修改,那么这个是不会修改成功的
因为nx选项是只会对不存在的元素进行创建行为
zadd key nx 100 张飞

xx选项就是只修改,不能进行新增,因为zadd是新增的操作命令,所以这里我们对元素进行修改是没有出现新增元素的,所以返回值是0,我们这里使用了xx选项进行了元素分数的修改操作了,并且进行了自动排序操作
zadd key xx 92 张飞
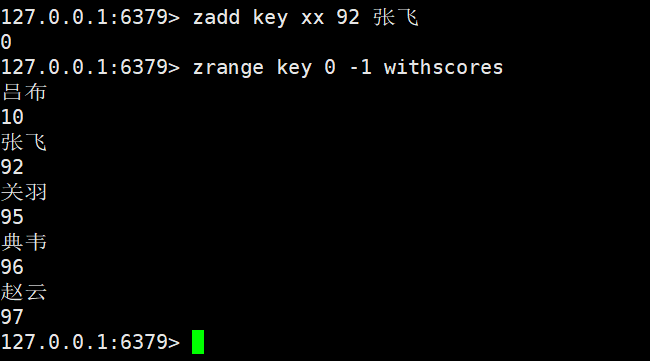
在xx选项的基础上进行元素的增加,返回值是0,所以我们这条命令是失败了的,xx命令只能进行存在元素的修改以及更新
zadd key xx 11 李四

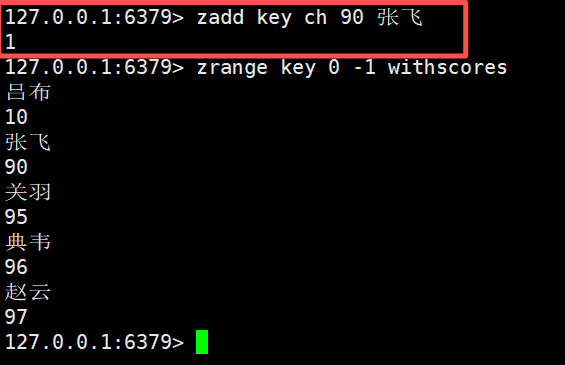
在ch选项的基础上,返回值除了添加元素的个数,还会带上更新元素的个数,比如说这里我对张飞这个元素进行更新了,所以这里的返回值1既包含了新增也包含了修改
zadd key ch 90 张飞
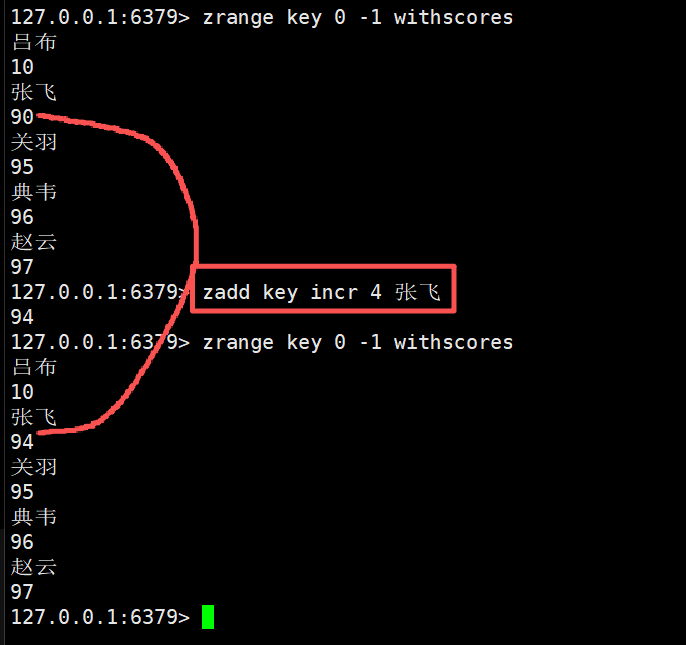
在选项incr的基础上,对指定的元素进行分数的增加,但是此时只能对一个元素进行修改了,不能对多个元素修改
并且这里的返回值是修改之后的分数大小
这里给张飞的分数加上4分
zadd key incr 4 张飞
zcard、zcount
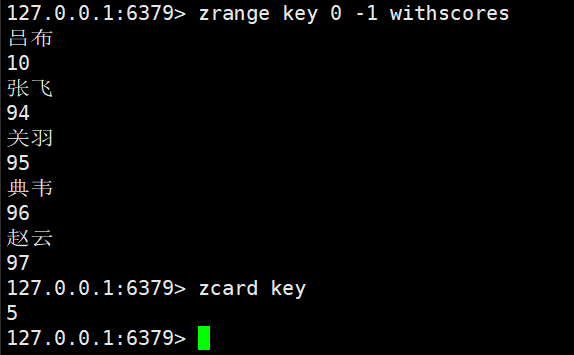
zcara:获取一个zset的基数,即zset中的元素个数
时间复杂度是O(1)
zset key
zcount :返回分数在min和max之间的元素个数,默认情况下,min和max是包含的,可以通过()排除
时间复杂度O(log(n))
返回值是满足条件的元素列表个数
指定min和max区间的,先根据min找到对应的元素
再根据max找到对应的元素
min和max是可以写成浮点数的(zset分数本身就是浮点数)
zcount key min max
默
认是一个闭区间
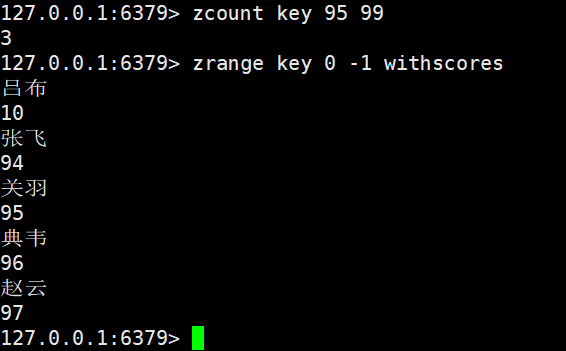
在这里加上一个左括号表示开区间
zcount key (95 99
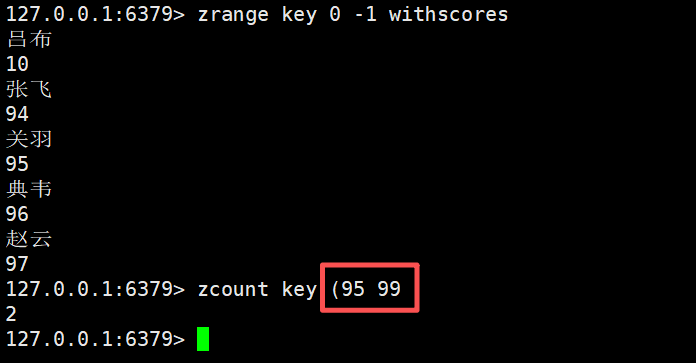
这个样子也可以

-inf表示负无穷大+inf表示正无穷大
这个会将区间内的数据都表示出来
zcount key -inf inf

zrange、zrevrange、zrangebyscore
使用zrange查看有序集合中的元素详情了
指定一对下标构成的区间
使用方法和我们之前学习到的range差不多
zrange key start stop [withscores]
时间复杂度是O(log(N)+M)
M是start和stop之间的元素个数
进行元素的添加以及出查询

但是我们这里只能看到member信息,不能看到对应的score
所以我们在后面加上选项withscores
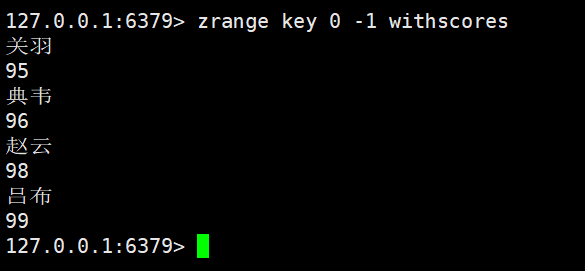
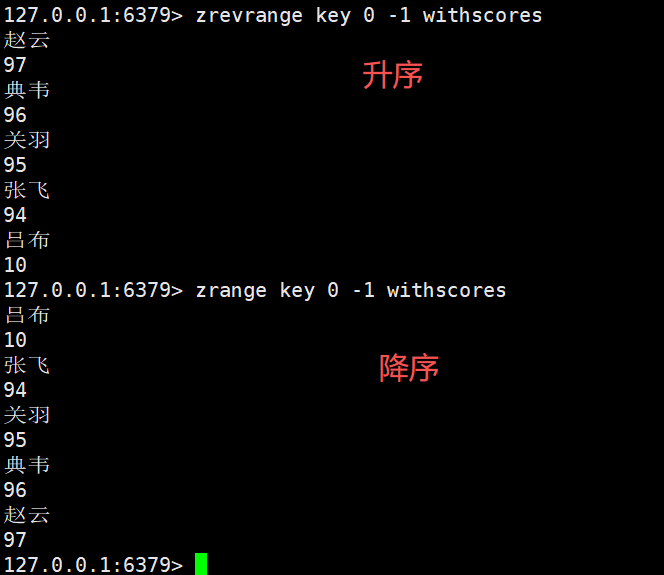
zrevrange:这里range前面多了个rev,其实就是reverse逆置的意思
默认的zrange是按照分数升序来进行排列的
我们加上rev就是按照分数降序进行排列的
zrevrange key start stop [withscores]
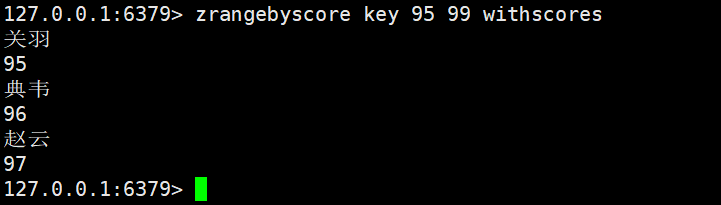
zrangebyscore:返回分数在min和max之间的元素,默认情况下,min和max都是包含的,可以通过(排除,就是开区间
按照分数来找元素的,相当于上面的zcount
zrangebyscore key min max [withscores]
时间复杂度O(log(N)+M)
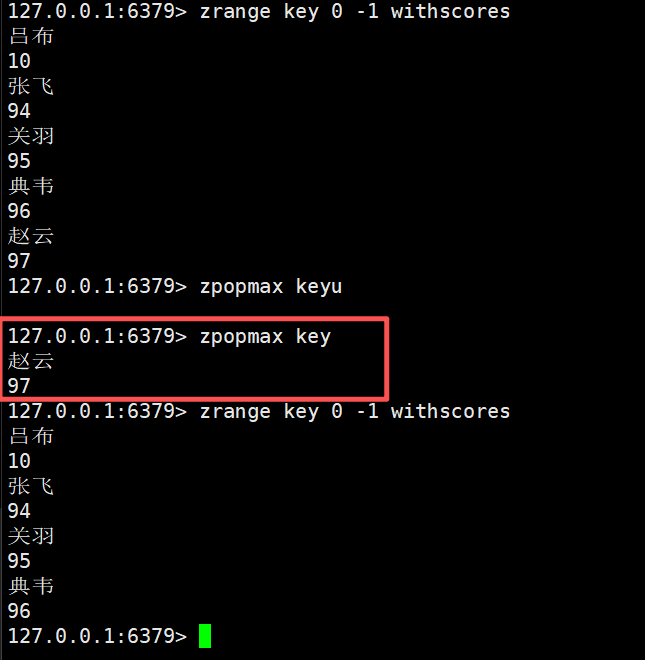
zpopmax
删除并返回分数最高的count个元素
zpopmax key [count]
时间复杂度O(log(N) * M)
N是有序集合的元素个数
M表示的是要删除的元素个数
返回的数据就是被删除的元素
加上count
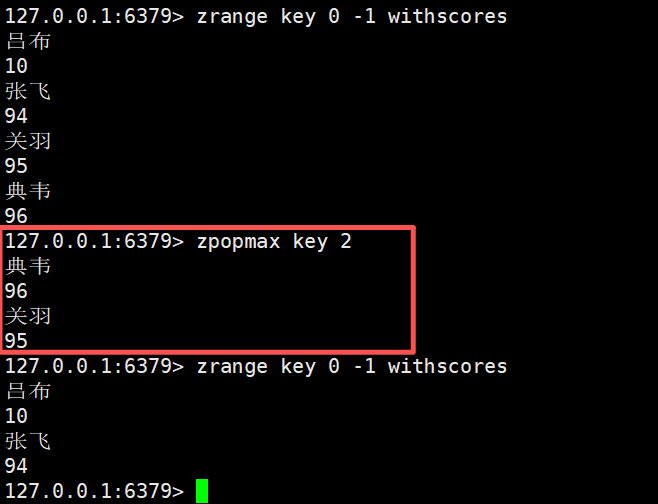
如果存在多个元素,分数相同,同为最大值,zpopmax删除的就是其中的一个元素
如果分数相同,那么就按照字典序进行排序
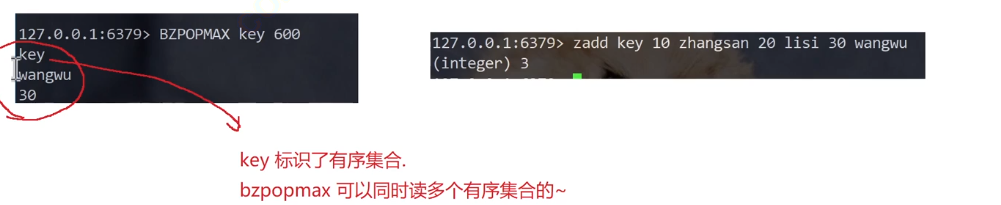
bzpopmax
时间复杂度是log(N)
删除最大值花的时间,使用通用的删除方法进行遍历
bzpopmax key [key...] timeout
我们这里的有序集合可以视为一个优先级队列,有的时候,也需要一个带有阻塞功能的优先级队列
每个key都是一个有序集合
阻塞也是在有序集合为空的时候出发阻塞,阻塞到有其他客户端插入元素
timeout表示的是超时时间,最多阻塞多久
类型是double类型的,单位是s,支持小数形式
zpopmin、bzpopmin
这里的两个命令和上面的zpopmax和bzpopmax是相对的
zpopmin:删除有序集合中最小的元素
时间复杂度是O(log(n) * M) M是count值
zpopmin key [count]
bzpopmin和bzopmax效果差不多
集合为空就会出现阻塞,直到客户插入数据就结束阻塞了
时间复杂度是log(n)
bzpopmin key [key...] timeout
zrank、zrevrank、zscore
zrank:返回指定元素的排名、升序,其实就是返回的是这个元素的下标
zrank key member
时间复杂度是log(n)
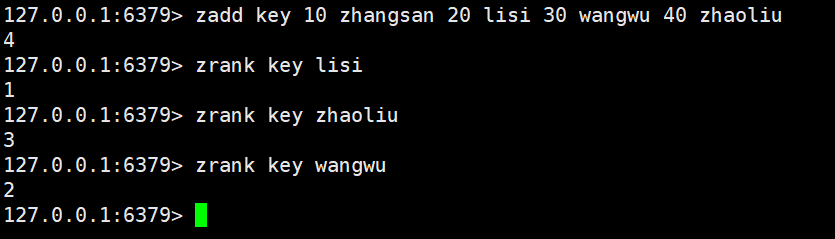
zrevrank:加上了rev,其实就是逆置,进行降序,返回指定元素的排名、降序
zrevrank key member
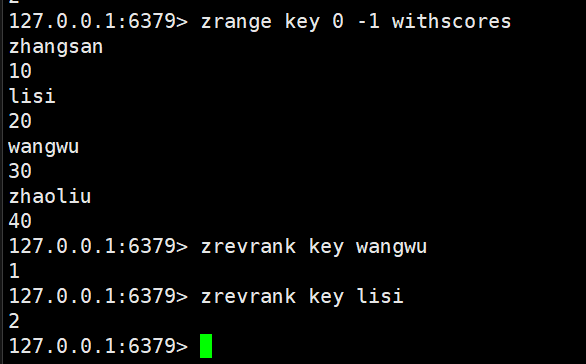
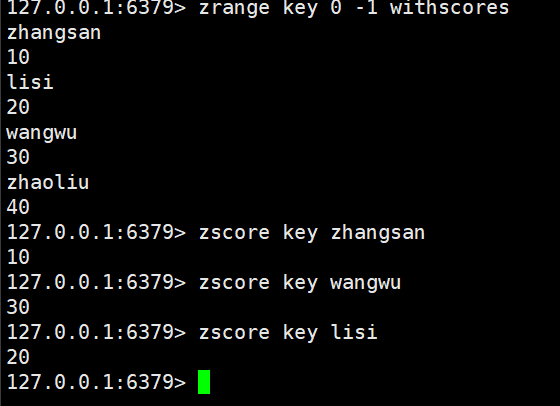
zscore:返回指定元素的分数
zscore key member
时间复杂度O(1),这里的时间复杂度是被优化了的
zrem、zremrangebyrank、zremrangebyscore
zrem:删除指定的元素
zrem key member [member...]
时间复杂度log(n)* m
m就是member个数
n是整个有序集合中元素的个数
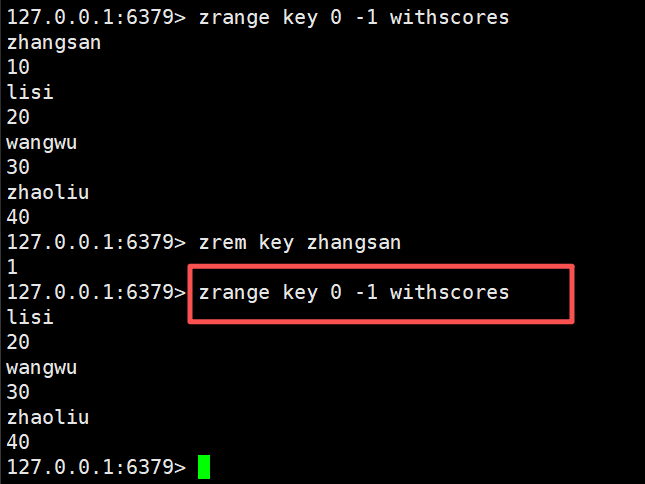
删了几个元素就返回几
zremrangebyrank:按照排序、升序删除指定范围的元素,左闭右闭
zremrangebyrank key start stop
使用这个下标描述的范围进行删除
时间复杂度是O(log(N+M))
N是整个有序集合的元素个数
M是start到stop区间中的元素
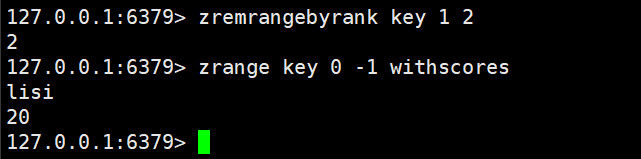
返回值就是删除的元素个数
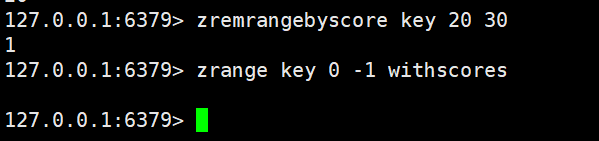
上面是根据下标进行元素删除的,那么我们这里的就是根据分数进行删除的
时间复杂度是O(log(N+M))
zremrangebyscore key min max
指定一个删除的区间,这个区间是通过分数来描述的
这个是一个闭区间
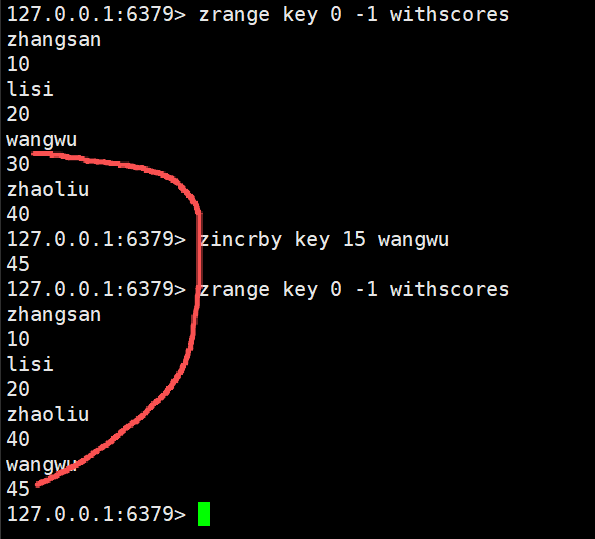
zincrby
为指定的元素的关联分数添加指定的分数值
正数和负数都可以的
浮点数也可以的
zincrby key increment member
zinterstore
sinter(交集)
sunion(并集)
sdiff(差集)
zinterstore:求交集,并将结果保存在另一个Key中
zinterstore destination numkeys key [key...] [weights weight [weight...]] [aggregate <sum | min | max]
时间复杂度是O(N * K )+O(M * log(M))
N是输入若干个有序集合,里面元素最小的个数
K是把几个有序集合求交集
M是最终结果的个数
destination就是结果存放的key
numkeys是一个数字,描述了后续有几个key参与交集运算
numkeys描述出key的个数之后,就可以明确的知道,后面的选项是从哪里开始了,避免选项和keys混淆
这个和我们的Http协议很相似
报文中存在一个content-length,表示的是正文的长度
如果没有这个的话就会出现粘包问题出现
粘包问题是面向字节流这种IO方式中的一个普遍存在的问题
文件读写也会出现这种粘包问题
解决粘包问题:
1、明确包的长度
2、明确包的边界
zinterstore destination numkeys key [key...] [weights weight [weight...]] [aggregate <sum | min | max]
weights:权重
aggregate:描述的是在member相同的时候,分数合并的时候应该按照什么方式进行合并
在进行比较相同的时候,只要member相同即可,score不一样无所谓,我们比较的是member
如果member相同,score不同,进行交集合并之后的最终分数咋算
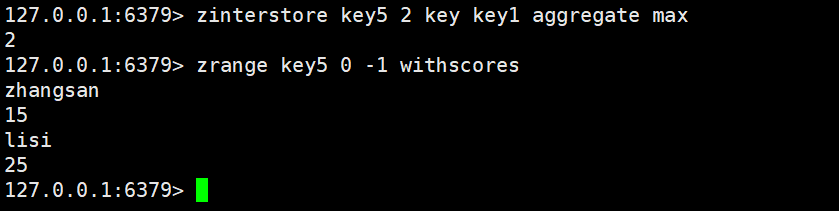
那么我们的aggregate就起到了作用了,这里存在三种模式:sum、min、max
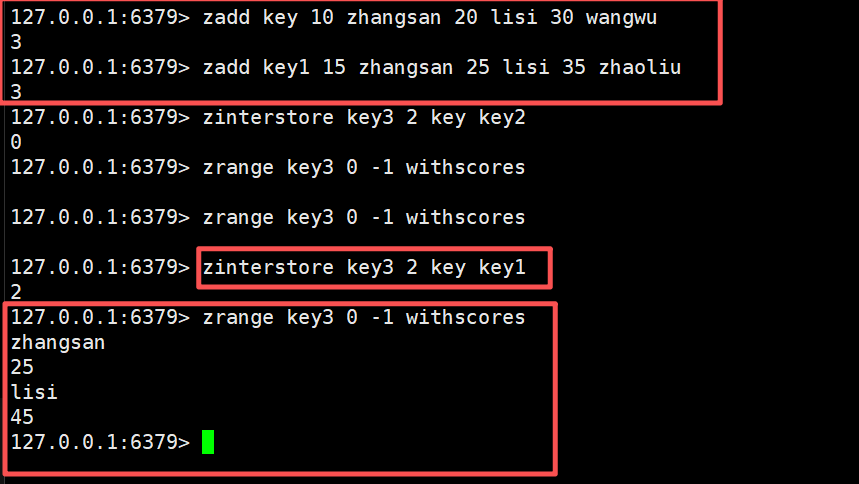
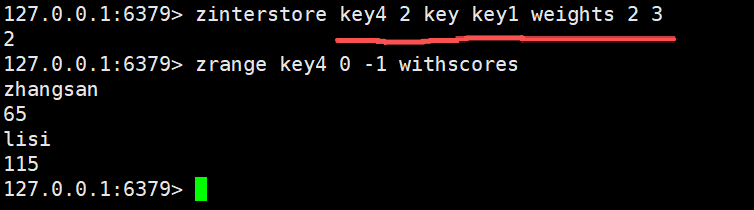
这里我们在命令中加上权重,设置两个权重值,然后每个权重值和对应key中的数据进行相乘,最后将计算权重后的数据进行合并处理操作
zinterstore key4 2 key key1 weights 2 3
在后面加上aggregate
zunionstore
求并集,并将结果保存在另一个Key中
zunionstore destination numkeys key [key...] [weights weight [weight...]] [aggregate <sum | min | max]
destination存放结果的key
numkeys是表示我们当前有几个比较的集合
weights用来表示每个集合的权重是多少,在计算的时候,比较的是计算好权重值之后的数据的
aggregate描述我们遇到相同元素是求和还是求最小值还是取最大值
命令小结
好的,这是根据您提供的图片生成的表格内容:
| 命令 | 时间复杂度 |
|---|---|
| zadd key score member [score member …] | O(k * log(n)), k 是添加成员的个数, n 是当前有序集合的元素个数 |
| zcard key | O(1) |
| zscore key member | O(1) |
| zrank key member zrevrank key member | O(log(n)), n 是当前有序集合的元素个数 |
| zrem key member [member …] | O(k * log(n)), k 是删除成员的个数, n 是当前有序集合的元素个数 |
| zincrby key increment member | O(log(n)), n 是当前有序集合的元素个数 |
| zrange key start end [withscores] zrevrange key start end [withscores] | O(k + log(n)), k 是获取成员的个数, n 是当前有序集合的元素个数 |
| zrangebyscore key min max [withscores] zrevrangebyscore key max min [withscores] | O(k + log(n)), k 是获取成员的个数, n 是当前有序集合的元素个数 |
| zcount | O(log(n)), n 是当前有序集合的元素个数 |
| zremrangebyrank key start end | O(k + log(n)), k 是获取成员的个数, n 是当前有序集合的元素个数 |
| zremrangebyscore key min max | O(k + log(n)), k 是获取成员的个数, n 是当前有序集合的元素个数 |
| zinterstore destination numkeys key [key …] | O(n * k) + O(m * log(m)), n 是输入的集合最小的元素个数, k 是集合个数, m 是目标集合元素个数 |
| zunionstore destination numkeys key [key …] | O(n) + O(m * log(m)), n 是输入集合总元素个数, m 是目标集合元素个数 |
编码方式
如果有序集合中的元素格式比较少,或者单个元素体积比较小,使用ziplist来存储
压缩列表,节省空间
如果元素个数多,或者单个元素的体积大,使用skiplist进行存储
我们可以使用命令进行查看编码方式
object encoding key
跳表是一个复杂链表
相比树型结构,更适合按照范围获取元素
查询元素,时间复杂度logN
应用场景
排行榜系统
1、微博热搜
2、游戏天梯排行
3、成绩排行
总结
有序集合(ZSET)是Redis中一种非常重要且功能丰富的数据结构。本文深入探讨了ZSET的核心概念与操作命令。
核心要点回顾:
-
数据结构特性:ZSET是一个不含重复成员的集合,其中每个成员都关联一个分数,并根据这个分数自动进行升序排序。如果分数相同,则按成员的字典序排序。
-
核心命令:我们学习了ZSET的一系列操作命令,涵盖了从基础的增删改查(如ZADD, ZREM, ZSCORE, ZINCRBY)到范围查询(如ZRANGE, ZRANGEBYSCORE)和排名获取(如ZRANK, ZREVRANK)。
-
高级操作:文章还介绍了更高级的命令,包括弹出最大/最小成员(ZPOPMAX, ZPOPMIN)及其阻塞版本(BZPOPMAX, BZPOPMIN),以及强大的集合间运算(ZINTERSTORE, ZUNIONSTORE),这些命令可以方便地处理复杂的业务逻辑。
-
内部编码:ZSET的底层实现会根据数据规模在ziplist(压缩列表)和skiplist(跳表)之间智能切换,以在保证性能的同时优化内存使用。
-
应用场景:凭借其高效的排序能力,ZSET是构建排行榜系统(如热搜榜、游戏天梯)等场景的理想选择。
总而言之,ZSET凭借其“有序”和“集合”的双重特性,在Redis的五大数据类型中占据了独特的地位,掌握其用法对于开发高性能的Redis应用至关重要。
