什么是多元线性回归，系数、自变量、因变量是什么，多元线性回归中的线性是什么

1️⃣ 什么是多元线性回归

• 定义：多元线性回归（Multiple Linear Regression, MLR）是一种统计建模方法，用来研究一个因变量与两个或以上自变量之间的关系。

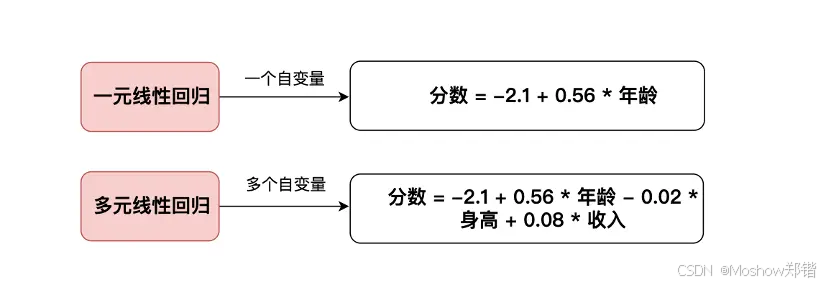
• 目标：通过拟合一条（在高维空间中是一个超平面）来预测或解释因变量的变化。

• 数学形式：

• 

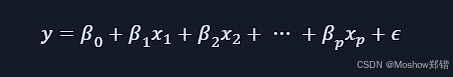
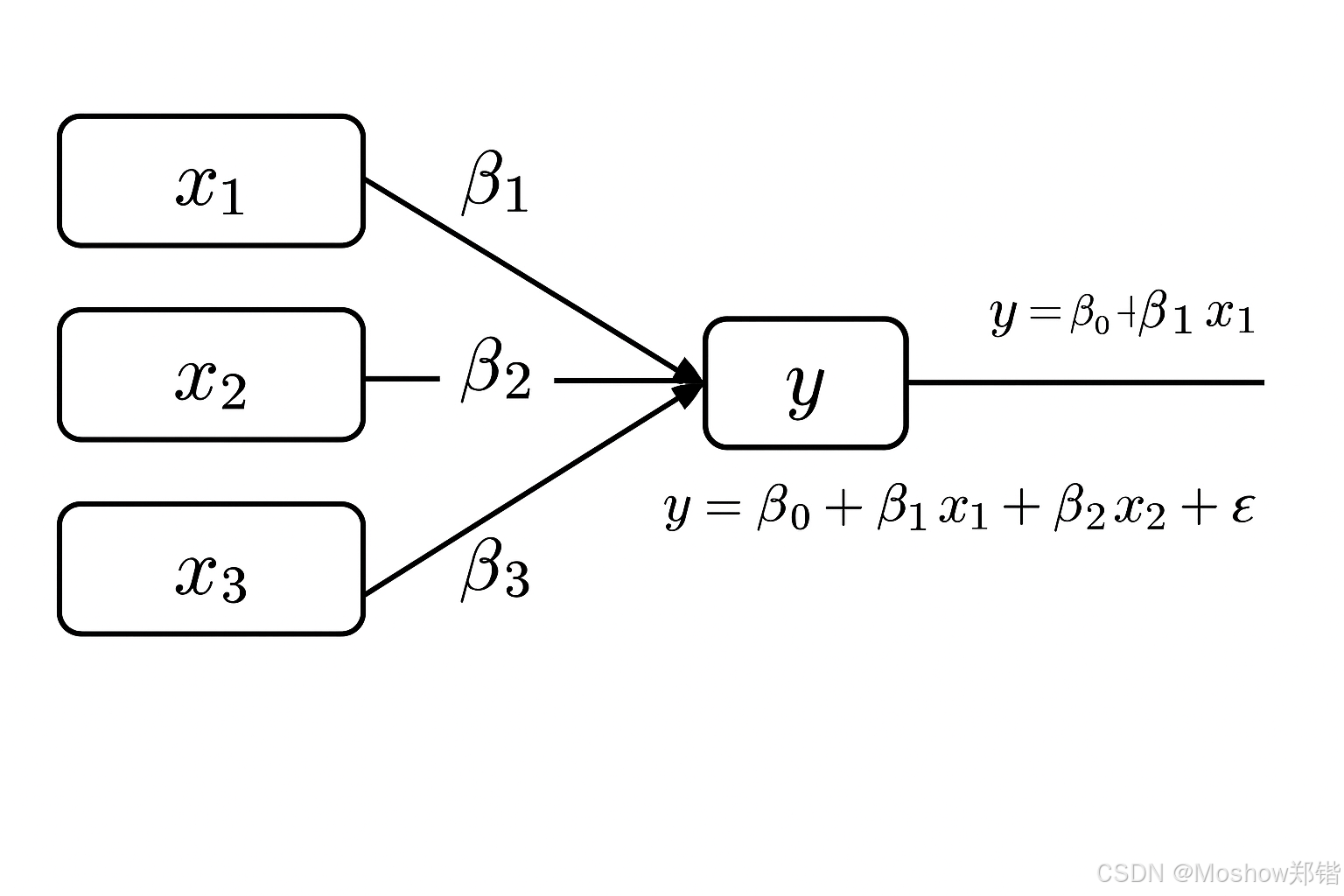
其中：

2️⃣ 系数（Coefficient）🪐

• 含义：每个自变量对因变量的影响大小和方向。

• 正系数：自变量增加，因变量也增加（正相关）。

• 负系数：自变量增加，因变量减少（负相关）。

• 绝对值大小：影响强弱（需在同一量纲下比较）。

• 例子： 如果房价模型中“面积”的系数是 3，表示面积每增加 1 单位，房价平均增加 3 个单位（假设单位是万元）。

3️⃣ 自变量（Independent Variable）

• 定义：模型的输入特征，用来解释或预测因变量。

• 特点：在统计假设中，它们不依赖于因变量。

• 例子：房价预测中的面积、卧室数、楼层、地段评分等。

4️⃣ 因变量（Dependent Variable）

• 定义：模型要预测或解释的目标变量，也叫响应变量（Response Variable）或标签（Label）。

• 例子：房价预测中的“房价”。

5️⃣ 多元线性回归中的“线性”是什么意思

• 不是指自变量必须是直线关系，而是指模型对系数是线性的。

• 形式是自变量的加权和（加上常数项），权重就是系数。

• 即使自变量是平方项、对数项，只要系数是一次方，模型依然是“线性回归”。

• 例子：

  • 线性回归：

y=2+3x1−5x2y = 2 + 3x_1 - 5x_2

• 依然是线性回归（虽然有平方项）：

y=2+3x1+4x22y = 2 + 3x_1 + 4x_2^2

因为系数 3 和 4 仍然是一次方。

💡 一句话总结：

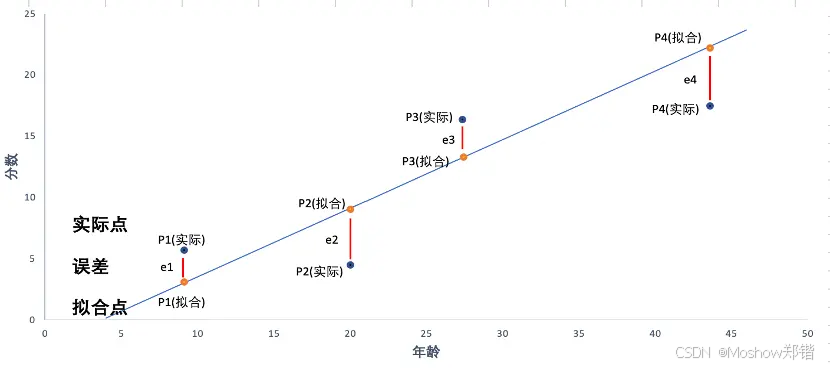
多元线性回归就是用多个特征的加权和去预测一个目标，系数告诉你每个特征的影响方向和大小，“线性”是指模型对系数的线性关系，而不是对变量值的线性关系。