随机森林1
如果聚合一组预测器(比如分类器或回归器)的预测,得到的预测结果比最好的单个预测器要好,这样的一组预测器成为集成。而一个集成学习的算法则成为集成方法。
这就说明:即使每个分类器都是弱学习器,通过集成依然可以实现一个强学习器(高精度),只要有足够大数量并且足够多种类的弱学习器就可以。
例如:可以训练一组决策树分类器,每棵树都基于训练集不同的随机子集进行训练,然后可以获得所有个体树的预测,获得最多选票的类是集成预测的结果。这样一组决策树的集成被称为随机森林。
一、硬投票和软投票
1、硬投票和软投票的介绍
假设已经训练好了一些分类器,每个分类器的精度约为80%。大概包括:一个逻辑回归分类器、一个SVM分类器、一个随机森林分类器、一个k近邻分类器,或许还有更多。 创建更好分类器的一种非常简单的方法是聚合每个分类器的预测:获得最多选票的类是集成的预测。这种多数投票分类器称为硬投票分类器 。
投票分类器的精度通常比集成中最好的分类器还要高。但是,这基于的前提是:所有的分类器都是完全独立的,彼此的错误毫不相关。
分类器不可能完全独立,因为它们都是在相同的数据上训练的。它们很可能会犯相同的错误,所以也会有很多次大多数投给了错误的类,导致集成的精度有所降低。
想要预测器尽可能相互独立,集成方法的效果最优,可以使用不同的算法进行训练。这会增加它们犯不同类型错误的机会,从而提升集成的精度。
import matplotlib.pyplot as plt
import numpy as np
from nltk import extractheads_proba = 0.51 # 设置硬币正面朝上的概率为0.51
np.random.seed(42)
# 将随机数与0.51比较,小于0.51的记为1(正面),否则为0(反面),生成10000次抛掷、10组实验的二进制结果矩阵。
coin_tosses = (np.random.rand(10000, 10) < heads_proba).astype(np.int32)# 计算每组实验正面的数字
cumulative_heads = coin_tosses.cumsum(axis=0)
# 用累计正面数除以抛掷次数(1到10000),得到每组实验的正面比例随时间的变化
cumulative_heads_ratio = cumulative_heads / np.arange(1, 10001).reshape(-1, 1)plt.figure(figsize=(8, 3.5))
plt.plot(cumulative_heads_ratio)
plt.plot([0, 10000], [0.51, 0.51], "k--", linewidth=2, label="51%")
plt.plot([0, 10000], [0.5, 0.5], "k-", label="50%")
plt.xlabel("Number of coin tosses")
plt.ylabel("Heads ratio")
plt.legend(loc="lower right")
plt.axis([0, 10000, 0.42, 0.58])
plt.grid()
plt.show()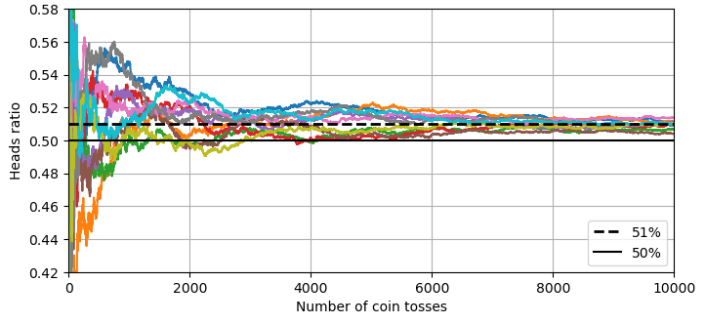
如果所有的分类器都能够估计 类概率(都有predict_proba()方法),那么可以预测具有最高类概率的类,对所有单独的分类器进行平均,这称为软投票。它通常比硬投票能或的更高的性能,因为他给高度自信(权重高)的投票更多的权重。
2、VotingClassifier类的使用
VotingClassifier类是一种集成方法,通过组合多个分类器的预测结果,通常投票获得比单一分类器更好的结果。
其工作流程为:训练多个不同的基分类器 → 对每个样本,收集所有分类器的预测结果 → 根据投票规则确定最终预测结果
VotingClassifier类的参数:
estimators:传入包含(名称, 估计器)元组的列表,例如:[(名称1,估计器1),(名称2,估计器2)]
voting:传入 hard 或 soft 两种投票方式,默认是hard投票。在使用soft投票的时候需要保证克隆的估计器都能够计算类概率,即有predict_proba()方法,参数probability=True。
weights:给各分类器分配权重(列表或数组)
n_jobs:并行运行的作业数,-1表示使用所有可用的CPU核心进行并行计算,默认是1 表示不适用并行计算
X, y = make_moons(n_samples=500, noise=0.30, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)voting_clf = VotingClassifier(estimators=[('lr', LogisticRegression(random_state=42)),('rf', RandomForestClassifier(random_state=42)),('svc', SVC(random_state=42))]
)
voting_clf.fit(X_train, y_train)当拟合VotingClassifier时,他会克隆每个估计器并拟合这个克隆,原始估计器列表可通过estimators属性获得,而克隆的每个估计器可通过estimators_属性获得。想要获得原始估计器字典的话就可以通过named_estimators或named_estimators_获得。
voting_clf.estimators_
# [LogisticRegression(random_state=42),
# RandomForestClassifier(random_state=42),
# SVC(random_state=42)]voting_clf.estimators
# [('lr', LogisticRegression(random_state=42)),
# ('rf', RandomForestClassifier(random_state=42)),
# ('svc', SVC(random_state=42))]voting_clf.named_estimators
# {'lr': LogisticRegression(random_state=42),
# 'rf': RandomForestClassifier(random_state=42),
# 'svc': SVC(random_state=42)}| 特性 | 硬投票(Hard Voting) | 软投票(Soft Voting) |
|---|---|---|
| 输入要求 | 基模型输出类别标签(predict) | 基模型输出概率(predict_proba) |
| 决策方式 | 根据标签进行投票比较 | 根据类别概率加权平均之后进行比较 |
| 适用模型 | 所有分类器 | 仅限支持概率输出的分类器(如逻辑回归、随机森林) |
| 抗噪声能力 | 较强(直接投票忽略低置信度预测) | 较弱(低概率预测仍影响结果) |
| 结果解释性 | 更直观(直接计数) | 更细腻(考虑预测置信度) |
二、随机森林的随机性
随机森林的随机核心主要通过两种机制来保证:数据随机性(随机采样数据)和特征随机性
1、随机采样:bagging、pasting
(1)bagging\pasting理论介绍
第一部分通过获取不同种类分类器的方法得到不同的训练算法,最终通过投票集成预测结果,从而提高准确率。
还可以通过使用相同的算法,但是在不同的训练集随机子集上进行训练,最后将得到的预测结果进行集成(集成操作通常是由聚合函数(分类的统计模型或平均法)完成的),提高准确率(每个预测器单的的偏差都高于在原始训练集上训练的偏差,通过聚合同时降低偏差的方差)。随机子集的采样分为两种:有放回的采样bagging、不放回采样pasting。
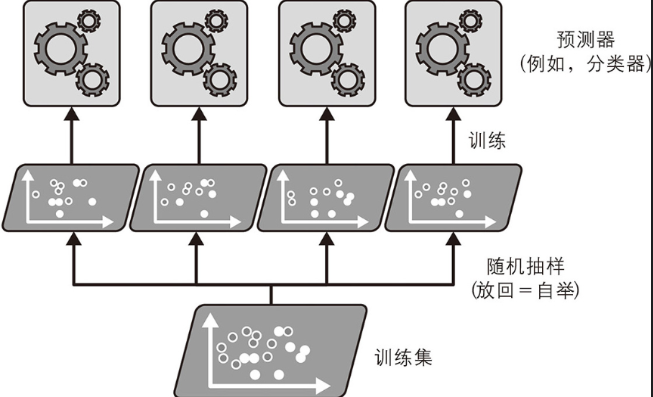
(2)包外评估
对于任意给定的预测器,使用bagging,有些训练实例可能会被采样多次,而有些实例可能根本不被采样,这样未被采样的训练实例称为Out of bag (包外实例,对于预测器来说包外实例是不一样的)。
例如:BaggingClassifier类默认采样m个训练实例,然后使用放回样本(bootstrap=True)。在数学上表明:对每个预测器来说,平均只对63%的训练实例进行采样,剩余的37%(m个训练集,每个样本被选中的概率是 ,不被选中的概率为
,那么每次都不被选中的概率就是
,m 越大这个概率越接近
约为37%),训练实例(包外实例)未被采样。
bagging集成可以使用OOB(OUT OF BAG)实例进行评估,而不需要单独的验证集,只要有足够多的估计器,那么训练集中的每个实例都可能是多个估计器的OOB实例,因此可以使用这些估计器为该实例做出公平的集成预测,可以计算集成的预测精度。
在sklearn中,创建BaggingClassifier时,设置obb_score=True,可以请求在训练结束后自动进行包外评估。
小总结:由于自举法给每个预测器的训练子集引入更高的多样性,因此有放回的bagging比无放回的pasting的偏差略高,这就意味着预测器预测器之间的关联度更低,所以集成的方差会降低。也就是说bagging生成的模型通常更好。
在选择bagging和pasting的时候,花费一定的时间的CPU资源进行交叉验证来对两种结果进行评估,在做出最合适的选择。
2、随机特征采样——随机补丁和随机子空间
(1)随机子空间和随机补丁的介绍
BaggingClassifier类也可以对特征进行采样,由max_features和bootstrap_features两个超参数控制,每个预测器用输入特征的随机子集进行训练。当处理高维输入的时候,此技术可以减少训练特征大大加快训练速度。
随机子空间:值随机化特征,而不随机化数据。也就是说每个基础估计器都在原始训练集的全部样本上进行训练(bootstrap=False,max_samples=1.0),但使用的特征是从所有特征中随机选出的特征子集(bootstrap_features = True,max_features < 1.0 )。
随机补丁方法:同时对训练样本和特征继续宁随机采样
(2)BaggingClassifier类的使用
BaggingClassifier工作流程:随机采样 → 并行训练(同一算法在不同子数据集上训练一个模型) → 集体决策(投票)
BaggingClassifier类的参数介绍:
estimator:基础估计器
n_estimator:基础估计器数量,也可以理解成要随机抽取多少次
max_samples:要随机抽取的样本数量(比例或绝对数)
bootstrap:是否有放回的抽取样本数量,默认是True表示有放回的采样数据
obb_score:是否使用包外评估,默认是False不使用
max_features:要随机抽取的特征数量(比例或绝对数)
bootstrap_features:是否有放回的的抽取特征数量,默认是False不放回
n_jobs,random_state...
如果基础分类器可以估计类概率[具有predict_proba()方法],则BaggingClassifier自动执行软投票而不是硬投票 。
bag_clf = BaggingClassifier(DecisionTreeClassifier(), n_estimators=1000,max_samples= 20 ,bootstrap= True,bootstrap_features=True oob_score=Truen_jobs=-1, random_state=42)
bag_clf.fit(X_train, y_train)
bag_clf.obb_score_ # 请求包外评估分数
def plot_decision_boundary(clf, X, y, alpha=1.0):axes=[-1.5, 2.4, -1, 1.5]x1, x2 = np.meshgrid(np.linspace(axes[0], axes[1], 100),np.linspace(axes[2], axes[3], 100))X_new = np.c_[x1.ravel(), x2.ravel()]y_pred = clf.predict(X_new).reshape(x1.shape)plt.contourf(x1, x2, y_pred, alpha=0.3 * alpha, cmap='Wistia')plt.contour(x1, x2, y_pred, cmap="Greys", alpha=0.8 * alpha)colors = ["#78785c", "#c47b27"]markers = ("o", "^")for idx in (0, 1):plt.plot(X[:, 0][y == idx], X[:, 1][y == idx],color=colors[idx], marker=markers[idx], linestyle="none")plt.axis(axes)plt.xlabel(r"$x_1$")plt.ylabel(r"$x_2$", rotation=0)tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)fig, axes = plt.subplots(ncols=2, figsize=(10, 4), sharey=True)
plt.sca(axes[0])
plot_decision_boundary(tree_clf, X_train, y_train)
plt.title("Decision Tree")
plt.sca(axes[1])
plot_decision_boundary(bag_clf, X_train, y_train)
plt.title("Decision Trees with Bagging")
plt.ylabel("")
plt.show()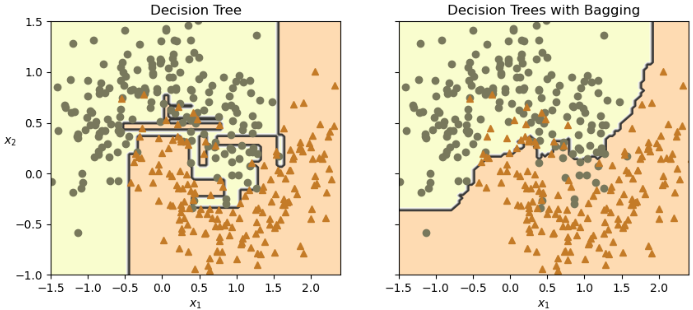
由上图可以看出:集成预测的泛化效果会比单独的决策树要好一些:二者偏差相近,但是集成的方差更小(两边训练集上的错误数量差不多,但是集成的决策边界更规则)。
三、随机森林
1、理论介绍
随机森林是决策树的集合,通常通过bagging方法(有时候pasting方法)进行训练,将max_samples设置为训练集的大小。
第二部分通过构建BaggingClassifier并向其传递DecisionTreeClassifier实现随机森林的分类预测。在sklearn中可以使用RandomForestClassifier,直接实现随机森林的效果 。它更方便并且针对决策树进行了优化(类似地,有一个用于回归任务的RandomForestRegressor类)。该类具有DecisionTreeClassifier的所有超参数(以控制树的生长方式),以及BaggingClassifier的所有超参数来控制集成本身。
bcd = BaggingClassifier(DecisionTreeClassifier(max_features= "sqrt",max_leaf_nodes= 16),n_estimators=500,random_state=42,n_jobs=-1)
bcd.fit(X_train, y_train)
y_pred_bcd = bcd.predict(X_test)2、RandomForestClassifier类的使用
RandomForestClassifier类的参数:
n_estimators:森林中树的数量,默认是100
criterion:树的分裂质量的衡量标准,gini或entropy
max_depth:树的最大深度,None表示节点扩展直到所有叶子都是纯的或包含的样本数小于min_samples_split
min_samples_split:分裂节点所需要的最小样本数量
min_samples_leaf:叶节点的最小样本数量
max_features:最佳分裂时考虑特征数量。sqrt(总数开平方的数);log2(log2(特征总数));int(指定的特征数量);float(总特征数×该比例);None(考虑所有特征)
bootstrap:是否使用bootstrap采样构建树,默认时True;
random_state:控制随机性
rnd_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16,n_jobs=-1, random_state=42)
rnd_clf.fit(X_train, y_train)
y_pred_rf = rnd_clf.predict(X_test)增加随机森林的随机性也就是提高预测多样性,就是用高偏差(预测值和真实值之间的差)换取低方差(模型对训练数据的微小变化)
四、极端随机森林
1、极端随机森林的介绍
随机森林是数据随机性、特征随机性双重随机性来构架的决策树集合。想要进一步的提高随机性可以在节点分裂时对每个特征使用随机阈值,而不是搜索得出的最佳阈值 (只需在创建DecisionTreeClassifier时设置splitter="random"), 这种极端随机的决策树组成的森林,被称为极端随机森林。
同样,它也是以更高的偏差换取了更低的方差。 极端随机树训练起来比常规随机森林要快很多,因为在每个节点上找到每个特征的最佳阈值是决策树生长中最耗时的任务之一。但使用的时候其参数和随机森林是相同的。
2、ExtraTreesClassifier类的使用
ExtraTreesClassifier类的参数:
criterion:分裂标准,gini或entropy(信息增益)
splitter:分裂策略,必须设置为random。这是和决策树的关键区别之一
max_depth:最大深度
min_samples_split:内部节点在分裂所需的最小样本数量
min_samples_leaf:叶节点的最小样本数量
max_features:分裂的时候考虑的最大特征数
class_weight:类别权重,用于处理不平衡的数据集,设置为balanced来自动调整权重
etr = ExtraTreesClassifier(n_estimators=500, max_leaf_nodes=16, n_jobs=-1, random_state=42)
etr.fit(X_train, y_train)
# etr.score(X_test,y_test) # R2分数
y_pred_etr = etr.predict(X_test)3、极端随机森林和随机森林的比较
| 特性 | RandomForestClassifier (RF) | ExtraTreesClassifier、ExtraTreeClassifier |
|---|---|---|
| 全称 | 随机森林 | 极端随机树/森林 |
| 基学习器 | DecisionTreeClassifier (分裂器为 best) | ExtraTreeClassifier (分裂器为 random) |
| 分裂策略 | 最佳分裂:对于每个特征,考虑所有可能的分裂点,选择最优的一个(如基尼系数下降最多)。 | 随机分裂:对于每个特征,随机生成若干个分裂点,然后从这些随机点中选择最优的一个。 |
| 样本使用 | 默认使用 Bootstrap采样(有放回抽样),每棵树的训练数据是原始数据集的一个子集。 | 默认使用全部训练样本(但可通过 bootstrap=True 改为Bootstrap采样)。 |
| 随机性来源 | 1. 行随机(Bootstrap) 2. 列随机( max_features) | 1. 行随机(默认无,但可开启) 2. 列随机( max_features)3. 分裂点随机(核心区别) |
| 计算速度 | 较慢。需要为每个特征计算所有可能分裂点的指标,计算成本高。 | 显著更快。避免了计算所有分裂点的开销,只需要评估少量随机分裂点。 |
| 偏差-方差 | 偏差较低,方差较低。 | 偏差稍高(因为分裂不是全局最优),方差更低(因为更强的随机性进一步破坏了相关性)。 |
| 过拟合倾向 | 抗过拟合能力很强。 | 抗过拟合能力通常更强,尤其在高维噪声数据上表现更鲁棒。 |
| 如何选择 | 数据质量较高,需要分析单棵树 | 数据量非常大的时候,担心过拟合, |
如果想要知道极端随机数和随机森林哪个预测效果更好需要通过交叉验证进行比较。
