算法训练营day59 图论⑨ dijkstra(堆优化版)精讲、Bellman_ford 算法精讲
继续最短路径算法,优化篇!!
dijkstra(堆优化版)精讲
在上一篇中,我们讲解了朴素版的dijkstra,该解法的时间复杂度为 O(n^2),(两层嵌套的for循环)可以看出时间复杂度 只和 n (节点数量)有关系。
这么在n 很大的时候,也有另一个思考维度,即:从边的数量出发。n 很大,边 的数量 很小的时候(稀疏图)
之前是 通过遍历节点来遍历边,通过两层for循环来寻找距离源点最近节点。 这次我们直接遍历边,且通过堆来对边进行排序,达到直接选择距离源点最近节点。其实和我们之前的kruskal算法精讲很相似,简单复习之前的这个算法使用的是并查集
在之前版本的实现思路中,我们提到了三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
那么当从 边 的角度出发, 在处理 三部曲里的第一步(选源点到哪个节点近且该节点未被访问过)的时候 ,我们可以不用去遍历所有节点了。而且 直接把 边(带权值)加入到 小顶堆(利用堆来自动排序),那么每次我们从 堆顶里 取出 边 自然就是 距离源点最近的节点所在的边。这样我们就不需要两层for循环来寻找最近的节点了。
数据存储方式如下:pair<int, int> 第一个int 表示所连接的节点,第二个int表示该边的权值
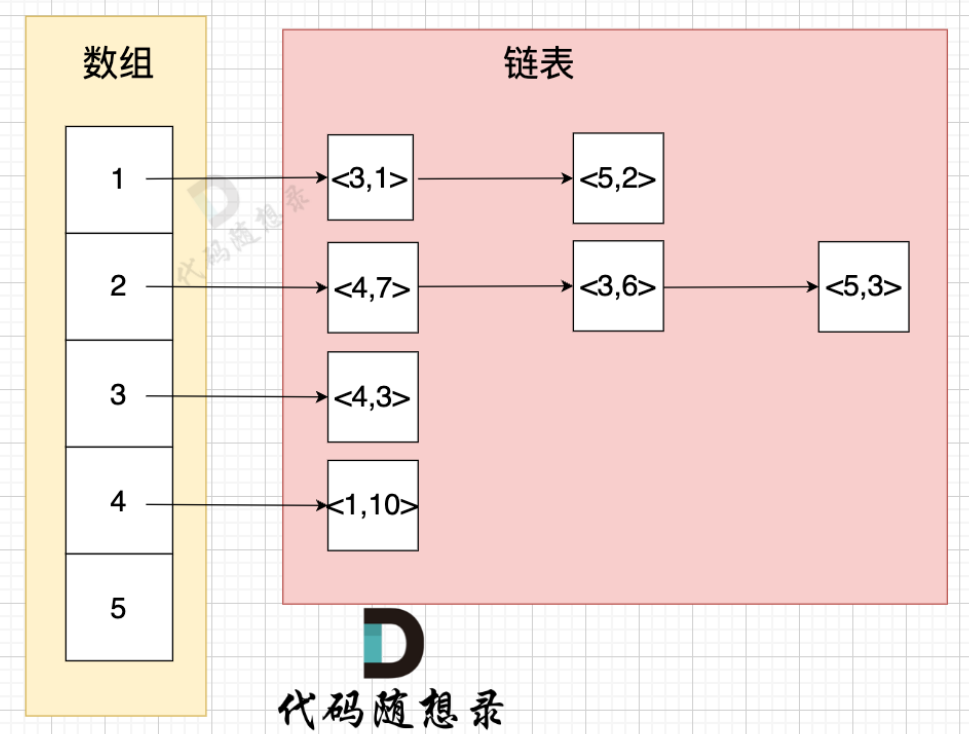
在代码实现过程中,重点是采用了不同的数据结构(堆),同时具体过程中有三种列表(具体见下图,可能会混淆,需要对于变量含义的深刻理解)
这个地方用到了堆,但是没有排序的部分,大家不要惯性思维,使用堆来实现通过遍历边来实现最短路径
# 导入堆队列模块,用于实现优先队列
import heapq# 定义边(Edge)类,用于表示图中的一条边
class Edge:def __init__(self, to, val):self.to = to # 边的目标节点self.val = val # 边的权重(距离)def dijkstra(n, m, edges, start, end):"""Dijkstra算法实现,求解从起点到终点的最短路径参数:n: 节点总数m: 边的总数edges: 边的列表,每个元素为(p1, p2, val)表示从p1到p2的边,权重为valstart: 起点end: 终点返回:起点到终点的最短距离,如果不可达则返回-1"""# 构建邻接表表示图,grid[i]存储所有从节点i出发的边grid = [[] for _ in range(n + 1)] # 节点编号从1开始,所以+1# 遍历所有边,填充邻接表for p1, p2, val in edges:grid[p1].append(Edge(p2, val))# 存储从起点到每个节点的最短距离,初始化为无穷大minDist = [float('inf')] * (n + 1)# 记录节点是否已被访问(即是否已确定最短路径)visited = [False] * (n + 1)# 使用优先队列(最小堆)存储待处理的节点,元素为(当前距离, 节点)pq = []# 起点入队,距离为0heapq.heappush(pq, (0, start))# 起点到自身的距离为0minDist[start] = 0# 当优先队列不为空时循环while pq:# 弹出当前距离最小的节点cur_dist, cur_node = heapq.heappop(pq)# 如果节点已被访问,直接跳过if visited[cur_node]:continue# 标记节点为已访问visited[cur_node] = True# 遍历当前节点的所有邻接边for edge in grid[cur_node]:# 如果邻接节点未被访问,且通过当前节点到达邻接节点的距离更短if not visited[edge.to] and cur_dist + edge.val < minDist[edge.to]:# 更新最短距离minDist[edge.to] = cur_dist + edge.val# 将更新后的距离和节点加入优先队列heapq.heappush(pq, (minDist[edge.to], edge.to))# 如果终点不可达,返回-1,否则返回最短距离return -1 if minDist[end] == float('inf') else minDist[end]# 输入部分
# 读取节点总数n和边总数m
n, m = map(int, input().split())
# 读取m条边,每条边格式为"起点 终点 权重"
edges = [tuple(map(int, input().split())) for _ in range(m)]
start = 1 # 设定起点为1
end = n # 设定终点为n# 运行Dijkstra算法并输出结果
result = dijkstra(n, m, edges, start, end)
print(result)Bellman_ford 算法精讲
本题是经典的带负权值的单源最短路问题,此时就轮到Bellman_ford登场了
Bellman_ford算法的核心思想是 对所有边进行松弛n-1次操作(n为节点数量),从而求得目标最短路。
什么是延伸——minDist[B] = min(minDist[A] + value, minDist[B])
按照给出的边的顺序不断循环遍历,对所有边松弛一次 能得到 与起点 一条边相连的节点最短距离。那对所有边松弛两次 可以得到与起点 两条边相连的节点的最短距离。以此延伸(最短边的不断传递)
代码随想录——带负数的最短路劲
代码实现
def main():n, m = map(int, input().strip().split())edges = []for _ in range(m):src, dest, weight = map(int, input().strip().split())edges.append([src, dest, weight])minDist = [float("inf")] * (n + 1)minDist[1] = 0 # 起点处距离为0for i in range(1, n):updated = Falsefor src, dest, weight in edges:if minDist[src] != float("inf") and minDist[src] + weight < minDist[dest]:minDist[dest] = minDist[src] + weightupdated = Trueif not updated: # 若边不再更新,即停止回圈breakif minDist[-1] == float("inf"): # 返还终点权重return "unconnected"return minDist[-1]if __name__ == "__main__":print(main())