双目密集匹配（stereo dense matching）

完全能读懂 👍 这段文字本质上是讲解 双目密集匹配（stereo dense matching）的基本流程、算法分类（局部 vs 全局）、代价函数、SGM半全局匹配原理与改进。

---

一、双目密集匹配基本步骤

1. 基本步骤

1. 代价计算（per-pixel-cost）
2. 代价聚集（cost-aggregation）
3. 视差计算（disparity computation）
4. 视差优化（disparity optimization / refinement）
   

---

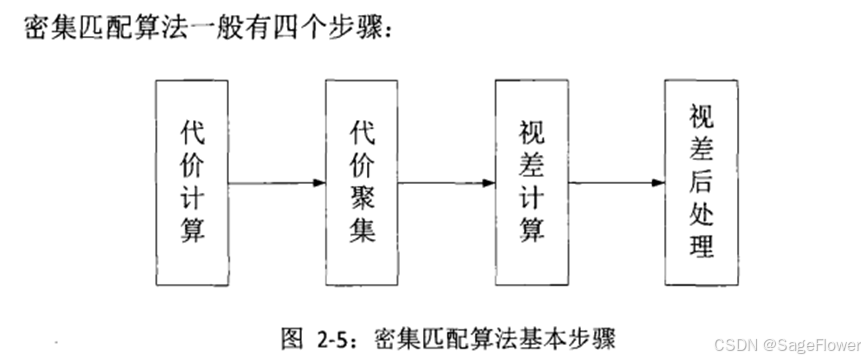
2. 基本步骤含义解释

（1）代价计算（Per-pixel-cost）

• 在给定视差范围内，计算每个像素在不同视差下的代价值。
• 相似度越高，代价越小。

（2）代价聚集（Cost Aggregation）

• 基于窗口或不规则区域的加权平均。

• 在一定邻域范围内，对代价值进行加权或求和，得到新的匹配代价。

• 关键问题：

  • 窗口确定（矩形窗口 vs 自适应不规则窗口）
  • 窗口内加权方式（固定参数 vs 灰度值相关权重）

• 常见算法：
  ASW、SASW、BF、GF、NLC、ST

• WTA 在初始代价空间容易误匹配，但在聚合后的代价上效果显著提升。

（3）视差计算

• 局部算法：WTA 策略，直接选择最小代价值对应的视差。

• 全局算法：通过能量最小化优化累积代价，常见方法：

  • BP
  • MRF
  • GraphCut
  • SGM

（4）视差优化

• 视差结果通常含噪声、误匹配、漏匹配，需要进一步优化。

• 优化方式：

  • 中值滤波
  • 无效区域插值
  • 亚像素精化
  • 一致性检查（LRC）
  • 加权中值滤波（WMF）
  • 小区域移除
    （1）代价计算（per-pixel-cost）：
    Per-pixel-cost, 代价计算是在预先给定的视差范围内，计算出 每个像素 在不同视差值下， 对应的代价值。
    相似度越高，代价越小。
    （2）代价聚集（cost-aggregation）：
    实质是基于窗口或不规则区域的加权平均。
    代价累积是将初始视差空间中的匹配代价在一定的邻域范围内进行求和或加权操作，计算出新的匹配代价，通常采用二维或三维卷积运算。
    代价累积需要考虑两个问题：窗口确定以及窗口内各像素的加权计算方法。
    代价累计窗口可以分为固定的矩形窗口和自适应的不规则窗口；
    加权方法包括两类：一类是有由参数控制的固定权值，一类是根据影像灰度值计算权值。
    常用算法有： ASW（adaptive support weight ），SASW（segment-based adaptive support weight），BF（bilateral filtering），GF（guided filtering），NLC（non-local cost aggregation ），ST（segment tree）
    直接在初始代价值上使用WTA,得到的视差图通常会包含很多错误的结果。在聚集后的代价上使用WTA策略，效果提升是很显著的。
    （3）视差计算：
    视差估计分为局部算法和全局算法。
    局部算法通常直接选择最小的时差最为最优结果，即常见的WTA（winner-take-all）策略。
    全局算法是对视差空间影像在一定邻域范围内进行能量传递，从而计算出累积后的代价。
    全局算法通过建立全局能量函数，将最优视差估计转换为能量最小化问题。常用的全局优化方法包括： BP算法，MRF算法，Graphcut算法，SGM算法。
    （4）视差优化：
    经过上述步骤获取的视差图结果通常会存在一些噪声、误匹配，漏匹配等情况，其次由于大部分立体匹配算法获取的视差都是针对整像素的离散空间中得到，仍需进行拟合获取亚像素级精度。
    通常视差优化操作包括中值滤波，无效区域插值，亚像素级精化等。
    视差后处理（disparity refinement）：不管是全局算法还是局部算法，得到的视差图往往需要视差后处理以提高视差估算精度。
    常用的有： LRC（left-to-right-cross-checking）,中值滤波（MF，median filter），加权中值滤波（WMF, weighted median filter ）, 小区域移除（small area suppress）

---

3. 视差计算的两种方法比较

• 匹配问题可转化为 能量函数优化：

  $$E(D)=\text{Data term}+\text{Smoothness term}$$

• 局部方法：仅包含数据项

• 全局方法：同时包含平滑项，考虑相邻像素约束
  密集匹配问题最后都会转化为能量函数优化问题，能量函数用来度量一幅视差图D的质量。理想的视差图应该具有最小的能量函数值，能量函数有如下形式：
  
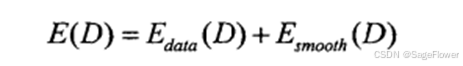
  由数据项和平滑项构成。
  仅包含数据项的匹配方法为局部方法，融合平滑约束的匹配方法为全局方法。

---

二、局部算法和全局算法

1. 局部算法

局部算法是结合代价箱（cost volume）和 WTA 获取视差的方法。
代价函数是一种度量相似性的函数，可分为三种：颜色差异绝对值，基于窗口的度量和互信息。

• 基于代价体（cost volume）+ WTA。

• 常用代价函数：

  • 颜色差异绝对值

    • ADc：绝对色彩差异
    • TADc：截断的绝对色彩差异
    • TADg：截断的梯度差异
    • 常组合颜色差异和梯度差异

  • 基于窗口的度量

    • NCC
    • ZNCC
    • Census

  • 互信息（MI）

2. 全局算法

• 通过能量函数最小化，解决纹理稀疏和视差不连续问题。

• 常见方法：

  1. 动态规划（DP）
  2. Graph Cut（GC）
  3. Belief Propagation（BP）
  4. 基于分割的全局匹配

• 半全局方法（SGM）：将全局优化简化为多路径一维优化，兼顾效率和精度。

---

三、代价函数计算

常见方法：

• SAD（Sum of Absolute Differences）
• SSD（Sum of Squared Differences）
• NCC（Normalized Cross Correlation）
• ZNCC（Zero-mean NCC）
• Census
• MI（Mutual Information）
• BT（Birchfield and Tomasi）

---

四、SGM（半全局匹配算法）详解

0. 概述

• 基于动态规划思想
• 沿 8 或 16 条路径累计代价
• 对能量函数添加 P1、P2 约束项，处理斜面与不连续区域
• 相比全局算法更快，易于 GPU 并行

1. 匹配代价计算

• 常见代价：SAD、Census、MI
• 需要先验视差图

2. 代价聚合

• 通过一维路径聚合代替二维全局优化
• 多路径方向（8 或 16 路）累积

3. 最优代价选择

• 采用 WTA 策略
• 左右一致性检查（LRC）用于去除误匹配和遮挡

4. 能量函数

• 数据项：匹配代价

• 平滑项：相邻像素视差约束

  • P1：小视差变化惩罚（适应斜面）
  • P2：大视差变化惩罚（保留不连续性）

5. 视差优化

• 亚像素精度：二次曲线拟合（抛物线法）
• 后处理：斑块提取、导向滤波、双边滤波
  

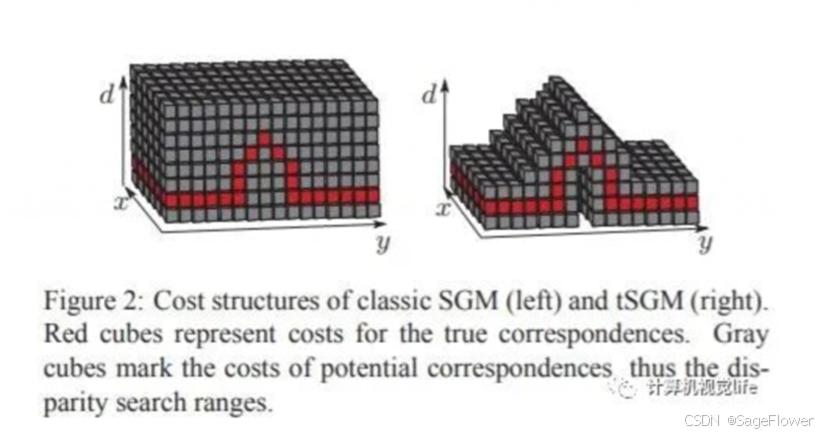
6. 改进方法

• 金字塔层级匹配策略
• tSGM：通过金字塔约束传递视差范围
• 缺点：误差会层层传递

---

五、待解决问题

1. SGM 中互信息计算，256（asp 中的 tile-collar=256）是什么意思？
2. 亚像素精度优化是如何实现的？
3. SGM 中采用 7×7 窗口的高斯平滑处理具体含义？

---