笔试——Day44
文章目录
- 第一题
- 题目
- 思路
- 代码
- 第二题
- 题目
- 思路
- 代码
- 第三题
- 题目
- 思路
- 代码1:动态规划
- 代码2 : 贪心 + 二分
第一题
题目
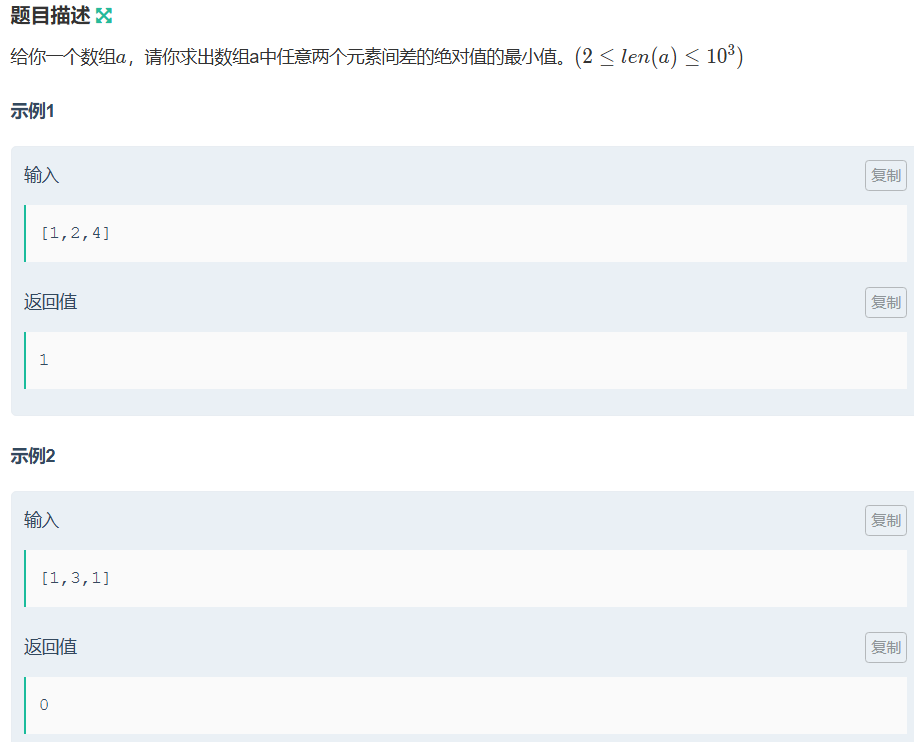
最小差值
思路
排序+遍历
相邻两两比较最小值,注意INT_MAX - INT_MIN 会溢出,使用 long long
代码
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可* 求最小差值* @param a int整型vector 数组a* @return int整型*/int minDifference(vector<int>& a) {// write code heresort(a.begin(), a.end());long long res = a[1] - a[0];for(int i = 2; i < a.size(); i++){res = min(res, (long long)a[i] - a[i - 1]);}return res;}
};
第二题
题目
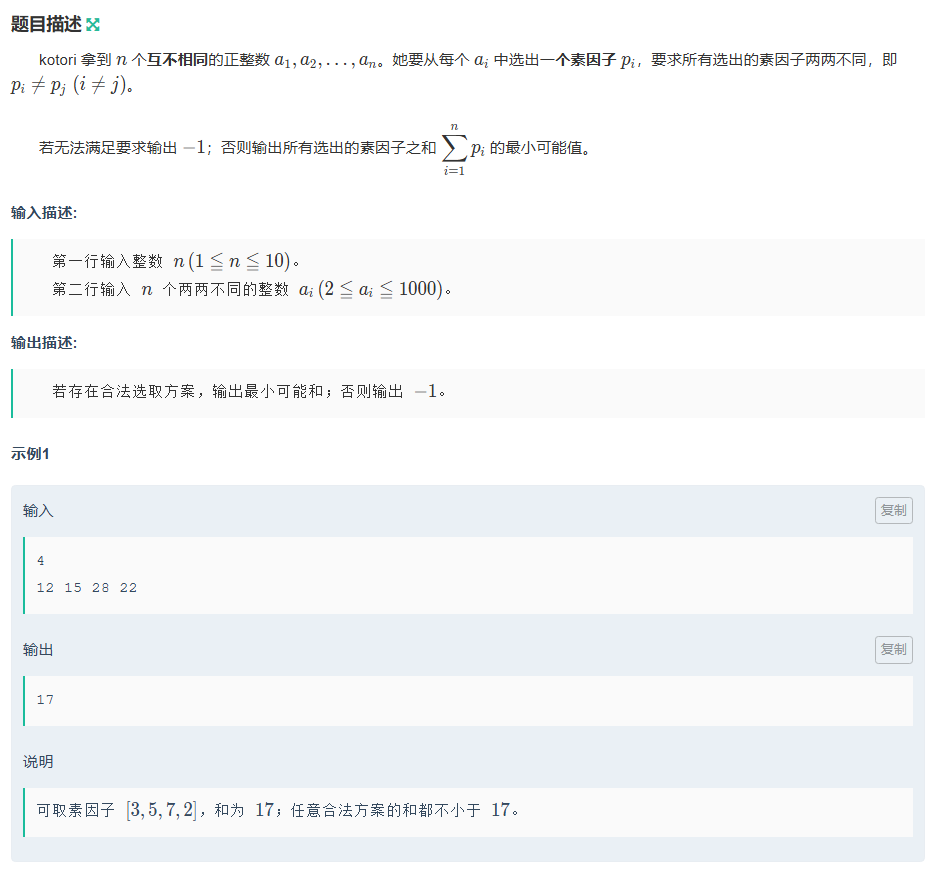
kotori和素因子
思路
DFS
- 每一层可选的数为当前位置的素因子;
代码
// https://ac.nowcoder.com/acm/problem/50042
#include <iostream>
using namespace std;const int N = 11;
const int M = 1010;int n, arr[N];
bool visited[M];
int path;
int res = 0x3f3f3f3f;bool is_prime(int x)
{if(x < 2) return false;for(int i = 2; i * i <= x; i++){if(x % i == 0) return false;}return true;
}void dfs(int pos)
{if(pos == n){res = min(res, path);return ;}for(int i = 2; i <= arr[pos]; i++){if(!visited[i] && is_prime(i) && arr[pos] % i == 0){visited[i] = true;path += i;dfs(pos + 1);path -= i;visited[i] = false;}}
}int main()
{cin >> n;for (int i = 0; i < n; i++){cin >> arr[i];}dfs(0);if(res == 0x3f3f3f3f){cout << "-1" << endl;}else{cout << res << endl;}return 0;
}
第三题
题目
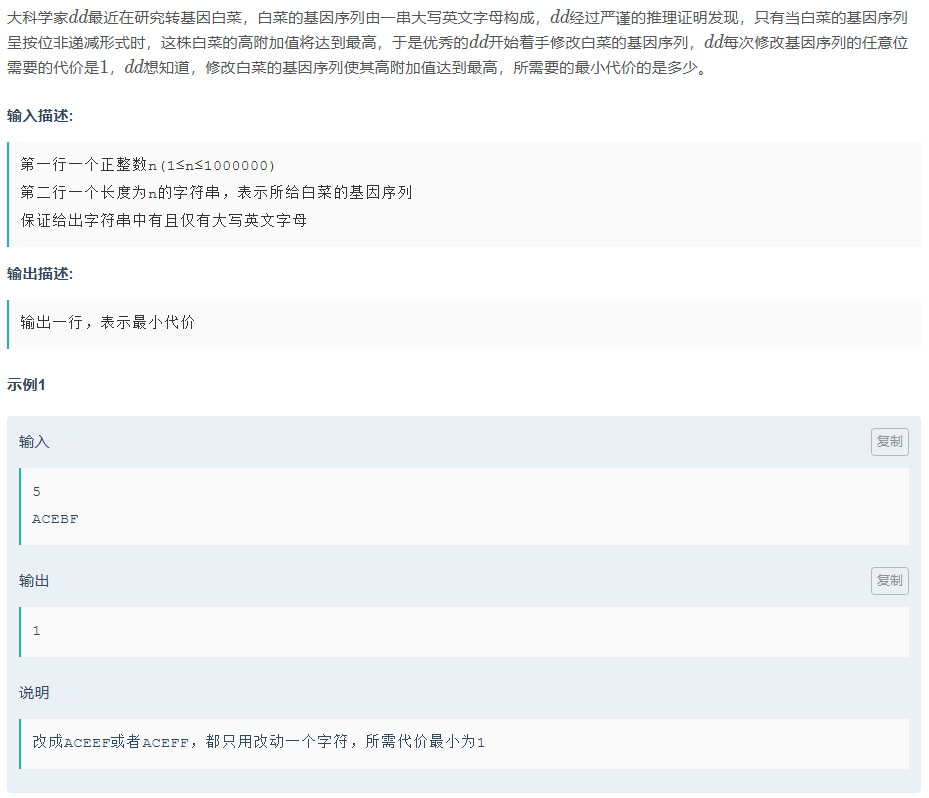
dd爱科学1.0
思路
在最⻓⾮下降⼦序列的基础上,对不是最⻓的部分进⾏更换
- 使用贪心 + 二分;动态规划
O(N^2)会超时
代码1:动态规划
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;const int N = 1e6 + 10;int n;
string s;
int dp[N]; // dp[i] 表示以第i个字符结尾的最长非递减子序列长度int main()
{cin >> n >> s;int max_len = 0;for (int i = 0; i < n; i++) {dp[i] = 1;for (int j = 0; j < i; j++) {if (s[j] <= s[i]) {dp[i] = max(dp[i], dp[j] + 1);}}max_len = max(max_len, dp[i]);}cout << n - max_len << endl;return 0;
}
代码2 : 贪心 + 二分
// https://ac.nowcoder.com/acm/problem/221822
#include <iostream>
#include <string>using namespace std;const int N = 1e6 + 10;int n;
string s;char dp[N]; // 长度为N的的所有子序列中最小的末尾
int res;int main()
{cin >> n >> s;for(int i = 0; i < n; i++){char ch = s[i];// ch 放在哪if(res == 0 || ch >= dp[res]){dp[++res] = ch;}else{// 二分查找int l = 1, r = res;while(l < r){int mid = (l + r) / 2;if(dp[mid] <= ch) l = mid + 1;else r = mid;}dp[l] = ch;}}cout << n - res << endl;return 0;
}