【数据结构】递归与非递归：归并排序全解析

1.归并排序

1.1 递归方式实现归并排序

基本思想：

归并排序的递归实现，核心思想是 “分治 + 合并”—— 将数组不断分割为更小的子数组，待子数组有序后，再将它们合并为更大的有序数组。

归并排序核心步骤：

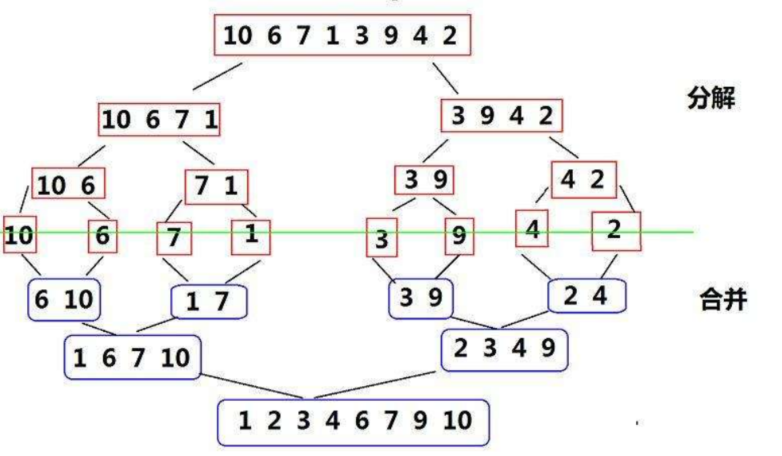
归并排序的单趟思想就是合并两个有序数组；

把数组拆成两半 → 递归拆到最小（单个元素）→ 逐层合并成有序数组

代码分步拆解

1. MergeSort（外层）：

   1. 申请临时数组 tmp（合并时用，避免覆盖原数据）

   2. 调用 _MergeSort 处理整个数组 [0, n-1]

   3. 用完释放 tmp

2. _MergeSort（递归核心）：

   1. 终止条件：left >= right（数组只剩 1 个元素，天然有序，直接返回）

   2. 分：算中间位置 mid，递归拆分左 [left, mid]、右 [mid+1, right]

   3. 治（合并）：

      a.用双指针遍历左右有序子数组，按小到大存到 tmp                           b.处理剩余元素（某子数组遍历完，把另一数组剩下的直接搬过去）                              c.把 tmp 里合并好的结果，拷回原数组 a

   4. void MergeArr(int* a, int begin1, int end1, int begin2, int end2, int* tmp)
      {int left = begin1, right = end2;int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}while (begin1 <= end1)tmp[index++] = a[begin1++];while (begin2 <= end2)tmp[index++] = a[begin2++];//把归并好的tmp的数据再拷贝会原数组for (int i = left; i <= right; i++){a[i] = tmp[i];}
      }void _MergeSort(int* a, int left, int right, int* tmp)
      {if (left >= right)return;int mid = (left + right) / 2;//[left,mid][mid+1,right]有序，则可以合并，现在他们没有序，子问题解决_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);//归并[left,mid][mid+1,right]有序MergeArr(a, left, mid, mid + 1, right, tmp);
      }// 归并排序递归实现 
      void MergeSort(int* a, int n)
      {assert(&a);int* tmp = malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);
      }

      归并排序特点：

      1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。

      2. 时间复杂度：O(N*logN)

      3. 空间复杂度：O(N)

      4. 稳定性：稳定

1.2非递归方式实现归并排序

//将[begin1, end1]和[begin2, end2]两个有序子数组合并为一个有序数组，结果存回原数组
/*
① 双指针遍历两个子数组，每次取较小元素放入临时数组tmp；
② 处理剩余元素（某一子数组先遍历完时，直接拷贝剩余元素到tmp）；
③ 将tmp中合并好的结果拷贝回原数组a的对应区间[left, right]。
*/
void MergeArr(int* a, int begin1, int end1, int begin2, int end2, int* tmp)
{int left = begin1, right = end2;int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}while (begin1 <= end1)tmp[index++] = a[begin1++];while (begin2 <= end2)tmp[index++] = a[begin2++];//把归并好的tmp的数据再拷贝会原数组for (int i = left; i <= right; i++){a[i] = tmp[i];}
}// 归并排序非递归实现 
/*
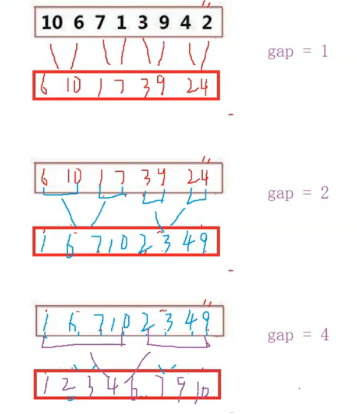
① 初始gap=1（最小子数组长度），每次循环后gap翻倍（gap *= 2）；
② 每次循环中，按2*gap的间隔遍历数组，将[i, i+gap-1]和[i+gap, i+2*gap-1]两个子数组合并；
③ 重复上述过程，直到gap超过数组长度（此时已合并为完整的有序数组）。
*/
// 归并排序非递归实现 
void MergeSortNonR(int* a, int n)
{assert(a);int* tmp = malloc(sizeof(int) * n);int gap = 1;while (gap < n ){for (int i = 0; i < n; i += 2 * gap){// 确定两个待合并子数组的边界int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;//1.合并时只有第一组，第二组不存在，就不需要合并if (begin2 >= n)break;//2.合并时第二组只有部分数据，需要修正end的边界if (end2 >= n)end2 = n - 1;//[i,i+gap-1] [i+gap,i+2*gap-1]MergeArr(a, begin1, end1, begin2, end2, tmp);}gap *= 2;}free(tmp);
}

步长增长：gap从 1 开始，每次翻倍（1→2→4→...），控制合并的子数组大小。

子数组划分：每个循环中，子数组按[i, i+gap-1]和[i+gap, i+2*gap-1]划分，两两合并。

依赖MergeArr：合并逻辑封装在MergeArr中，负责具体的双指针合并和数据拷贝。