算法提升树形数据结构-(线段树)
今天介绍有关线段树的相关部分的知识,线段树是树的数据结构中十分重要的算法处理思想。

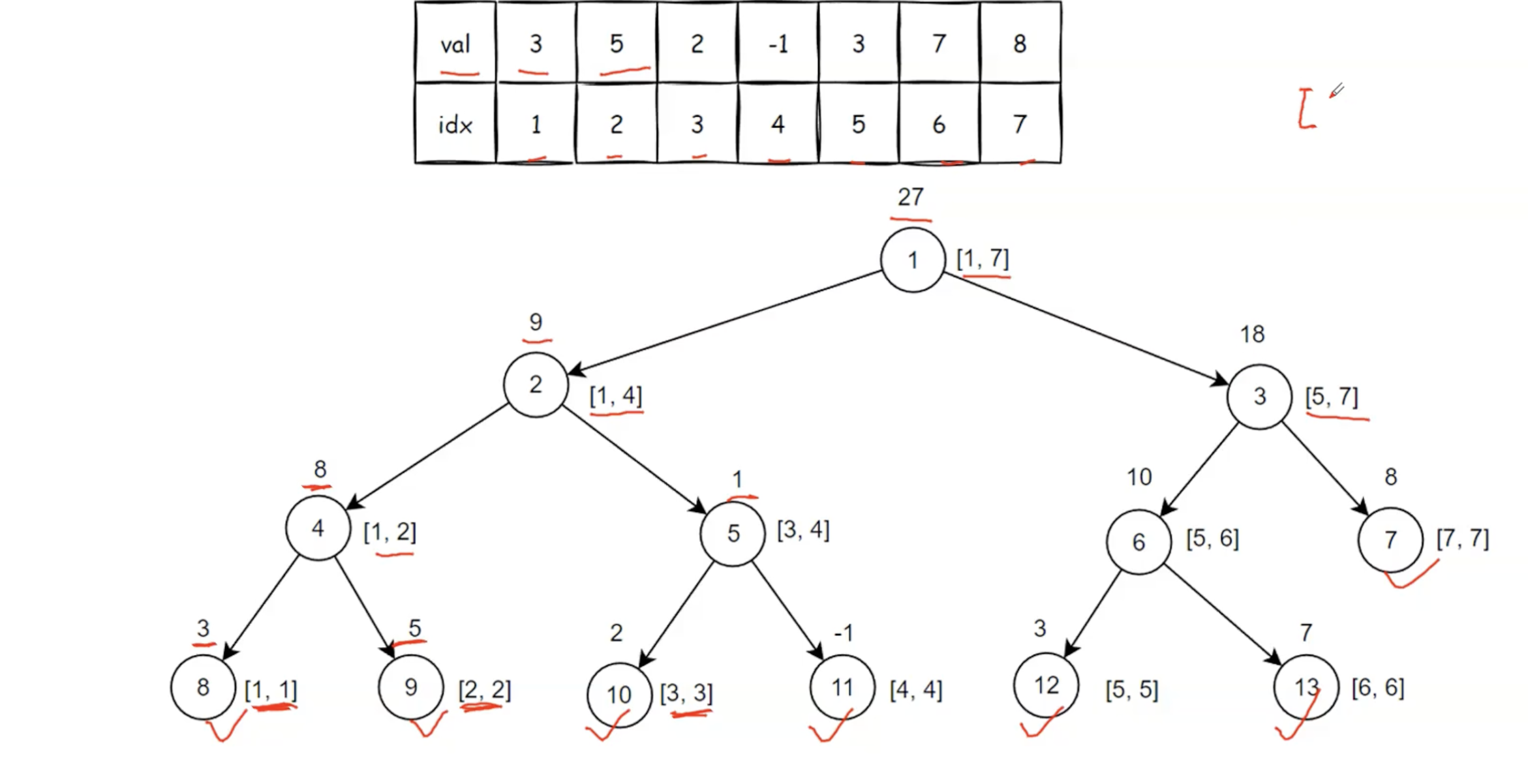
1.建立初始树的条件

2.基本框架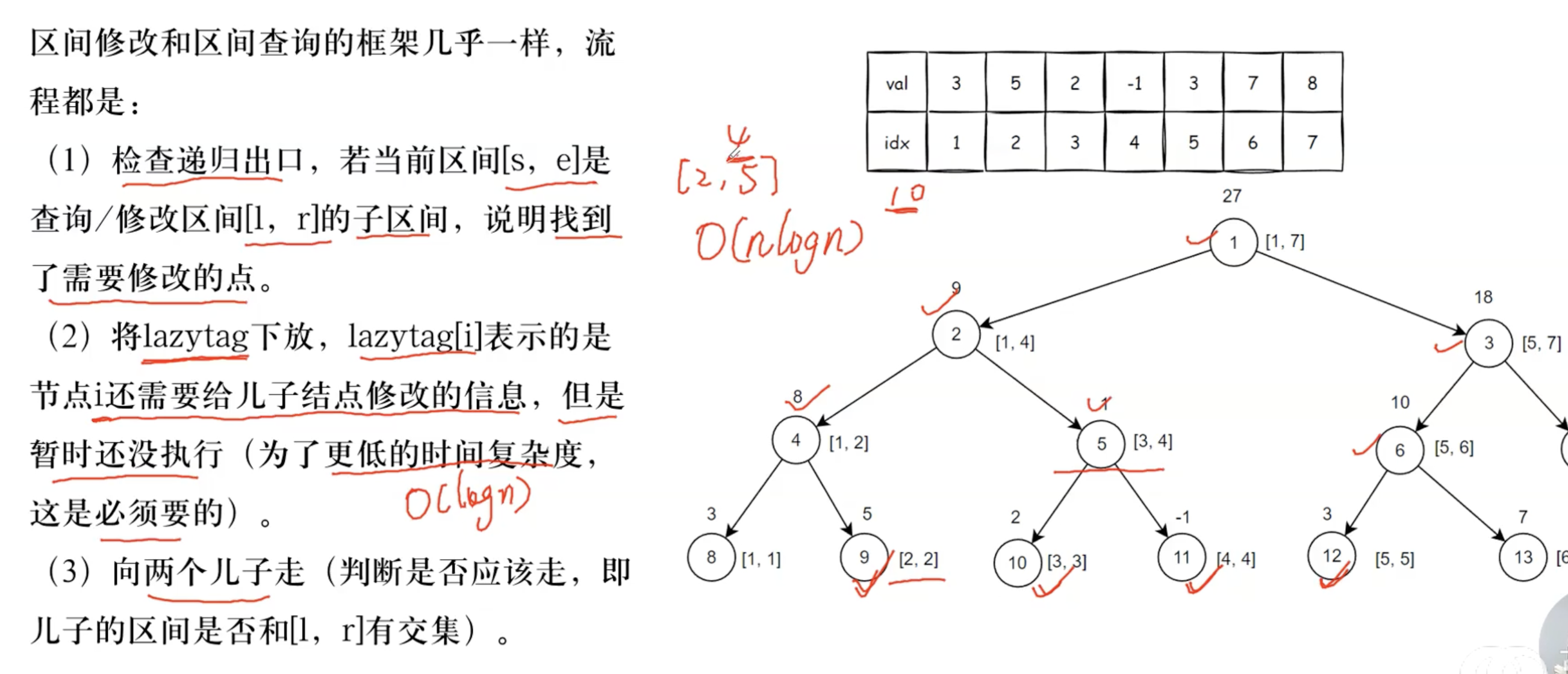
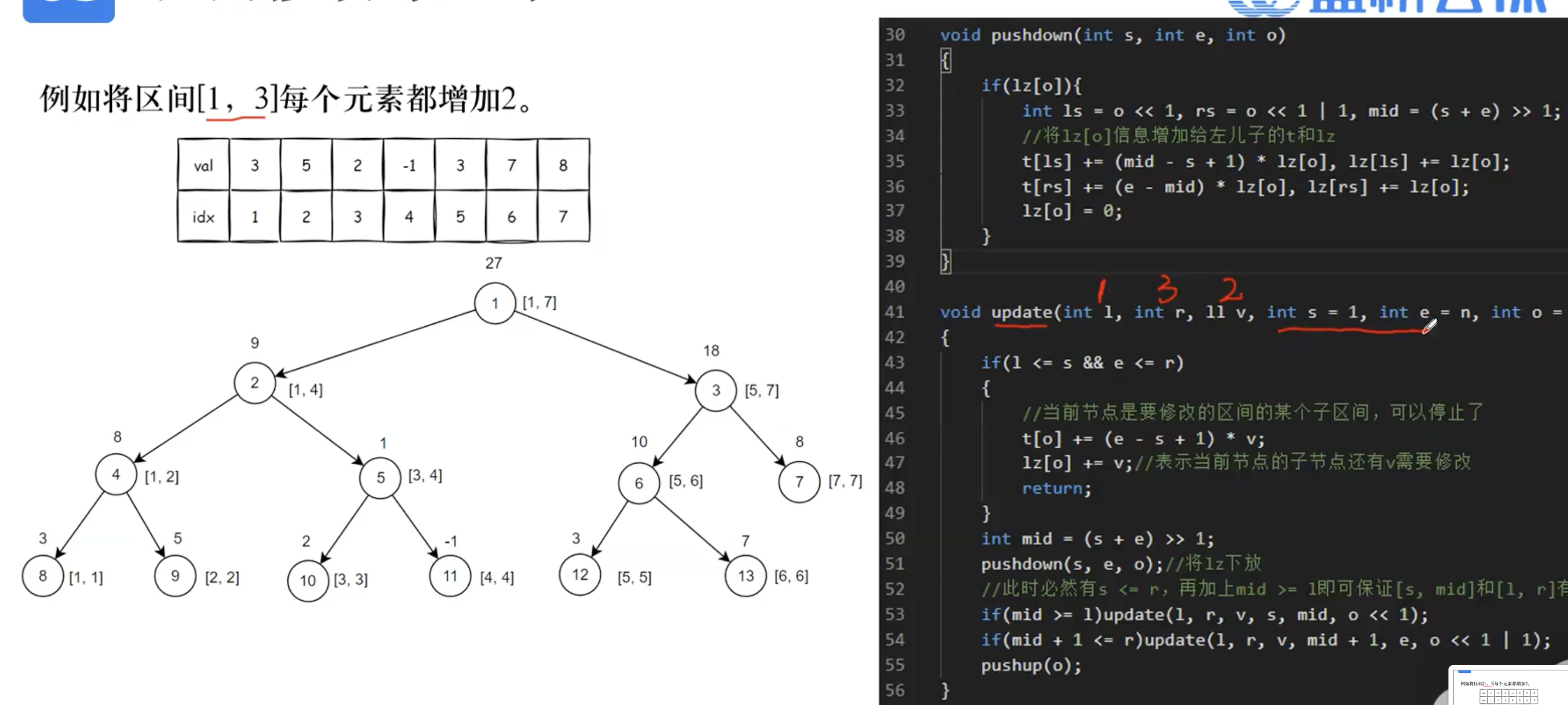
3.区间修改的相关代码
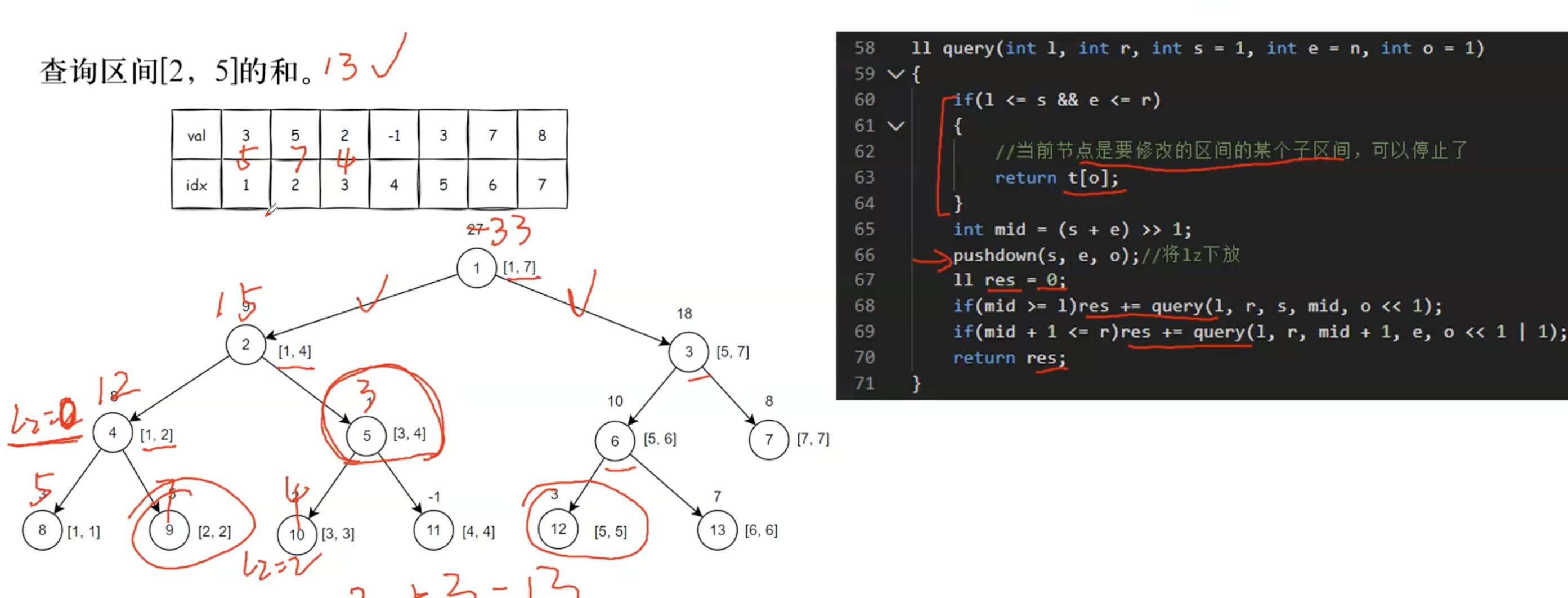
4.区间查询的代码
题目描述
给定一个长度为 N 的数组 a,其初值分别为 a1,a2,...,aN。
现有 Q 个操作,操作有以下两种:
1 l r k,将区间 al,al+1,...ar 的值加上 k。2 l r,求区间 al,al+1,...,aral 的和为多少。
输入描述
输入第 1行包含两个正整数 N,Q,分别表示数组 a 的长度和操作的个数。
第 2 行包含 N 个非负整数 a1,a2,...,aN,表示数组 a 元素的初值。
第 3∼Q−2 行每行表示一共操作,格式为以下两种之一:
1 l r x2 l r
其含义如题所述。
1≤N,Q≤105,1≤l≤r≤N,−109≤k,ai≤109。
输出描述
输出共 Q行,每行包含一个整数,表示相应查询的答案。
输入输出样例
5 5
1 2 3 4 5
2 1 2
1 2 3 1
2 1 3
1 1 5 1
2 1 5
3
8
22代码部分:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;const int N = 1e5+5;
int n;
int a[N];
ll t[4*N],lz[4*N];void pushup(int o){t[o]=t[o<<1]+t[o<<1|1];
}
void pushdown(int s,int e,int o){if(lz[o]){int ls=o<<1,rs=o<<1|1;int mid=s+e>>1;t[ls]+=(mid-s+1)*lz[o],lz[ls]+=lz[o];t[rs]+=(e-mid)*lz[o],lz[rs]+=lz[o];lz[o]=0; }
}
void build(int s=1,int e=n,int o=1){if(s==e){t[o]=a[s];return;}int mid=s+e>>1;build(s,mid,o<<1);build(mid+1,e,o<<1|1);pushup(o);
}
void update(int l,int r,ll v,int s=1,int e=n,int o=1){if(s>=l&&e<=r){lz[o]+=v;t[o]+=(e-s+1)*v;return;}int mid=s+e>>1;pushdown(s,e,o);if(mid>=l) update(l,r,v,s,mid,o<<1);if(mid+1<=r) update(l,r,v,mid+1,e,o<<1|1);pushup(o);
}
ll query(int l,int r,int s=1,int e=n,int o=1){if(s>=l&&e<=r){return t[o];}int mid=s+e>>1;pushdown(s,e,o);ll res=0;if(mid>=l) res+=query(l,r,s,mid,o<<1);if(mid+1<=r) res+=query(l,r,mid+1,e,o<<1|1);return res;
}void solve() {int op;cin>>op;if(op==1){int l,r,v;cin>>l>>r>>v;update(l,r,v);}else{int l,r;cin>>l>>r;cout<<query(l,r)<<endl;}
}
int main() {ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;int q;cin>>q;for(int i=1;i<=n;i++) cin>>a[i];build(); while(q--) {solve();}return 0;
}问题描述
给定一个长度为 N 的数列 A1,A2,⋯,AN 。现在小蓝想通过若干次操作将 这个数列中每个数字清零。
每次操作小蓝可以选择以下两种之一:
- 选择一个大于 0 的整数, 将它减去 1 ;
- 选择连续 K 个大于 0 的整数, 将它们各减去 1 。
小蓝最少经过几次操作可以将整个数列清零?
输入格式
输入第一行包含两个整数 N 和 K 。
第二行包含 N 个整数 A1,A2,⋯,AN 。
输出格式
输出一个整数表示答案。
输入案例:
4 2
1 2 3 4输出案例:
6代码部分:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
ll lz[N * 4], t[N * 4], a[N], n, k, ans;void pushup(ll o)
{t[o] = min(t[o << 1], t[o << 1 | 1]);
}void build(ll s = 1, ll e = n, ll o = 1)
{if (s == e){t[o] = a[s];return;}ll mid = s + e >> 1;build(s, mid, o << 1);build(mid + 1, e, o << 1 | 1);pushup(o);
}void pushdown(ll s, ll e, ll o)
{if (lz[o]){ll ls = o << 1, rs = o << 1 | 1, mid = s + e >> 1;t[ls] -= lz[o], lz[ls] += lz[o];t[rs] -= lz[o], lz[rs] += lz[o];lz[o] = 0;}
}void update(ll l, ll r, ll v, ll s = 1, ll e = n, ll o = 1)
{if (l <= s && e <= r){t[o] -= v;lz[o] += v;return;}ll mid = s + e >> 1;pushdown(s, e, o);if (mid >= l)update(l, r, v, s, mid, o << 1);if (mid + 1 <= r)update(l, r, v, mid + 1, e, o << 1 | 1);pushup(o);
}ll query(ll l, ll r, ll s = 1, ll e = n, ll o = 1)
{if (l <= s && e <= r)return t[o];ll mid = s + e >> 1;pushdown(s, e, o);ll res = 1e9;if (mid >= l)res = min(res, query(l, r, s, mid, o << 1));if (mid + 1 <= r)res = min(res, query(l, r, mid + 1, e, o << 1 | 1));return res;
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> n >> k;for (ll i = 1; i <= n; ++i)cin >> a[i];build();for (ll i = 1; i <= n; ++i){if (i + k - 1 <= n) // 还可以执行k操作{// 询问得到最小值ll x = query(i, i + k - 1);if (x != 0){ans += x;update(i, i + k - 1, x);}}ll y = query(i, i);if (y != 0){ans += y;update(i, i, y);}}cout << ans;
}update(i, i + k - 1, x),可以直接减去x,这样就可以提高效率。
今天的分享就到这里,关于线段树的内容是算法比赛中经常考察的部分,希望大家能有所收获。
