【递归、搜索与回溯算法】记忆化搜索

- 记忆化搜索简介
- 1. 记忆化是什么
- 2. 如何实现记忆化搜索
- 3. 动态规划 vs 记忆化搜索
- 4. 问题
- 一、[斐波那契数](https://leetcode.cn/problems/fibonacci-number/description/)
- 二、[不同路径](https://leetcode.cn/problems/unique-paths/description/)
- 三、[最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/description/)
- 四、[猜数字大小 II](https://leetcode.cn/problems/guess-number-higher-or-lower-ii/description/)
- 五、[矩阵中的最长递增路径](https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/description/)
- 结尾
记忆化搜索简介
1. 记忆化是什么
记忆化搜索是一种优化递归算法的技术,通过存储已计算的子问题结果来避免重复计算,从而显著提高效率。
记忆化搜索本质上就是带了备忘录的递归,假设在递归的过程中,在出现大量相同问题的,记忆化搜索能够极大提高效率。
以求斐波那契数为例,看下图,使用递归求斐波那契数时,存在大量的相同问题,假设如果在递归的过程中,记录相同问题的结果,那么就可以减少很多没必要的递归。
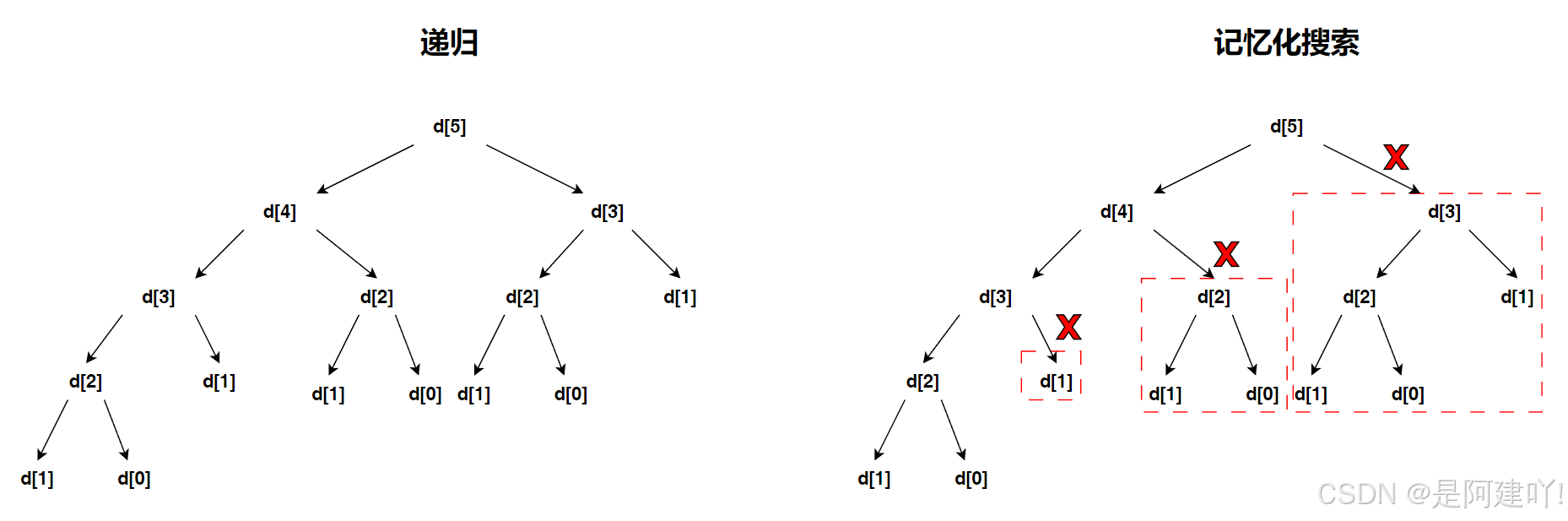
2. 如何实现记忆化搜索
- 添加一个备忘录(<可变参数,返回值>)
- 递归每次返回的时候,将结果放入到备忘录中
- 在每次进入递归的时候,查看备忘录中是否可以直接获取结果
3. 动态规划 vs 记忆化搜索
动态规划的步骤与记忆化搜索的步骤可以一 一对应:
| 动态规划 | 核心含义 | 记忆化搜索 | 核心含义 |
|---|---|---|---|
| 1. 确认状态表示 | 定义 dp[i] 或 dp[i][j] 表示某个状态的含义(如 dp[i] 表示前 i 个元素的最优解) | dfs 函数的含义 | dfs(i) 函数的返回值直接对应 dp[i] 的含义 |
| 2. 推导递归转移方程 | 通过数学公式描述状态之间的递推关系 | dfs 的函数体 | dfs(i) 的函数体直接实现这个递推关系 |
| 3. 初始化 | 设定最小子问题的解 | dfs 函数的递归出口 | 定义递归终止条件,直接返回最小子问题的解 |
| 4. 确定填写顺序 | 按子问题依赖关系确定计算顺序 | 填写备忘录顺序 | 递归过程中自然按 “自顶向下” 顺序计算子问题,备忘录随递归调用自动填充,无需手动规划顺序 |
| 5. 确认返回值 | 最终结果对应 dp 表的某个状态 | 主函数数如何调用 dfs 函数的 | 主函数调用对应原问题的 dfs 参数,直接获取原问题的解 |
4. 问题
- 问:所有的递归(暴搜、深搜),都能改成记忆化搜索嘛?
答:不是,只有在递归过程中,出现大量相同的问题时,才能使用记忆化搜索进行优化 - 问:带备忘录的递归 vs 带备忘录的动态规划 vs 记忆化搜索
答:本质上都是一回事
一、斐波那契数
题目描述:

思路讲解:
本道题需要我们计算斐波那契数,斐波那契数的定义为 F(n) = F(n-1) + F(n-2)(n>1),基础项为 F(0)=0、F(1)=1,通过定义我们发现了重复子问题,所以本道题可以使用递归,但是直接递归会产生大量重复计算,因此采用记忆化搜索优化。以下是具体思路:

- 全局变量:
- memory:记忆化表,其中 memory[i] 存储第 i 个斐波那契数的值。初始化为 -1 表示该位置尚未计算,计算后更新为对应值
- 递归逻辑:
- 递归出口:
- 当 n=0 或 n=1 时,直接返回 n,并将结果存入 memory
- 记忆化查询与计算:
- 调用 dfs(n) 时,先检查 memory[n]:
- 若 memory[n] != -1(已计算),直接返回存储的结果,避免重复递归
- 若未计算,则根据递推关系 F(n) = F(n-1) + F(n-2),递归调用 dfs(n-1) 和 dfs(n-2),计算结果后存入 memory[n] 并返回
- 递归出口:
编写代码:
// 递归
class Solution {
public:int dfs(int n){if(n == 0 || n == 1) return n;return dfs(n-1) + dfs(n-2);}int fib(int n) {return dfs(n);}
};// 记忆化搜索
class Solution {vector<int> memory;
public:int dfs(int n){if(memory[n] != -1){return memory[n];}if(n == 0 || n == 1) {memory[n] = n;return n;}memory[n] = dfs(n-1) + dfs(n-2);return memory[n];}int fib(int n) {memory = vector<int>(n+1,-1);return dfs(n);}
};// 动态规划
class Solution {
public:int fib(int n) {vector<int> memory(n + 2,-1);memory[0] = 0 , memory[1] = 1;for(int i = 2 ; i <= n ; i++){memory[i] = memory[i-1] + memory[i-2];}return memory[n];}
};
二、不同路径
题目描述:
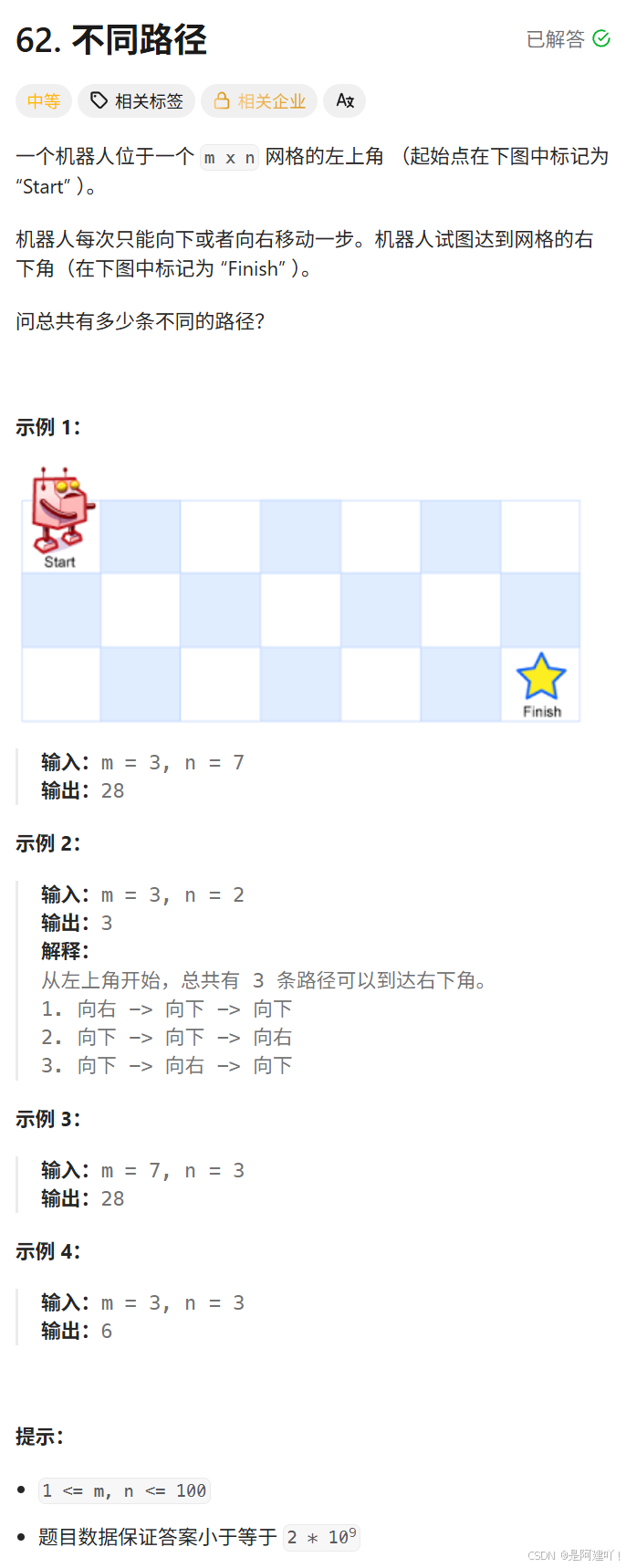
思路讲解:
本道题需要我们找到机器人在网格中从左上角到右下角中所有的路径,机器人每次只能向下或者向右移动一步。问题可拆解为:以下图为例,到达(i,j)的路径条数就等于到达(i-1,j)的路径 + 到达(i,j-1)的路径。发现了重复子问题,我们可以通过递归探索机器人从左上角到右下角的所有可能路径,但是直接递归会有大量重复计算,所以这里我们使用记忆化搜索进行优化。以下是具体思路:
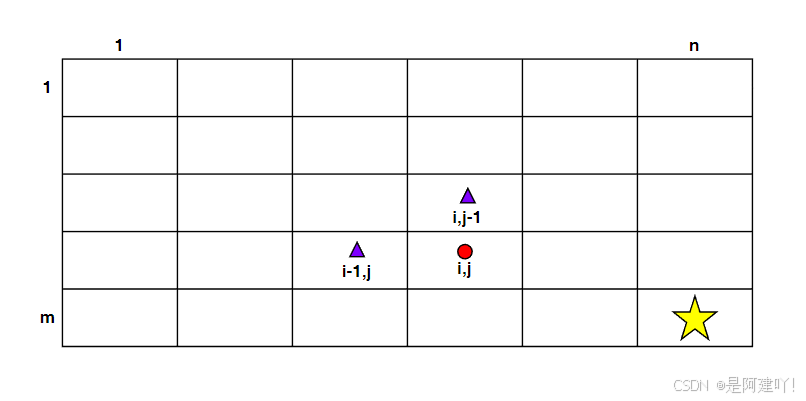
- 全局变量:
- memory:记忆化表,其中 memory[row][col] 存储到达(row, col)的路径数。初始化为 -1 表示该位置尚未计算,计算后更新为对应路径数
- 递归逻辑:
- 调用 dfs(row, col) 时,先检查 memory[row][col],若不为0(已计算),直接返回存储的结果,避免重复递归
- 递归出口(边界条件):
- 当 row == 0 或 col == 0 时(超出网格范围,非有效坐标),返回 0(无路径可达)
- 当 row == 1 && col == 1 时(起点),路径数为 1(只有一种方式停在起点),存入记忆化表后返回 1
- 对于其他有效坐标(row, col),路径数为左侧路径数与上侧路径数之和,即 memory[row][col] = dfs(row, col-1) + dfs(row-1, col),计算后返回结果
- 整体流程:
- 初始化记忆化表 memory 为 (m+1) x (n+1) 的二维向量,全部设为 -1(适配 1-based 索引,避免处理 0 行 0 列的边界问题)
- 调用 dfs(m, n) 启动递归计算,最终返回 dfs(m, n) 的结果
编写代码:
class Solution {vector<vector<int>> memory;
public:int dfs(int row , int col){if(memory[row][col] != 0){return memory[row][col];}if(row == 0 || col == 0){return 0;}if(row == 1 && col == 1){memory[row][col] = 1;return 1;}memory[row][col] = dfs(row,col-1) + dfs(row-1,col);return memory[row][col];} int uniquePaths(int m, int n) {memory = vector<vector<int>>(m+1,vector<int>(n+1,0));return dfs(m,n);}
};
三、最长递增子序列
题目描述:

思路讲解:
本道题需要我们找到最长递增子序列,我们通过递归探索以数组每个位置为起点的最长严格递增子序列长度,但是直接递归会有大量重复计算,这里使用记忆化搜索进行优化。以下是具体思路:
- 全局变量:
- memory:记忆化表,其中 memory[pos] 存储以第pos个元素为起点的最长严格递增子序列长度。初始化为 -1 表示该位置尚未计算,计算后更新为对应长度
- 递归逻辑:
- 调用 dfs(nums, pos) 时,先检查 memory[pos],若不为 -1(已计算),直接返回存储的结果,避免重复递归
- pos为起点的最小长度为 1(仅包含自身),因此初始值 ret = 1
- 遍历pos右侧的所有元素:
- 若 nums[i] > nums[pos],则以pos为起点的长度可更新为 max(ret, dfs(nums, i) + 1)
- 将计算得到的ret存入 memory[pos] 并返回
- 整体流程:
- 初始化记忆化表 memory 为与数组nums同长度的向量,全部设为 -1
- 遍历数组每个位置i,调用 dfs(nums, i) 计算以i为起点的最长递增子序列长度
- 记录所有起点的最长递增子序列长度的最大值 ans,作为整个数组的最长递增子序列长度返回
编写代码:
class Solution {vector<int> memory;
public:int dfs(vector<int>& nums , int pos){if(memory[pos] != -1){return memory[pos];}int ret = 1;for(int i = pos + 1 ; i < nums.size() ; i++){if(nums[i] > nums[pos]){ret = max(ret,dfs(nums,i)+1);}}memory[pos] = ret;return memory[pos];}int lengthOfLIS(vector<int>& nums) {memory = vector<int>(nums.size(),-1);int ans = 0;for(int i = 0 ; i < nums.size() ; i++){ans = max(ans,dfs(nums,i));}return ans;}
};
四、猜数字大小 II
题目描述:

思路讲解:
本道题要求我们从从 1 到 n 中猜一个数字,猜错时需支付所猜数字的金额,目标是找到确保获胜的最小现金数(即无论论对方选哪个数字,都能猜对且花费最少)。问题可拆解为:在数字范围 [left, right] 中猜数的最小成本,取决于选择中间某个数字 i 作为猜测值时的最大风险成本(左区间或右区间的最大成本)加上 i 的金额,再取所有可能 i 中的最小值。发现重复子问题,这道题可以使用递归完成,但是直接递归会产生大量重复计算,所以这里使用记忆化搜索进行优化,以下是具体思路:
- 全局变量:
- memory:记忆化表,其中 memory[left][right] 存储范围 [left, right] 的最小确保获胜成本。初始化为 -1 表示该范围尚未计算,计算后更新为对应成本
- 递归逻辑:
- 当 left >= right 时,无需猜测成本,返回 0
- 调用 dfs(left, right) 时,先检查 memory[left][right],若不为 -1,直接返回存储的结果,避免重复递归
- 遍历区间 [left, right] 中的每个数字 i,假设猜测 i:
- 若猜错,需支付 i 的金额,并进入左区间 [left, i-1] 或右区间 [i+1, right] 继续猜数,取两个区间中成本较大的那个
- 计算猜测 i 的总成本为 max(dfs(left, i-1), dfs(i+1, right)) + i
- 在所有可能的 i 中取总成本的最小值,作为当前区间 [left, right] 的最小确保获胜成本,即 ret = min(ret, 上述总成本)
- 存储结果:将计算得到的ret存入 memory[left][right] 并返回
- 整体流程:
- 初始化记忆化表 memory 为 (n+1) x (n+1) 的二维向量,全部设为 -1
- 调用 dfs(1, n) 启动递归计算,最终返回 dfs(1, n) 的结果,即从 1 到 n 范围中确保获胜的最小现金数
编写代码:
class Solution {vector<vector<int>> memory;
public:int dfs(int left , int right){if(left >= right) return 0;if(memory[left][right] != -1){return memory[left][right];}int ret = INT_MAX;for(int i = left; i <= right ; i++){int tmp = max(dfs(left,i-1),dfs(i+1,right)) + i;ret = min(tmp,ret);}memory[left][right] = ret;return ret;}int getMoneyAmount(int n) {memory = vector<vector<int>>(n+1,vector<int>(n+1,-1));return dfs(1,n); }
};
五、矩阵中的最长递增路径
题目描述:
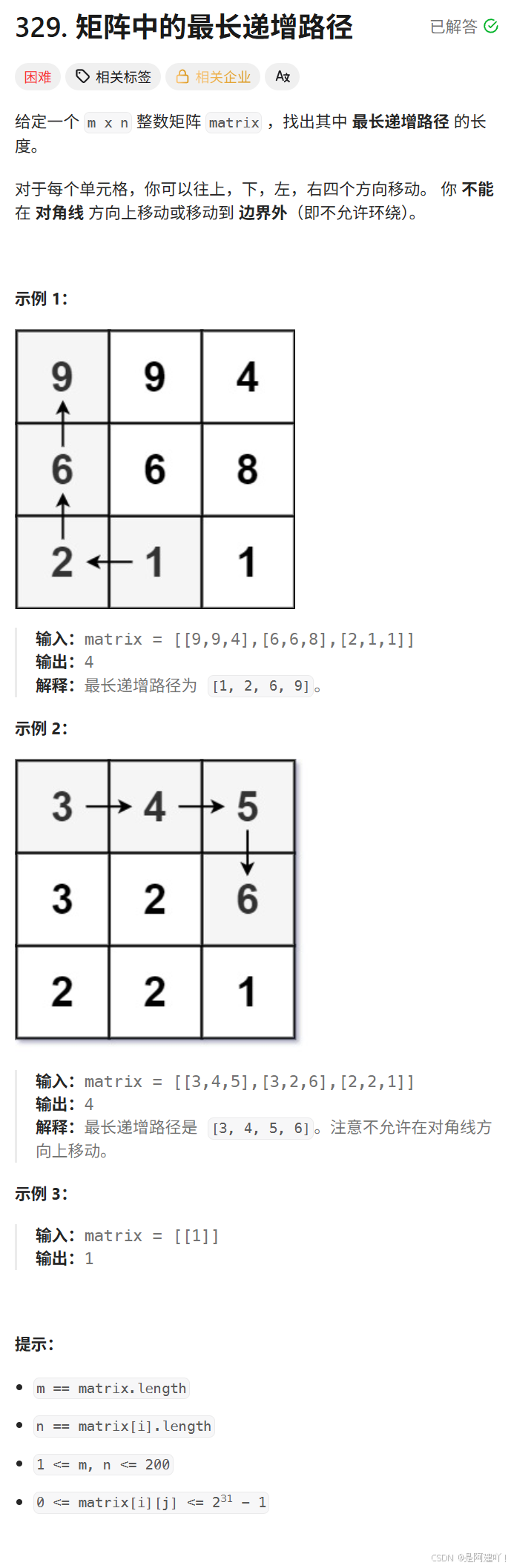
思路讲解:
本道题需要我们找到矩阵中的最长递增路径,最长递增路径是指从矩阵某单元格出发,向上下左右四个方向移动,每次只能到值更大的单元格,形成的路径中最长的那条。问题可拆解为:以单元格(row, col)为起点的最长递增路径长度,等于其四个方向上所有值更大的相邻单元格的最长路径长度的最大值加 1。发现重复子问题,这道题可以使用递归完成,但是直接递归会产生大量重复计算,所以这里使用记忆化搜索进行优化,以下是具体思路:
- 全局变量:
- memory:存储每个单元格的最长递增路径长度,memory[row][col] 表示以(row, col)为起点的最长路径长度,初始化为 -1 表示未计算
- dx , dy:方向数组,表示上下左右四个方向的坐标偏移
- vis:标记当前路径中的单元格
递归逻辑: - 调用 dfs(matrix, row, col) 时,先检查 memory[row][col],若不为 -1(已计算),直接返回存储的结果,避免重复递归
- 遍历四个方向,计算相邻单元格,检查其合法性:
- 坐标在矩阵边界内
- 相邻单元格值大于当前单元格值
- 未被当前路径访问
- 对符合条件的相邻单元格,递归计算其最长路径长度,并取最大值 ret。当前单元格的最长路径长度为 ret + 1(加 1 表示包含自身)
- 将计算得到的长度存入 memory[row][col] 并返回
- 整体流程:
- 初始化矩阵尺寸 rows 和 cols,以及 vis 数组和 memory 记忆化表
- 遍历矩阵每个单元格 (i, j),调用 dfs(matrix, i, j) 计算以其为起点的最长递增路径长度
- 记录所有起点的路径长度的最大值 ans,并返回
编写代码:
class Solution {int dx[4] = {0,0,-1,1};int dy[4] = {1,-1,0,0};int rows , cols;vector<vector<bool>> vis;vector<vector<int>> memory;
public:int dfs(vector<vector<int>>& matrix , int row , int col){if(memory[row][col] != -1){return memory[row][col];}int ret = 0;for(int i = 0 ; i < 4 ; i++){int x = row + dx[i] , y = col + dy[i];if(0 <= x && x < rows && 0 <= y && y < cols && matrix[x][y] > matrix[row][col] && vis[x][y] == false){ret = max(dfs(matrix,x,y),ret);}}memory[row][col] = ret + 1;return ret + 1;}int longestIncreasingPath(vector<vector<int>>& matrix) {rows = matrix.size() , cols = matrix[0].size();vis = vector<vector<bool>>(rows,vector<bool>(cols,false));memory = vector<vector<int>>(rows,vector<int>(cols,-1));int ans = 0;for(int i = 0 ; i < rows ; i++){for(int j = 0 ; j < cols ; j++){ans = max(ans,dfs(matrix,i,j));}}return ans;}
};
结尾
如果有什么建议和疑问,或是有什么错误,大家可以在评论区中提出。
希望大家以后也能和我一起进步!!🌹🌹
如果这篇文章对你有用的话,希望大家给一个三连支持一下!!🌹🌹

