机器学习——PCA算法
主成分分析（PCA, Principal Component Analysis）是机器学习中常用的无监督降维算法，其核心思想是通过线性变换将高维数据投影到低维空间，同时保留最大方差信息。以下是PCA的关键步骤和原理总结：
1. PCA的核心思想
•目标：
PCA（Principal Component Analysis，主成分分析）的主要目标是通过线性变换，将原始高维数据投影到一个更低维的空间中，同时尽可能保留数据的主要特征。这些主要特征通常表现为数据中方差最大的方向，因为方差大的方向往往蕴含更多的信息量。
例如，在图像处理中，一张1000×1000像素的图片可以看作是一个100万维的数据点。利用PCA，我们可以将其压缩到几十或几百个维度，同时依然保留图像的主要结构和特征。
•PCA的数学基础是协方差矩阵的特征值分解，具体步骤如下：
- 数据标准化：将原始数据按特征进行中心化（减去均值）和标准化（可选），使每个特征的均值为0，方差为1（如果数据尺度差异较大）。
- 计算协方差矩阵：协方差矩阵反映了数据不同特征之间的线性相关性。
- 特征值分解：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。特征值的大小表示对应特征向量方向上的方差贡献。
- 选择主成分：按照特征值从大到小排序，选取前k个最大的特征值对应的特征向量，构成新的低维空间。
- 数据投影：将原始数据投影到选定的k个主成分上，得到降维后的数据。
例如，假设我们有一个二维数据集，协方差矩阵的特征值分别为3和1，对应的特征向量分别为[1, 1]和[-1, 1]。如果我们希望降至一维，则选择特征值3对应的特征向量[1, 1]作为主成分方向，将数据投影到该方向上。
2. PCA算法步骤
1. 数据准备
假设原始数据矩阵 X 为 n×d 维（n 个样本，d 个特征），已进行中心化（每列均值为0）：
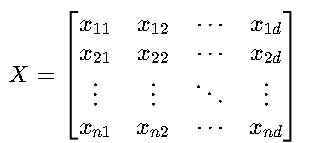
2. 计算协方差矩阵
协方差矩阵 Σ 反映特征间的线性关系，维度为 d×d：
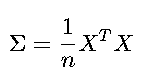
•计算示例：
若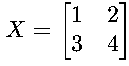
（已中心化后为 
）
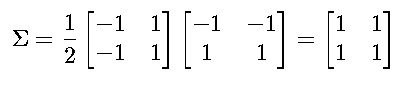3. 特征值分解
对 Σ 进行特征分解，得到特征值 λi 和特征向量 wi：
•W：特征向量矩阵（每一列为一个主成分方向）。
•Λ：对角矩阵，元素为特征值 λ1≥λ2≥⋯≥λd。
示例继续：
解 Σ 的特征方程 ∣Σ−λI∣=0：
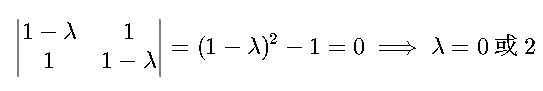
•对 λ1=2：特征向量 w1=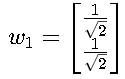
（单位化）。
对 λ2=0：特征向量 w2=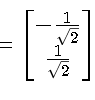
因此：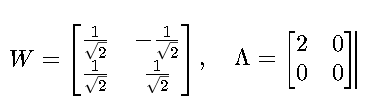
4. 选择主成分
按特征值从大到小排序，选择前 k 个特征向量（主成分）。
示例：若降维到 k=1，则选取 Wk=w1。
5. 数据投影
将原始数据投影到主成分空间，得到降维后的数据 Z：
示例：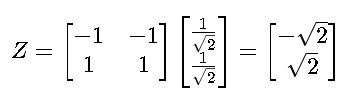
6. 方差解释率
计算各主成分的贡献率（解释方差比例）：
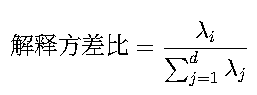
示例：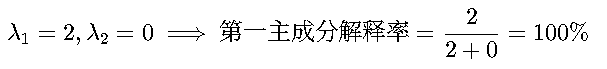
PCA的优缺点 •优点： • 显著降低计算复杂度：通过将高维特征空间投影到低维子空间，可减少后续计算所需的时间和存储资源。同时能有效去除噪声和冗余特征，提升模型性能。 • 最大化保留数据的主要方差信息：通过选择贡献率最高的主成分，通常能保留85%-95%的原始数据方差。这使得降维后的数据仍能反映原始数据结构，并可实现高维数据的可视化（如将数百维数据降至2D/3D以便观察数据分布）。 • 算法实现简单：成熟的数学理论基础和广泛的开源实现（如scikit-learn中的PCA模块）。
•缺点： • 基于线性变换假设：PCA只能捕捉线性相关性，对非线性数据结构（如流形、螺旋结构）效果不佳。此时可考虑核PCA（通过核函数处理非线性）或t-SNE等非线性降维方法。 • 降维后特征失去可解释性：主成分是原始特征的线性组合，不再对应具体的物理意义（如将"身高"和"体重"合并为一个新特征后，难以直接解释其含义）。 • 对数据尺度敏感：PCA基于方差最大化，不同量纲的特征需要先标准化处理。同时异常值会显著影响协方差矩阵的计算，需提前进行异常值检测和处理（如使用Z-score或IQR方法）
应用场景 •图像处理：
人脸识别（Eigenfaces）：通过PCA提取面部主要特征，将数万像素的人脸图像压缩为几十个关键特征维度图像压缩：在JPEG等格式中，利用PCA类似的原理（如DCT变换）减少存储空间
•生物信息学： - 基因表达数据分析：处理具有数万个基因但样本量有限的"高维小样本"数据，识别关键基因表达模式 - 蛋白质结构分析：从大量光谱数据中提取主要成分
•金融领域： - 风险因子分析：从数百个宏观经济指标中提取主要风险因子 - 投资组合优化：识别影响资产价格的关键驱动因素
•机器学习预处理： - 作为分类任务（如SVM、随机森林）的前置步骤，缓解维度灾难问题 - 在聚类分析（如K-means）前降维，提高算法效率和可视化效果 - 与其他特征选择方法（如Lasso）结合使用，构建更高效的模型
3.python应用
class sklearn.decomposition.PCA( n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None )
核心参数
参数 | 类型 | 说明 |
|---|---|---|
| int, float, 'mle' | 保留的主成分数量。若为 |
| {'auto', 'full', 'arpack', 'randomized'} | SVD求解器选择 |
| bool | 是否白化数据（单位方差） |
关键方法
方法 | 说明 |
|---|---|
| 拟合模型到数据 |
| 降维转换 |
| 拟合并转换 |
| 反向重构原始数据 |
属性
属性 | 说明 |
|---|---|
| 主成分轴（每行是一个主成分） |
| 各主成分的方差 |
| 各主成分方差占比 |
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
'''绘制混淆矩阵'''
def polt_matrix(x,y):#x:真实标签，y:测试标签from sklearn.metrics import confusion_matriximport matplotlib.pyplot as pltcm = confusion_matrix(x,y)plt.matshow(cm,cmap=plt.cm.Blues)plt.colorbar()for i in range(len(cm)):for j in range(len(cm)):plt.annotate(cm[i][j], xy=(j,i), horizontalalignment='center', verticalalignment='center')plt.ylabel('True label')plt.xlabel('Predicted label')return plt
'''画图'''
def plot_z(data):import matplotlib.pyplot as pltfrom pylab import mplmpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']mpl.rcParams['axes.unicode_minus'] = Falselables_count = pd.value_counts(data['Class'])print(lables_count)ax=lables_count.plot(kind='bar')ax.set_title('正负例样本数', fontsize=14)ax.set_xlabel('类别', fontsize=12)ax.set_ylabel('频数', fontsize=12)plt.show()
'''数据预处理'''
data = pd.read_csv('../逻辑回归/creditcard.csv')
'''
z标准化
'''
from sklearn.preprocessing import StandardScalerscaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])#二维数据，z标准化
data = data.drop('Time', axis=1)'''切分数据集'''
X_train = data.drop('Class', axis=1)
Y_train = data.iloc[:,-1]'''PCA降维'''
from sklearn.decomposition import PCA
pca = PCA(n_components=20)
X_train_pca = pca.fit_transform(X_train)
'''过采样，降维后'''
x_1train, x_1test, y_1train, y_1test = \train_test_split(X_train, Y_train, test_size=0.2, random_state=0)
from imblearn.over_sampling import SMOTEseed = SMOTE(random_state=0)
x_1train, y_1train = seed.fit_resample(x_1train, y_1train)
'''过采样，解决样本不均衡'''
x_train, x_test, y_train, y_test = \train_test_split(X_train_pca, Y_train, test_size=0.2, random_state=0)
#smote算法
from imblearn.over_sampling import SMOTEseed = SMOTE(random_state=0)x_train, y_train = seed.fit_resample(x_train, y_train)'''惩罚因子，交叉验证'''
#
from sklearn.model_selection import cross_val_scorescores = []
c_param_range = [0.01,0.1,1,10,100]#遍历c_param参数列表
for c_param in c_param_range:lr = LogisticRegression(C=c_param,penalty='l2',solver='lbfgs',max_iter=1000)score = cross_val_score(lr, x_train, y_train, cv=8,scoring='recall')scores_m = sum(score)/len(score)scores.append(scores_m)# print(scores_m)best_param = c_param_range[np.argmax(scores)]
print('最佳惩罚因子为：',best_param)lr = LogisticRegression(C=best_param,penalty='l2',max_iter=1000)
lr.fit(x_train, y_train)le = LogisticRegression(C=100,penalty='l2',max_iter=1000)
le.fit(x_1train, y_1train)
y_1pred = le.predict(x_1test)
# #混淆矩阵y_spred = lr.predict(x_train)
y_pred = lr.predict(x_test)
result = lr.score(x_test, y_test)
# polt_matrix(y_train, y_spred).show()
# polt_matrix(y_test, y_pred).show()print(result)
from sklearn import metrics
print('降维前:',metrics.classification_report(y_1test,y_1pred))# print('降维后自测：',metrics.classification_report(y_train, y_spred))
print('降维后测试：',metrics.classification_report(y_test, y_pred))#获得测试集测试报告