关于pygsp引发的一系列问题和实例小demo
关于pygsp引发的一系列问题和实例小demo
前言
忘记把错误复制下来了,反正要么是运行代码不出图然后pycharm进程崩溃退出,要么就是说numpy版本过高代码报错,要么就是报错说没有matplotlib.png。。。。给整红温了
解决方法
先把 numpy/scipy/matplotlib 固定到兼容的版本,再安装 pygsp,并且用 --no-deps 阻止它再次触发 scipy 和 numpy 的升级(一定要禁止它这令人无语的自动升级)
# 先激活名为radar的conda环境
(base) C:\Users\wu520>conda activate radar
# 先把易触发升级链的包卸掉
(radar) conda remove pygsp scipy numpy -y
# 安装依赖
(radar) pip install "numpy==1.26.4" -i https://pypi.tuna.tsinghua.edu.cn/simple
(radar) pip install "scipy==1.11.4" -i https://pypi.tuna.tsinghua.edu.cn/simple
:: 可选:把 matplotlib 升到更稳的 3.8 分支
(radar) pip install "matplotlib==3.8.4" -i https://pypi.tuna.tsinghua.edu.cn/simple
# 最后装 PyGSP,但禁止它自动装/升级依赖,避免再把 SciPy 升到 1.15.x、进而拉升到 NumPy 2.x
(radar) pip install "pygsp==0.5.1" --no-deps -i https://pypi.tuna.tsinghua.edu.cn/simple
测试代码
from pygsp import graphs, filters
G = graphs.Logo()
G.estimate_lmax()
g = filters.Heat(G, tau=100)import numpy as np
DELTAS = [20, 30, 1090]
s = np.zeros(G.N)
s[DELTAS] = 1
s = g.filter(s)
G.plot_signal(s, highlight=DELTAS, backend='matplotlib')
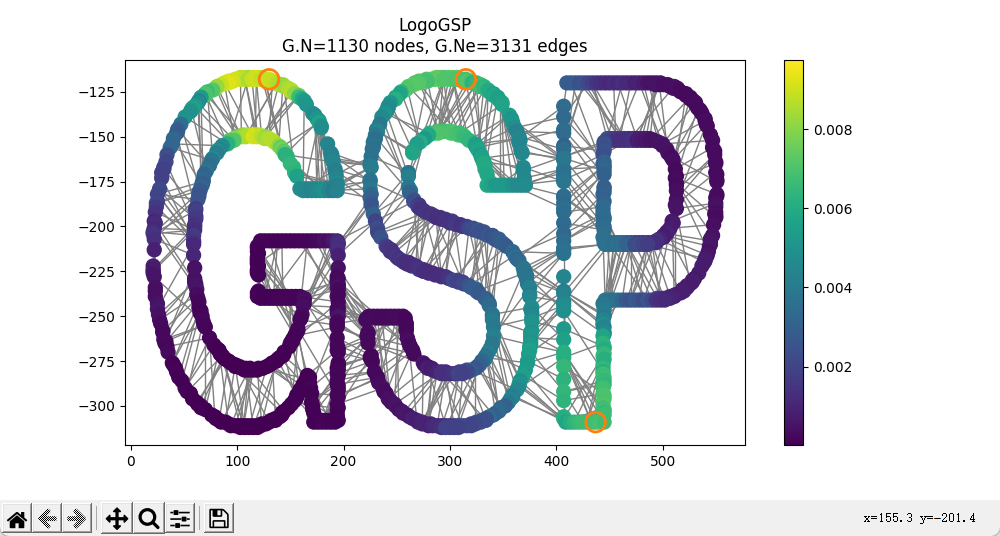
实例小demo——低通滤波
展示内容:
- 构造图与拉普拉斯,计算傅里叶基 U、特征值 λ
- 构造一条“分段常数 + 噪声”的图信号(在环的一半为 +1,另一半为 -1)
- 做 GFT 得到频谱,设计热核低通 g(λ) 并滤波 y = U g(Λ) U^T x
- 对比滤波前后:节点域信号、频谱、Dirichlet 能量 x^T L x(平滑度)
import numpy as np
import matplotlib.pyplot as plt
from pygsp import graphs, filters, plotting# ---- 让 PyGSP 用 matplotlib 作为绘图后端 ----
plotting.BACKEND = 'matplotlib'# ---- 中文显示(可选)----
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False# =========================
# 1) 构造图:N 节点的环图(无向、无权)
# =========================
N = 64
G = graphs.Ring(N=N) # 相当于 1D 周期网格
G.compute_fourier_basis() # 得到拉普拉斯特征分解:U, Λ(在 G.U, G.e)# 便捷引用
U = G.U # (N, N),列为特征向量(图傅里叶基)
lam = G.e # (N, ),对应特征值,升序;lam[0]≈0 为最低频
L = G.L.toarray() # 拉普拉斯矩阵(组合型)# =========================
# 2) 构造一条图信号:分段常数 + 噪声
# 直觉:边界处变化大 → 高频分量多
# =========================
x = np.ones(N, dtype=float)
x[N//2:] = -1.0
rng = np.random.default_rng(42)
x_noisy = x + 0.25 * rng.standard_normal(N)# 图傅里叶变换(GFT)与逆变换(IGFT)
def gft(sig): # \hat{x} = U^T xreturn U.T @ sigdef igft(spec): # x = U \hat{x}return U @ specX_hat = gft(x_noisy)# =========================
# 3) 设计一个低通滤波器并滤波
# 常用两类:热核 exp(-tau λ);Tikhonov 1/(1+tau λ)
# =========================
tau = 2.0
g = filters.Heat(G, tau=tau) # 直接用 PyGSP 的热核(等价于 g(λ)=exp(-τλ) 的低通)
# 也可自定义:g = filters.Filter(G, lambda l: 1/(1+tau*l))y = g.filter(x_noisy) # 频域缩放 + 逆变换 已内置实现
Y_hat = gft(y) # 为了画图对比,把滤后也做一次 GFT# =========================
# 4) 计算 Dirichlet 能量(平滑度): x^T L x
# 值越小越“平滑”,邻居差值越小
# =========================
def dirichlet_energy(sig):return float(sig.T @ L @ sig)E_x = dirichlet_energy(x_noisy)
E_y = dirichlet_energy(y)
print(f"Dirichlet 能量(平滑度指标): 原始 {E_x:.3f} → 低通后 {E_y:.3f}")# =========================
# 5) 可视化
# =========================# (a) 在环上画节点取值(PyGSP 自带绘制)
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
G.set_coordinates('ring2D') # 让坐标呈环形
G.plot_signal(x_noisy, ax=axes[0])
axes[0].set_title("原始图信号(带噪)")
axes[0].set_axis_off()G.plot_signal(y, ax=axes[1])
axes[1].set_title(f"低通滤波后(热核 τ={tau})")
axes[1].set_axis_off()
fig.tight_layout()# (b) 频谱对比:|X̂(λ)| vs |Ŷ(λ)|
fig, ax = plt.subplots(figsize=(9, 3))
ax.stem(lam, np.abs(X_hat), basefmt=" ", label=r'$|\hat{X}(\lambda)|$ 原始', use_line_collection=True)
ax.stem(lam, np.abs(Y_hat), basefmt=" ", linefmt='C1-', markerfmt='C1o',label=r'$|\hat{Y}(\lambda)|$ 低通后', use_line_collection=True)
ax.set_xlabel("特征值 λ(频率指标,越大越高频)")
ax.set_ylabel("谱系数幅值")
ax.set_title("图频谱对比")
ax.grid(alpha=0.3)
ax.legend()
plt.tight_layout()# (c) 沿节点索引画折线,更直观看“平滑化”效果
fig, ax = plt.subplots(figsize=(9, 3))
ax.plot(x_noisy, '-o', ms=3, label='原始(带噪)')
ax.plot(y, '-o', ms=3, label='低通后')
ax.set_title("沿环的节点序列(相邻差值小=更平滑)")
ax.set_xlabel("节点索引")
ax.set_ylabel("节点取值")
ax.grid(alpha=0.3)
ax.legend()
plt.tight_layout()# (d) 画出滤波器频响(理论 g(λ)=exp(-τλ))
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(lam, np.exp(-tau * lam), '-o', ms=3)
ax.set_xlabel("λ")
ax.set_ylabel("g(λ)")
ax.set_title("低通频率响应(热核)")
ax.grid(alpha=0.3)
plt.tight_layout()plt.show()
结果展示
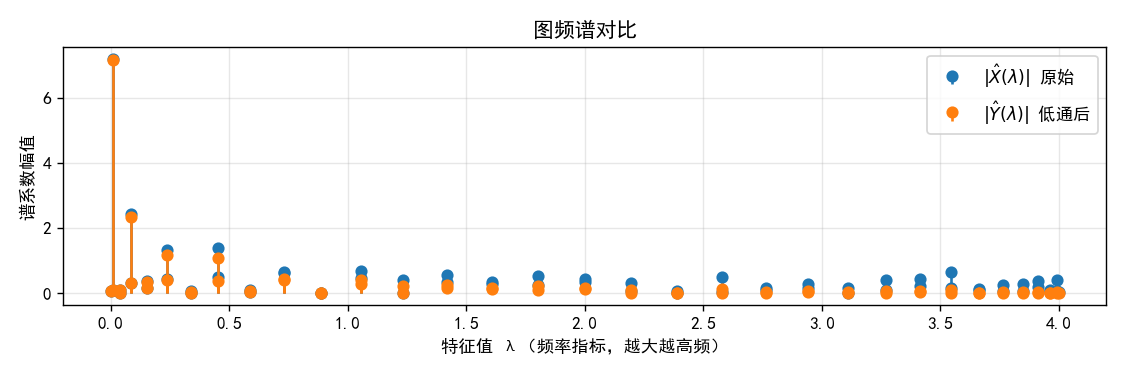
- 横轴是拉普拉斯特征值 λ\lambdaλ(越大代表越高的图频率)。
- 蓝色是滤波前的谱幅度 ∣X^(λ)∣|\hat{X}(\lambda)|∣X^(λ)∣,橙色是滤波后的 ∣Y^(λ)∣|\hat{Y}(\lambda)|∣Y^(λ)∣。
- 现象:低通把大 λ\lambdaλ 区域(高频)显著压低,而小 λ\lambdaλ 区域(低频)保留较多。
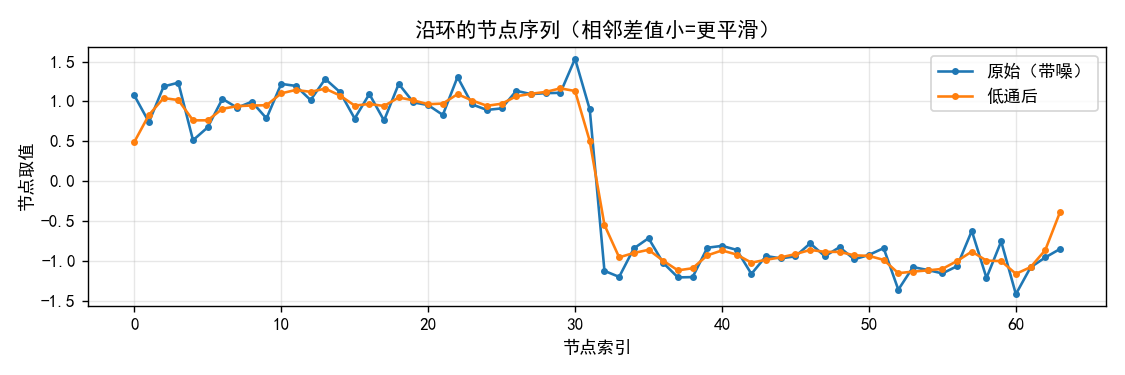
- 蓝线是带噪的分段常数信号(前半区 ≈+1\approx +1≈+1,后半区 ≈−1\approx -1≈−1)。
- 橙线是热核低通 g(λ)=e−τλg(\lambda) = e^{-\tau\lambda}g(λ)=e−τλ,τ=2\tau = 2τ=2 之后的结果。
- 现象:噪声被抑制,相邻节点更平滑,但在“边界”(从 +1+1+1 到 −1-1−1 的跃迁处)仍保留结构。
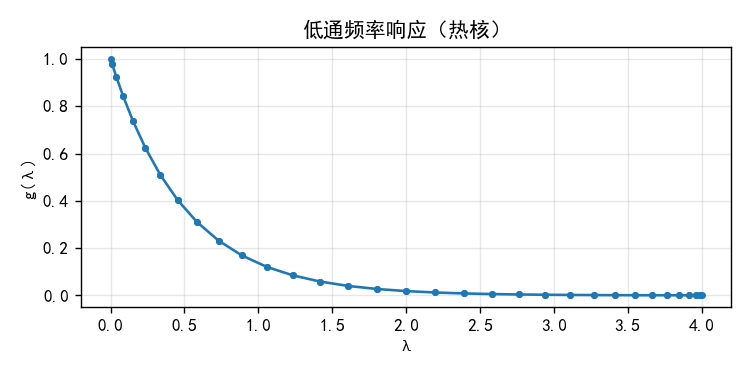
- 展示 g(λ)=exp(−τλ)g(\lambda) = \exp(-\tau\lambda)g(λ)=exp(−τλ) 的频率响应,λ\lambdaλ 越大,响应越小(强低通)。
Dirichlet 能量(平滑度指标): 原始 13.147 → 低通后 3.261
- 计算了图信号的平滑度指标 x⊤Lxx^\top L xx⊤Lx。
- 显示滤波显著降低了相邻节点差异,信号在图上更“平滑”。
