当前位置：首页 > ds >正文

CS231n-2017 Lecture5卷积神经网络笔记

ds 2025/7/23 15:17:35

卷积神经网络(CNN):

卷积神经网络与常规神经网络相似，都由神经元层连接而成，区别在于CNN基于输入数据为图像的假设，从而使结构发生了相应地变化

结构：

卷积神经网络各层中的神经元为三维排列的，包含宽度、高度和深度，且层中的神经元只与前一层的部分区域连接，而不是全连接，最后输出是把全尺寸图像压缩为包含评分的一个向量，在深度方向排列

卷积网络的各种层：

主要由三种类型的层构成：卷积层，汇聚层(Pooling)和全连接层

卷积层：

滤波器(filter)/卷积核(kernel)：

一个小size的三维数组，其长和宽自定，深度一般与输入相同，例如，现在有 $[5\times5\times3]$ 的一个滤波器，输入图像为 $[32\times32\times3]$ ，则这个滤波器会在输入的长与宽上滑动，每滑动一步，就与对应的输入区域做点积（对应位置元素相乘，再求和），得到一个标量，假设这里每一步滑动一个像素，那么每一步得到的标量排列起来，最终得到的输出就是一个 $[28\times28\times1]$ 的张量

filter的size称为感受野(receptive field)

卷积层由n个size相同的滤波器组成，则将n个滤波器输出的张量叠在一起，就会得到一个深度为n的张量输出

局部连接：

之前讨论的神经网络是全连接的，也就是说一个神经元对应输入的每一个元素都有独立的权重，但是在卷积层中，一个神经元不一定能够接触到输入的所有元素，因此只是局部连接。除此之外，我们研究一个滤波器，会发现一个神经元的权重同样应用于所有它能够接触到的输入的元素，因此神经元权重的数量大大减少，也称之为参数共享。例如上文的 $[5\times5\times3]$ 的filter，则其总共只需要 $5\times5\times3=75$ 个权重（准确地说，还需要加上1个偏置）。注意这个时候在反向传播的时候，需要计算每个神经元对其权重的梯度，再将统一深度的所有神经元对权重的梯度累加，进而得到共享权重的梯度

参数共享并不是在任何情况都适用，因为它建立在这样的一个假设基础上：如果图像在某些地方探测到的一个水平边界是十分重要的，那么在其他的一些地方也是同样有用的，因为图像结构具有平移不变性。但如果输入图像是一些明确的中心结构的图像，例如人脸时，我们希望不同的特征（比如眼睛、头发特征）会在图片的不同位置被学习，这个时候，我们就放宽松参数共享的限制，也就是说，不是所有位置的kernel都实现参数共享，称之为所谓的局部连接层。

控制输出size的超参数：

深度(depth)：

输出的depth由filter的个数决定，数值上就等于filter的个数

步长(stride):

filter每次移动的像素长度，显然会影响输出的长和宽

0填充(padding)：

对输入数据在边缘处使用0填充扩展（每填充一次就是四周都填充），进而控制其size，最常见的是使其长宽相等

计算输出size的公式：

假设输入size为W，感受野size为F，步长为S，零填充数量为P，则输出的size为(W-F+2P)/S+1

如图例：

这里只有1维x轴，最右边是感受野及其权重，偏置为0

对于左1来说，其W=5,P=1,S=1，则输出size为(5-3+2)/1+1=5

对左2来说，其S=2，则输出size为(5-3+2)/2+1=3

步长的限制：

注意这些空间排列的超参数之间是相互限制的，我们必须要合理地调整，使得输出的size为整数，若不是整数，说明感受野不能够整齐对称地滑过输入数据，则此时超参数的设定无效

卷积效果演示如下图：

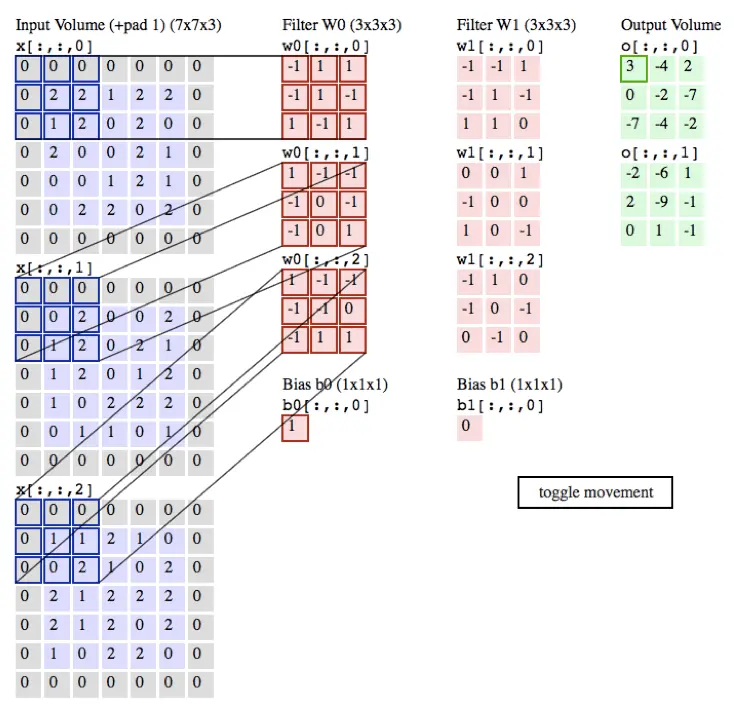
使用矩阵乘法实现卷积：

卷积运算本质是kernel与输入数据的局部区域间作点积，卷积层的常用实现方法就是利用这一点，将卷积层的前向传播变成一个巨大的矩阵乘法

1.将输入图像的局部区域展开成列向量，例如，输入为 $[227\times227\times3]$ ,kernel为 $[11\times11\times3]$ ，stride = 4，则我们取每一步所对应输入的局部区域，将其展开成 $11\times11\times3 = 363$ 个元素的列向量，重复进行该过程，由于输出的size为 $(227-11)/4+1 = 55$ ，则输出应为 $55\times55 = 3025$ 个元素，即我们将每一步展开的列向量按列排列，得到 $[363\times3025]$ 的矩阵X

2.将卷积层的权重展开成行向量，如，若有96个kernel，按行排列96个行向量得到 $[96\times363]$ 的矩阵W

3.这样一来，卷积的结果就等价于 $WX$ ，得到一个 $96\times3025$ 的输出

4.最后我们重新整理该矩阵的size，首先96被整理成深度，3025要按照之前将 $55\times55=3025$ 的逆向步骤压缩回 $55\times55$ ，进而将输出size变回 $[55\times55\times96]$

这个方法的缺点是展开矩阵的时候占用内存太多，因为输入矩阵的元素在X中被多次复制，但优点是矩阵乘法可以被高效算法加速运算

汇聚层(Pooling)：

通常，会在连续的卷积层中周期性地插入一个汇聚层，其作用是逐渐降低数据的size，从而减少网络中参数的个数，使得计算资源消耗减少，并有效控制过拟合

最大汇聚(MAX Pooling):

MAX Pooling采用MAX操作，对输入数据的每一个深度切片独立进行操作，最常见的形式如下：

使用size为 $2\times2$ 的filter，以stride = 2来对每个深度切片进行降采样，从框选出的4个元素中选取最大值，丢弃掉剩下的75%的信息，从而在保持一定输入信息的前提下减小size

Pooling很少使用0填充

公式如下：

输入size: $W_1 \times H_1 \times D_1$

超参数：

filter的size: $F$

步长 $S$

输出size: $W_2 \times H_2 \times D_2$

则 $W_2 = (W_1 - F)/S+1$

$H_2 = (H_1 - F)/S + 1$

$D_2 = D_1$

MAX Pooling参数通常只有两种形式：

1. $F=3, S=2$ ，称重叠汇聚(overlapping)

2. $F=2,S=2$

对更大的receptive field进行Pooling所需的Pooling size更大，而且对网络更具有破坏性

反向传播：

MAX Pooling使用max函数，可以简单理解为梯度指沿着最大的输入回传，因此，在前向传播经过MAX Pooling时，通常会把最大元素的index记录下来（称之为道岔(switches)），这个时候在反向传播的时候计算较为高效

普通汇聚(General Pooling):

顾名思义，MAX操作变成了取平均值操作，但效果不如MAX Pooling，现在已经很少使用

归一化层：

有很多不同类型的归一化层，但实践证明它们的效果十分有限，因此这里不作讨论

全连接层与卷积层的相互转化：

全连接层与卷积层之间唯一的不同就是卷积层中的神经元只与输入数据中的一个局部区域连接，并在卷积列中的神经元共享参数

卷积层转换为全连接层：

对于转换出来的全连接层的权重矩阵，有部分会是0（由于局部连接），大部分块中，很多元素重复相等（参数共享）

全连接层转换为卷积层：

对于一个全连接层，假设其输出向量维度是K，我们可以把其看作是拥有K个size和输入数据size一致的kernel得到的 $[1\times1\times K]$ 的张量，再将其resize为向量即可

这样做有什么用呢？可以高效地实现滑动kernel卷积

例如：

我们已经训练好了一个用于图像分类的CNN，其输入size是固定的，为 $[224\times224]$ ，现在，我想要用这个网络在一张更大的图片，比如 $[384\times384]$ 上检测多个区域（例如不同位置的物体）

最直接的办法（低效）：在大图中裁剪出一个 $[224\times224]$ 的窗口 -> 送入网络计算得分 ->将窗口滑动到向下一个位置（比如步长32像素） -> 重复过程直到覆盖整张大图。这样的问题在于，如果大图上需要检测的位置很多，比如 $6\times6 = 36$ 个位置，我们就需要进行36次独立的前向传播，就会非常地耗时

全连接层转卷积层：

假设在原CNN经过conv和pooling后连接到最后一个全连接层的输入是 $[7\times7\times512]$ ，输出维度是1000，这个FC层可以看作是一个巨大的矩阵乘法

我们将其权重矩阵W重塑成1000个 $[7\times7]$ 的kernel，步长为1，0填充为0，这和我们上述的全连接层转卷积层的方法一致

如果我们把网络中的全部全连接层都转换成等效的卷积层，那么我们的网络就变成了全卷积网络(Fully Convolutional Network, FCN)，这种FCN可以直接接收任意尺寸的图片作为输入，并输出一个size与输入成正比的特征图，而不再是固定长度的向量

回到上面的例子

假设我们的CNN是经过卷积层增加通道数和5次Pooling，使244缩小至7的，最后经过一个卷积层（全连接层转换而来）

那么对于更大的size $[384\times 384]$ ，其先经过卷积层和5次Pooling得到 $[12\times12\times512]$ 的特征图，将这个特征图作用到最后一个卷积层上，则其输出 $size = (12 - 7)/ 1 + 1 = 6$ ，所以输出为 $[6\times6\times1000]$ ，这36个1000维度的向量，恰好对应了之前划分出来的大图36个不同位置的得分向量

由此可见，这样，我们只需要1次前向传播，就可以得到全部36个位置的分类得分，比之前使用全连接层的36次前向传播要高效很多，因为这里卷积层的滑动的36次计算都是在共享资源进行计算

更小的步长分割子图：

最后，由于上面 $[384\times384]$ 缩小到的size是 $[12\times12]$ ，说明缩小后的1个像素点对应着原图 $[32\times32]$ 的像素点，所以我们在使用全连接层转化而来的卷积层的时候，只能得到步长为32分割出来的 $6\times6$ 个子图。如果我们想要使步长比32更小，例如16来分割子图，又想继续使用全连接层转化的卷积层，要怎么办呢？