C++数据结构之二叉搜索树

一.二叉搜索树概念及相关特性

1.二叉搜索树的概念

⼆叉搜索树⼜称⼆叉排序树，它或者是⼀棵空树，或者是具有以下性质的⼆叉树:

• 若它的左⼦树不为空，则左⼦树上所有结点的值都⼩于等于根结点的值

• 若它的右⼦树不为空，则右⼦树上所有结点的值都⼤于等于根结点的值

• 它的左右⼦树也分别为⼆叉搜索树

•二叉搜索树的中序遍历会得到一个有序的序列

• ⼆叉搜索树中可以⽀持插⼊相等的值，也可以不⽀持插⼊相等的值，具体看使⽤场景定义，后续我们学习map/set/multimap/multiset系列容器底层就是⼆叉搜索树，其中map/set不⽀持插⼊相等

值，multimap/multiset⽀持插⼊相等值

2.二叉搜索树的性能

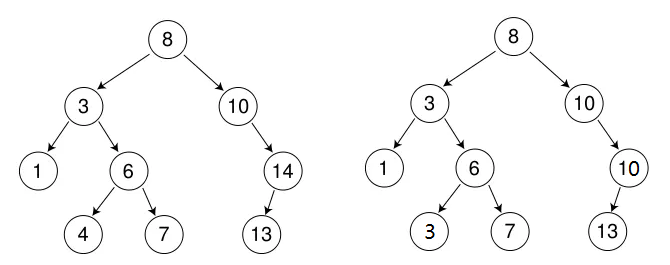
最优情况下，⼆叉搜索树为完全⼆叉树(或者接近完全⼆叉树)，其⾼度为： log2 N 最差情况下，⼆叉搜索树退化为单⽀树(或者类似单⽀)，其⾼度为： N

所以综合⽽⾔⼆叉搜索树增删查改时间复杂度为： O(N)

那么这样的效率显然是⽆法满⾜我们需求的，我们后续需要继续讲解⼆叉搜索树的变形，平衡⼆叉搜索树AVL树和红⿊树，才能适⽤于我们在内存中存储和搜索数据。

这里的二叉搜索树是一种入门级别的搜索树，后面我们会深入讲解红黑树和AVL树等改良版本的搜索树，他们的查找性能更强。

3.二叉搜索树的插入

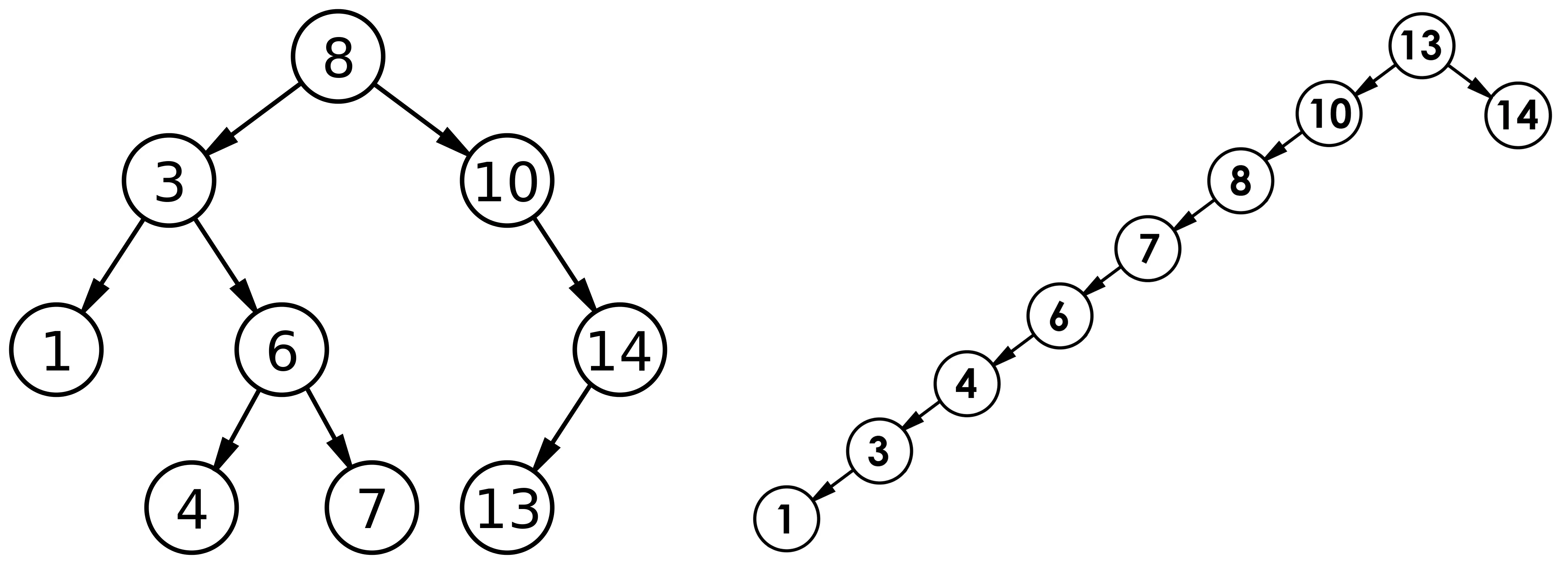
在插入结点时，若当前为空树：创建新结点，将root赋值给当前插入的结点。若不为空树，与当前结点值进行比较，大于则往右树走，小于则往左树走，直到找到合适的位置插入。注意，若插入的值有相等的，需要保持一致性，要往左都往左，要往右都往右。

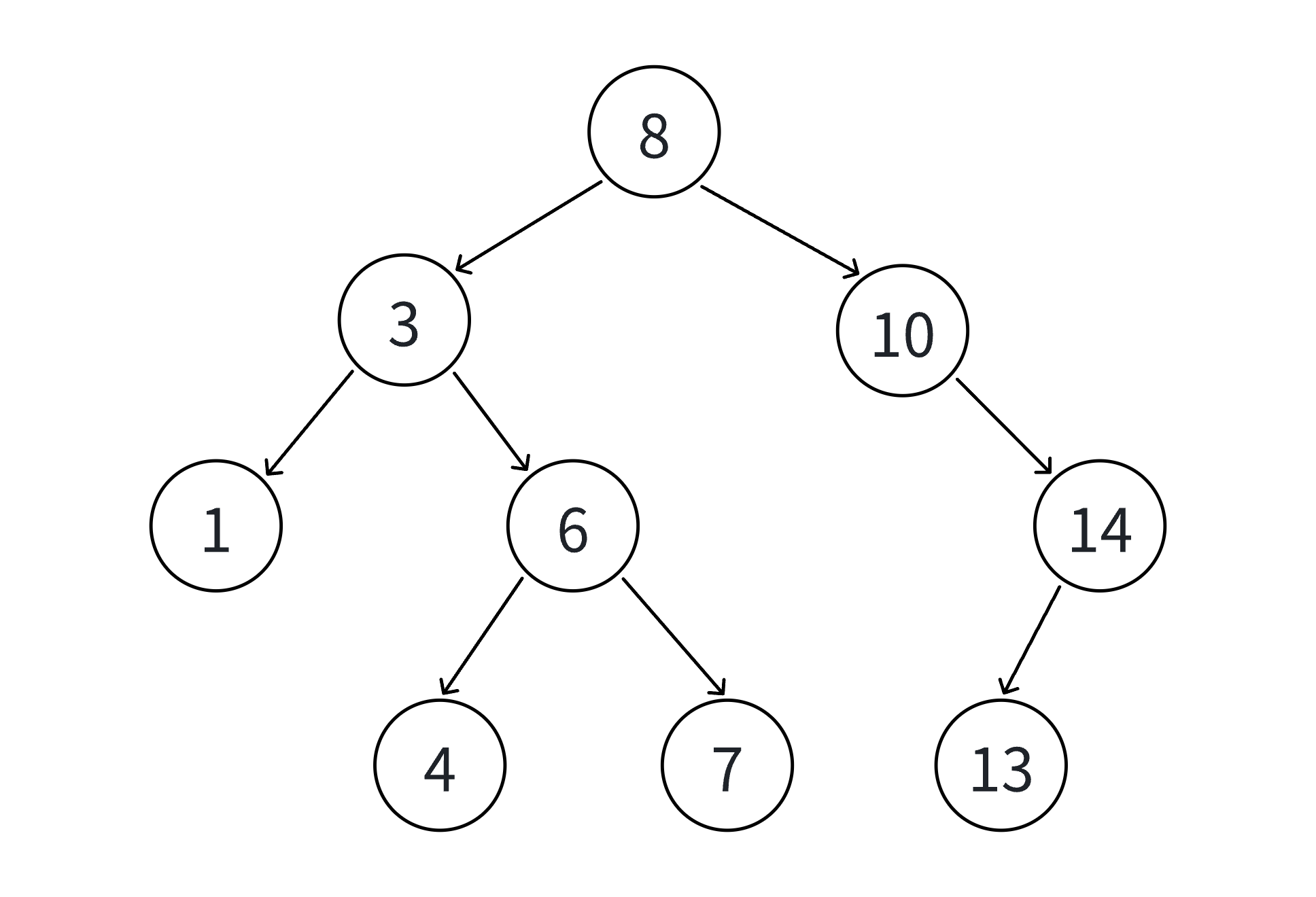
 int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};

4.二叉搜索树的查找

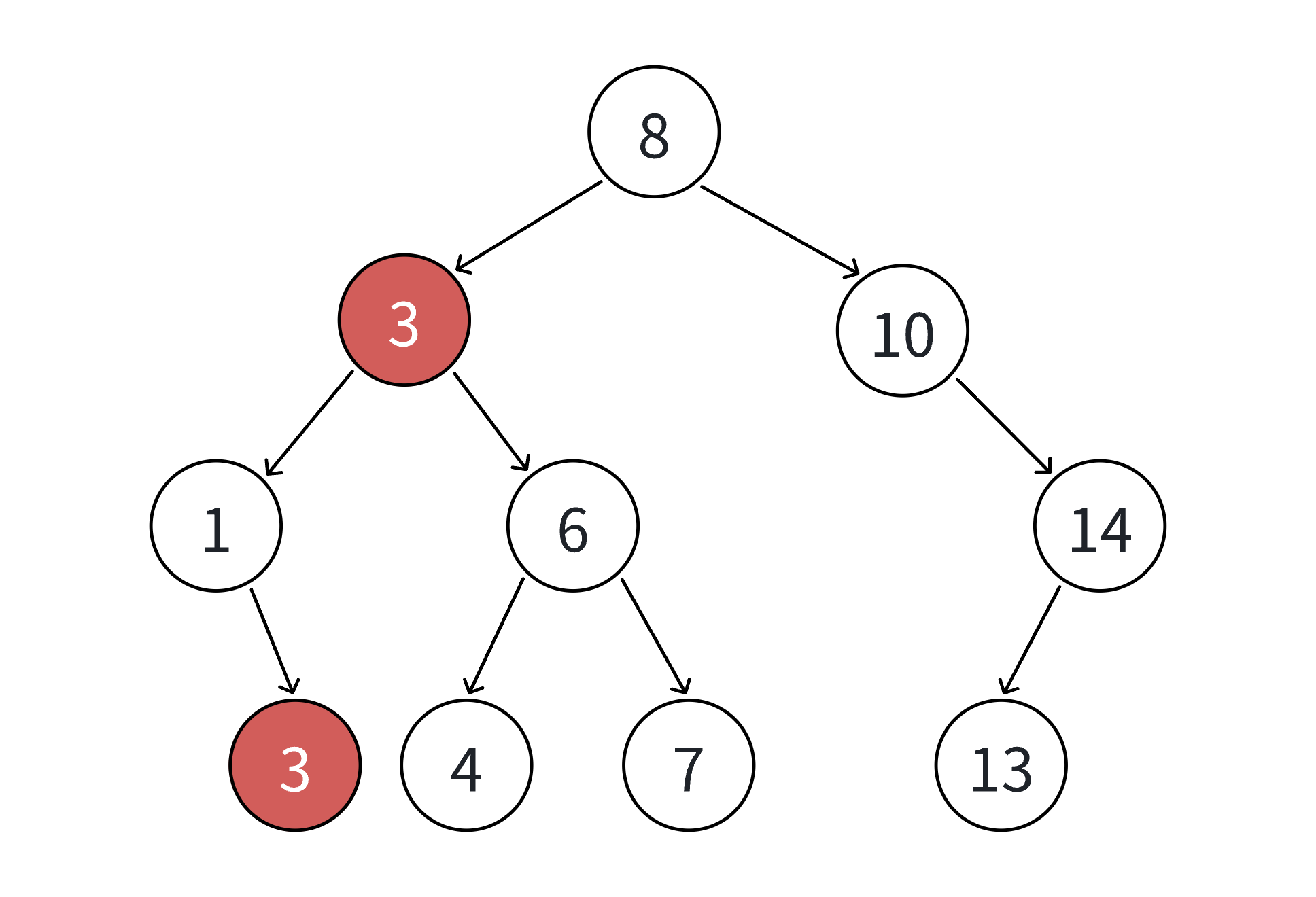
查找和插入的过程类似，查找值为X的结点，大于则往右树走，小于则往左树走。若树中由多个符合X的值的结点，则返回中序遍历的第一个值为X的结点。由二叉树的性能可知，最多查找高度次就停止查找。

5.二叉搜索树的删除

⾸先查找元素是否在⼆叉搜索树中，如果不存在，则返回false。

如果查找元素存在则分以下四种情况分别处理：（假设要删除的结点为N）

1. 要删除结点N左右孩⼦均为空

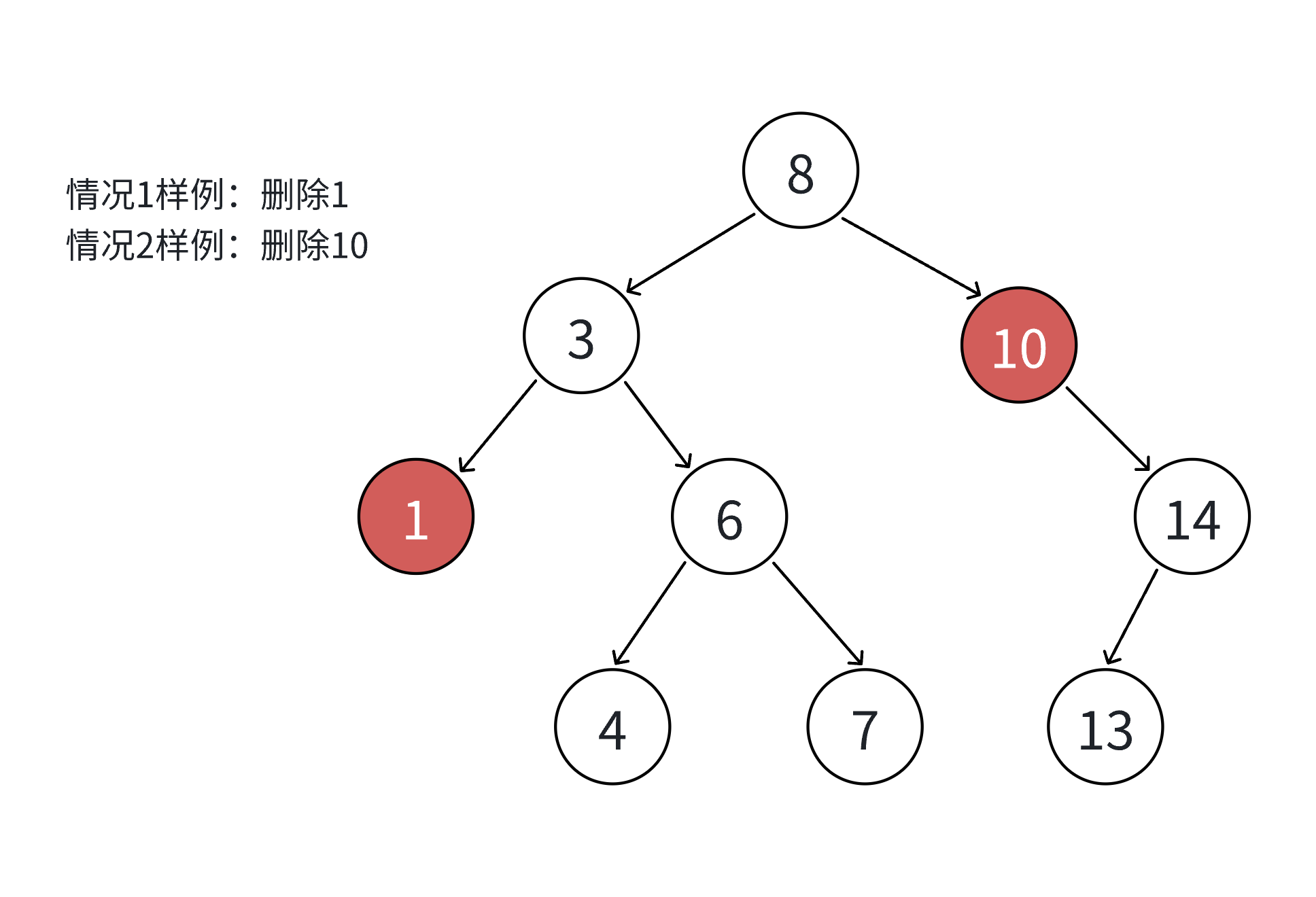
2. 要删除的结点N左孩⼦位空，右孩⼦结点不为空

3. 要删除的结点N右孩⼦位空，左孩⼦结点不为空

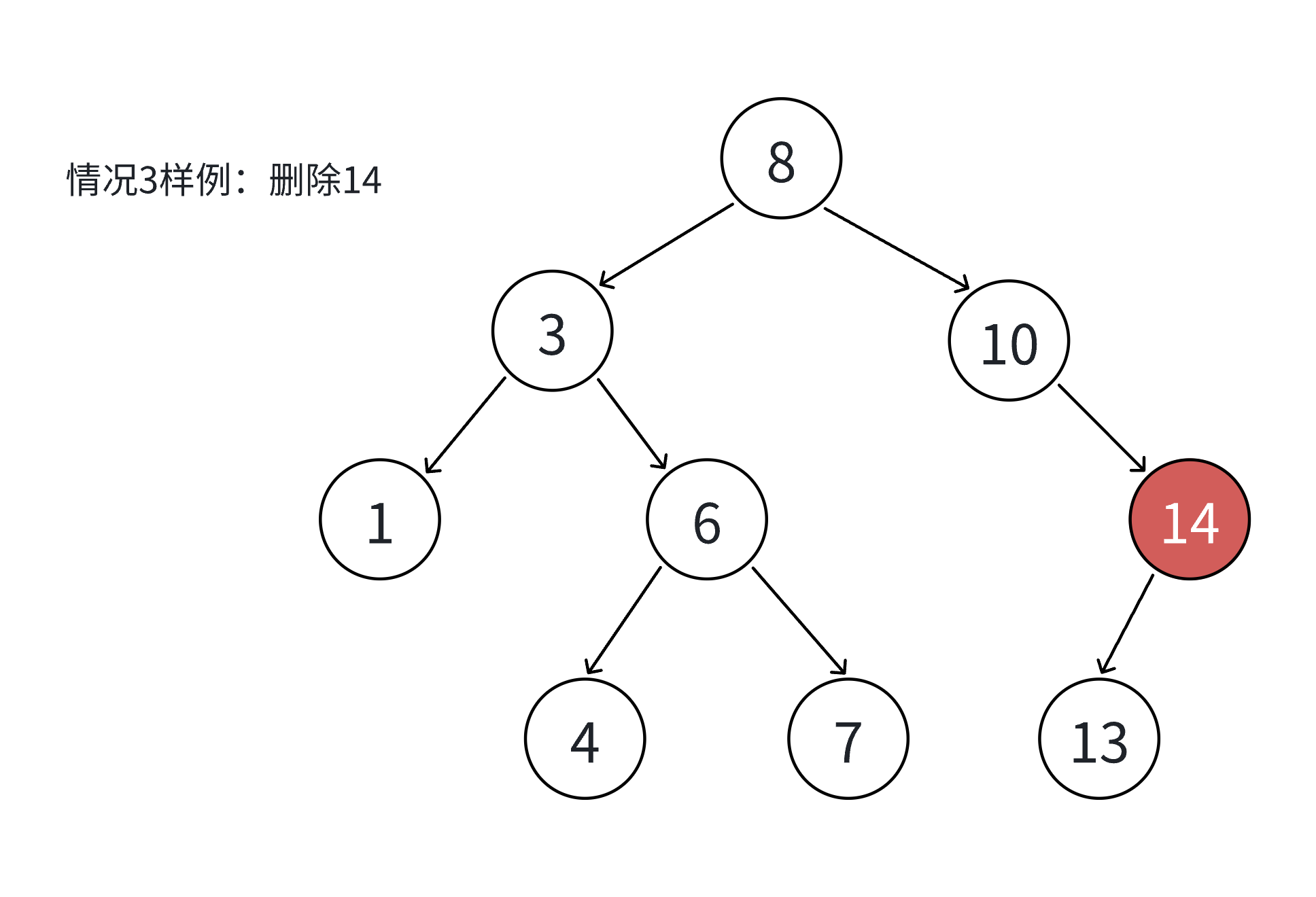
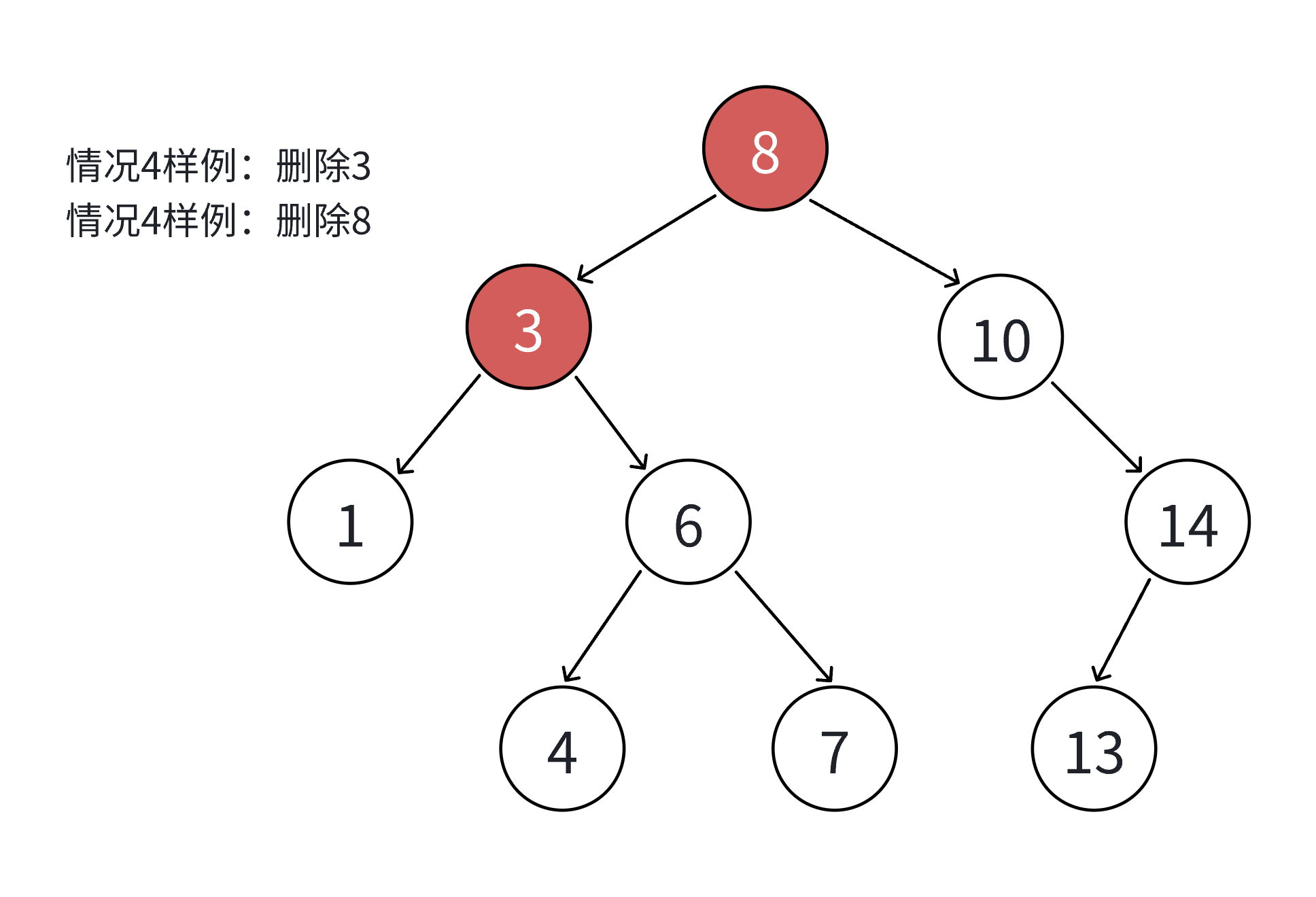
4. 要删除的结点N左右孩⼦结点均不为空

对应以上四种情况的解决⽅案：

1. 把N结点的⽗亲对应孩⼦指针指向空，直接删除N结点（情况1可以当成2或者3处理，效果是⼀样的）

2. 把N结点的⽗亲对应孩⼦指针指向N的右孩⼦，直接删除N结点

3. 把N结点的⽗亲对应孩⼦指针指向N的左孩⼦，直接删除N结点

4. ⽆法直接删除N结点，因为N的两个孩⼦⽆处安放，只能⽤替换法删除。找N左⼦树的值最⼤结点R(最右结点)或者N右⼦树的值最⼩结点R(最左结点)替代N，因为这两个结点中任意⼀个，放到N的位置，都满⾜⼆叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换，转⽽变成删除R结点，R结点符合情况2或情况3，可以直接删除。

二.key与key/value的二叉搜索树

1.key的搜索场景

如果学过一点python字典的知识，我们可以得知“键值对”这个概念，这也是下面我们要讲解的概念。而这里的key则是键，在生活中用key搜索的场景，往往key本身就是要搜索的信息，并且无法实现修改的操作。例如小区的停车场系统，系统只会录入业主的车辆信息，根据车牌号查找车辆是否在系统中，若不在则不会让车通过。

2.key的二叉搜索树实现

#pragma once
#include<iostream>
using namespace std;namespace key {template<class K>struct BSTNode {K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode(const K& key): _key(key), _left(nullptr), _right(nullptr) {}};template<class K>class BSTree {using Node = BSTNode<K>;public:bool Insert(const K& key) { if (_root == nullptr) {_root = new Node(key);return true;}Node*parent = nullptr;Node*cur = _root;while (cur) { if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {return false;}cur = new Node(key);if (key > parent->_key) {parent->_right = cur;}else {parent->_left = cur;}return true;}}bool Find(const K& key) {Node*cur = _root;while (cur) {if (key > cur->_key) {cur = cur->_right;}else if (key < cur->_key) {cur = cur->_left;}else {return true;}}return false;}bool Erase(const K& key) {Node*parent = nullptr;Node*cur = _root;//先去查找结点在哪while (cur) { if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}//找到了，根据不同的情况处理else {//左为空if (cur->_left == nullptr) {//此时若要删除的是左为空的根节点if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}//右为空else if (cur->_right == nullptr) {if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}//左右都不为空else { //用左树最大或者右树最小代替Node* replaceParent = cur;Node* replace = cur->_right;while (replace->_left){replaceParent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replaceParent->_left == replace)replaceParent->_left = replace->_right;elsereplaceParent->_right = replace->_right;delete replace;}return true;}}}//共有的方法将root作为参数传入并且递归，在公共类中直接取root是不合理的void InOrder() {_InOrder(_root);cout << endl;}
private:void _InOrder(Node* root) {if (root==nullptr) {return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;};
}

3.key/value的搜索场景

这个场景相对来说就比较好理解了，键值对的组合有很多例子，比如英汉互译词典：可以根据不同的英文单词找到其对应的解释。

4.key/value的搜索二叉树实现

#pragma once
#include<iostream>
using namespace std;namespace key_value
{template<class K, class V>struct BSTNode{K _key;V _value;BSTNode<K, V>* _left;BSTNode<K, V>* _right;BSTNode(const K& key, const V& value):_key(key), _value(value), _left(nullptr), _right(nullptr){}};// Binary Search Tree// Key/valuetemplate<class K, class V>class BSTree{//typedef BSTNode<K> Node;using Node = BSTNode<K, V>;public:// 强制生成构造BSTree() = default;BSTree(const BSTree& t){_root = Copy(t._root);}BSTree& operator=(BSTree tmp){swap(_root, tmp._root);return *this;}~BSTree(){Destroy(_root);_root = nullptr;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{// 右为空if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 左右都不为空// 右子树最左节点Node* replaceParent = cur;Node* replace = cur->_right;while (replace->_left){replaceParent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replaceParent->_left == replace)replaceParent->_left = replace->_right;elsereplaceParent->_right = replace->_right;delete replace;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key, root->_value);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}private:Node* _root = nullptr;};
}

5.关于搜索二叉树实现的细节

1.Insert时parent结点和cur结点的重要性

由于搜索二叉树独特的左小右大的性质，在插入一个结点时我们需要找到合适的位置，这就需要我们不断遍历整个二叉树。cur结点初始指向_root的位置，parent结点初始指向nullptr。遍历树时，要插入的结点值大于当前结点值，cur就往右子树走，相反的就往左子树走。而parent则是始终为cur的父结点，并随着查找不断更新。当cur找到一个合适的位置时不能直接插入，要将cur位置new一个树结点，接着需要将cur的结点与整棵树相连，因此parent结点也必不可少，我们需要时刻记录cur结点的父结点信息。

bool Insert(const K& key) { if (_root == nullptr) {_root = new Node(key);return true;}Node*parent = nullptr;Node*cur = _root;while (cur) { if (key > cur->_key) {parent = cur;cur = cur->_right;}else if (key < cur->_key) {parent = cur;cur = cur->_left;}else {return false;}cur = new Node(key);if (key > parent->_key) {parent->_right = cur;}else {parent->_left = cur;}return true;}}

2.中序遍历实现的细节

观察上面的代码不难发现，原本我们的中序遍历是写在私有部分的，并且在公共部分还右这样的代码

private:void _InOrder(Node* root) {if (root==nullptr) {return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}

void InOrder() {_InOrder(_root);cout << endl;}

这样做的原因如下：首先树的根结点作为私有成员，外部函数调用前序遍历时直接传入根结点肯定是不合理的

key::BSTree<int> t;
int a[] = { 8, 3, 1, 10, 1, 6, 4, 7, 14, 13};
for (auto e : a)
{t.Insert(e);
}
t._InOrder(_root);

但是直接将前序遍历写在私有成员中，也不太合理，我们外部无法直接调用此函数。有没有什么较好的解决方法呢？就是上面的在公共部分再写一个函数，因为一个类的内部是可以随便访问私有成员的，这样做既可以做到在外部直接调用前序遍历，还可以做到不暴露私有成员。（这里还有一个解决办法就是写一个getRoot方法取到根节点）

3.实现删除时左右孩子不为空的细节

删除左右孩子不为空的结点可以说是这里最复杂的一种情况，因为我们需要额外的处理方式：找到左子树的最大结点或者右子树的最小结点，将待删除结点的值改为这替代结点的值。实现起来也并不复杂，但是我们需要额外考虑一种情况：删除的恰好是根节点的情况

else { //用左树最大或者右树最小代替Node* replaceParent = nullptr;Node* replace = cur->_right;while (replace->_left){replaceParent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replaceParent->_left == replace)replaceParent->_left = replace->_right;elsereplaceParent->_right = replace->_right;delete replace;}

若此时将replaceParent的初始值设为nullptr，加入此时的替换结点恰好为根节点的右孩子。。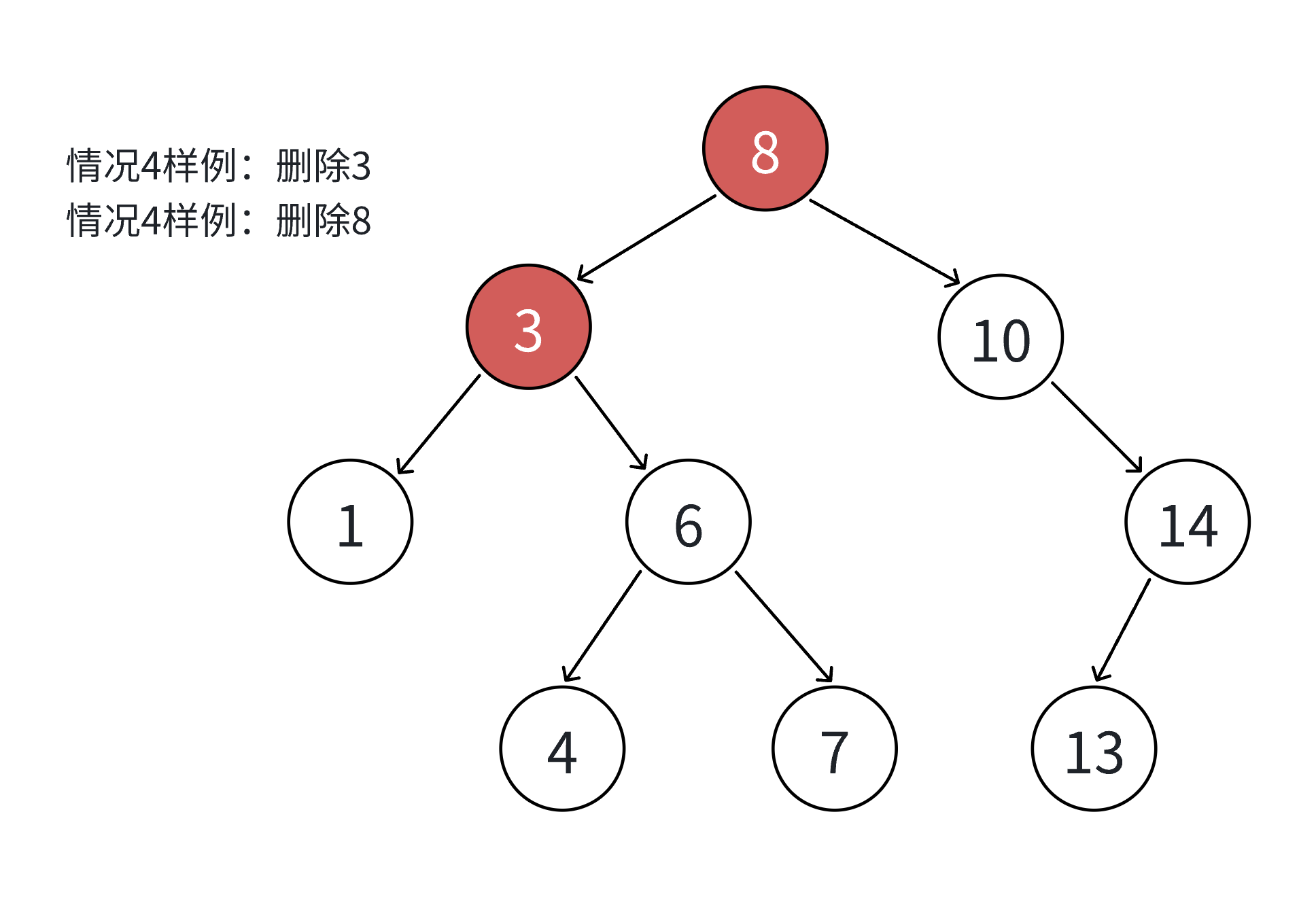

会发现根本没有进while循环。。。

这就导致了replaceParent的值依然为初始的nullptr，没进循环就无法更新它的值，所以这里删除8这个结点会报空指针错误。

4.搜索二叉树的拷贝和析构问题

二叉树的拷贝实际上是深拷贝。这是我们实现构造和析构的核心逻辑可以看到比较重要的一点就是析构的顺序是后序，而拷贝构造的顺序是前序

void Destroy(Node* root)
{if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;
}Node* Copy(Node* root)
{if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key, root->_value);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;
}

值得一提的是这里的赋值运算符重载，和之前我们实现链表的方式比较类似，巧妙运用传值传参产生的临时对象并且进行资源的swap操作

BSTree() = default;BSTree(const BSTree& t)
{_root = Copy(t._root);
}BSTree& operator=(BSTree tmp)
{swap(_root, tmp._root);return *this;
}~BSTree()
{Destroy(_root);_root = nullptr;
}

5.这里埋下一个坑

在测试key_value的功能时，写了这样一个例子：将一个数组中的字符串插入搜索二叉树，并统计各个单词出现的频率。值得注意的是这里Find函数的行为：若当前单词不存在，插入当前单词并将个数改为1。若存在则直接令当前的单词的value++。这个动作会和后面讲到的map和set的Find有关。

string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉" };
key_value::BSTree<string, int> countTree;for (const auto& str : arr)
{// 先查找水果在不在搜索树中// 1、不在，说明水果第一次出现，则插入<水果, 1>// 2、在，则查找到的结点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret == nullptr){countTree.Insert(str, 1);}else{// 修改valueret->_value++;}
}