秋招面试准备
目录
和为k的子数组:
反转链表
(1)SQL:一共1000件商品,每件商品价格范围在(0,1000)元,编写一个sql,分别求出价格在(0,10),(10,120),(120,1000)的商品的数量。table name:item_tab columns:id,name,desc,price;
算法题:一个人每次最多走m阶台阶,问走n阶台阶一共有多少种走法?(动态规划)
- SQL问题,学生id,课程名,分数。1)找到每门课最大得分的学生id,2)每门课平均分,3)找到每门课没有挂科的学生id
两数相加:
合并两个有序数组:
每日温度:
最小栈:
最大子数组和:
区间合并:
在排序数组中查找元素的第一个和最后一个位置
编辑距离:
最长回文子串
和为k的子数组:
思路:前缀和
核心:一定要先查询次数,再put。
class Solution {public int subarraySum(int[] nums, int k) {int[] n = new int[nums.length];int result = 0;Map<Integer,Integer> map = new HashMap<>();map.put(0,1);for(int i = 0;i<nums.length;i++){if(i>0) n[i] = nums[i]+n[i-1];else n[i] = nums[i];if(map.containsKey(n[i]-k)) result = result+map.get(n[i]-k);map.put(n[i], map.getOrDefault(n[i], 0) + 1);}return result;}
}添加注释版:
class Solution {/*** 计算数组中元素和等于k的连续子数组的数量* @param nums 输入的整数数组* @param k 目标和* @return 满足条件的子数组数量*/public int subarraySum(int[] nums, int k) {// 用于存储前缀和的数组,n[i]表示nums[0..i]的元素和int[] n = new int[nums.length];// 记录满足条件的子数组数量int result = 0;// 哈希表:键为前缀和的值,值为该前缀和出现的次数// 用于快速查找是否存在某个前缀和,以优化时间复杂度Map<Integer, Integer> map = new HashMap<>();// 初始化:前缀和为0的情况出现1次(用于处理子数组从索引0开始的情况)map.put(0, 1);// 遍历数组,计算前缀和并统计符合条件的子数组for (int i = 0; i < nums.length; i++) {// 计算当前位置的前缀和if (i > 0) {// 非第一个元素:当前前缀和 = 前一个前缀和 + 当前元素n[i] = nums[i] + n[i - 1];} else {// 第一个元素:前缀和就是自身n[i] = nums[i];}// 核心逻辑:如果存在前缀和为(n[i] - k),说明从对应位置到当前位置的子数组和为k// 例如:若n[i] = 10, k = 3,则寻找前缀和为7的情况,存在几次就有几个符合条件的子数组if (map.containsKey(n[i] - k)) {result += map.get(n[i] - k);}// 将当前前缀和存入哈希表,更新出现次数map.put(n[i], map.getOrDefault(n[i], 0) + 1);}return result;}
}
岛屿数量
数组中第k小的数
多线程,Spring事务转账
反转链表
206. 反转链表
import java.util.*;class ListNode {int val;ListNode next;ListNode() {}ListNode(int val) { this.val = val; }ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}public class Solution {public ListNode reverseList(ListNode head) {// 处理空链表或单节点链表的情况if (head == null || head.next == null) {return head;}// 初始化指针ListNode cur = head.next; // 当前节点从第二个开始ListNode prev = head; // 前驱节点初始为头节点prev.next = null; // 断开原头节点的连接// 开始反转while (cur != null) {ListNode nextTemp = cur.next; // 保存下一个节点cur.next = prev; // 反转指针prev = cur; // 前移prevcur = nextTemp; // 前移cur}return prev; // 返回新的头节点}// ACM模式输入输出处理public static void main(String[] args) {Scanner sc = new Scanner(System.in);// 读取输入String[] vals = sc.nextLine().split(" ");ListNode dummy = new ListNode(-1);ListNode current = dummy;// 构建链表for (String val : vals) {if (!val.equals("null")) {current.next = new ListNode(Integer.parseInt(val));current = current.next;}}// 反转链表Solution solution = new Solution();ListNode reversedHead = solution.reverseList(dummy.next);// 输出结果while (reversedHead != null) {System.out.print(reversedHead.val + " ");reversedHead = reversedHead.next;}}
}
(1)SQL:一共1000件商品,每件商品价格范围在(0,1000)元,编写一个sql,分别求出价格在(0,10),(10,120),(120,1000)的商品的数量。table name:item_tab columns:id,name,desc,price;
SELECT-- 统计价格在(0,10)区间的商品数量COUNT(CASE WHEN price > 0 AND price < 10 THEN 1 END) AS range_0_10,-- 统计价格在(10,120)区间的商品数量COUNT(CASE WHEN price > 10 AND price < 120 THEN 1 END) AS range_10_120,-- 统计价格在(120,1000)区间的商品数量COUNT(CASE WHEN price > 120 AND price < 1000 THEN 1 END) AS range_120_1000
FROM item_tab;算法题:一个人每次最多走m阶台阶,问走n阶台阶一共有多少种走法?(动态规划)
注意点:但m>=n时记得要限制不能将i-j成负数了。
public class toPaLouTi {public int palouti(int m, int n){//dp[i]表示到第i阶楼梯一共有dp[i]种方法。int[] dp = new int[n+1];dp[1] = 1;dp[0] = 1;for(int i = 2;i<=n;i++){for(int j = 1;j<=m&&i-j>=0;j++){dp[i] += dp[i-j];}}return dp[n];}public static void main(String[] args) {int m = 2;int n = 3;int result = new toPaLouTi().palouti(m,n);System.out.println(result);}
}- SQL问题,学生id,课程名,分数。1)找到每门课最大得分的学生id,2)每门课平均分,3)找到每门课没有挂科的学生id
-- 1) 找到每门课最大得分的学生id(若有并列最高分,会返回所有对应学生id)
WITH max_score_per_course AS (SELECT course_name, MAX(score) AS max_score -- 先计算每门课的最高分FROM student_scoreGROUP BY course_name
)
SELECT s.course_name, s.student_id, s.score AS max_score
FROM student_score s
INNER JOIN max_score_per_course m ON s.course_name = m.course_name AND s.score = m.max_score;-- 2) 每门课的平均分(保留两位小数)
SELECT course_name, ROUND(AVG(score), 2) AS avg_score -- 计算平均分并保留两位小数
FROM student_score
GROUP BY course_name;-- 3) 找到每门课没有挂科的学生id(假设60分及以上为及格)
SELECT course_name, student_id,score
FROM student_score
WHERE score >= 60 -- 筛选及格的学生
ORDER BY course_name, student_id;SELECT course_name,student_id,score AS max_score
FROM (-- 子查询中用窗口函数标记每门课的最高分SELECT course_name,student_id,score,-- 按课程分组,给每组的最高分标记为1RANK() OVER (PARTITION BY course_name ORDER BY score DESC) AS score_rankFROM student_score
) AS ranked_scores
-- 筛选出每门课排名第一的学生(包含并列最高分)
WHERE score_rank = 1;
算法问题,简单考察了双指针,升序数组合并,a了后问我如果k路数组合并怎么做,答用归并的思路,然后引导我如果用堆呢,堆里维护每个数组的一个数,然后每次取堆顶即可
手撕:多线程,生产者,消费者
spring事务转账
数组中第k小的数
判断链表是否为回文结构
两数相加:
2. 两数相加
核心是模拟正常加法运算,注意链表之间的链接。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode dummy = new ListNode(0);ListNode cur = dummy;int carry = 0;while(l1!=null||l2!=null){int n1 = l1!=null?l1.val:0;int n2 = l2!=null?l2.val:0;int sum = n1+n2+carry;cur.next = new ListNode(sum%10);cur = cur.next;carry = sum/10;if(l1!=null) l1 = l1.next;if(l2!=null) l2 = l2.next;}if(carry!=0) cur.next =new ListNode(carry);return dummy.next;//使用头节点// ListNode dummy = null;// ListNode cur= dummy;// int carry=0;// while(l1!=null||l2!=null){// int n1 = l1!=null?l1.val:0;// int n2 = l2!=null?l2.val:0;// int sum = n1+n2+carry;// if(dummy==null){// dummy = cur = new ListNode(sum%10);// }else{// cur.next = new ListNode(sum%10);// cur = cur.next;// }// carry = sum/10;// if(l1!=null) l1 = l1.next;// if(l2!=null) l2 = l2.next;// }// if(carry!=0) cur.next = new ListNode(carry);// return dummy;}
}//没有使用虚拟头节点需要单独处理头节点合并两个有序数组:
88. 合并两个有序数组
核心:nums1本身已经预留了,合并的位置,所以这里只要保证从后往前修改就不会修改掉nums1本身的值,循环截止条件是j>=0,这里表示的是只要把所有nums2的数据都插入nums1的时候循环结束,但nums1的所有数据都比nums2大的时候,直接进入else部分把nums2的数据都插入nums1就行。
class Solution {public void merge(int[] nums1, int m, int[] nums2, int n) {int i = m-1;int j = n-1;int k = m+n-1;while(j>=0){if(i>=0&&nums1[i]>nums2[j]){nums1[k] = nums1[i];k--;i--;}else{nums1[k] = nums2[j];k--;j--;}}}
}每日温度:
739. 每日温度
核心:使用一个递减栈实现,它结果数据的存入不是在遍历当前元素存入当前元素的结果,是在碰到下一个需要入栈的元素的时候存入的,这就是递减栈的设计巧妙之处。
栈里存的是递减元素的下标。
class Solution {public int[] dailyTemperatures(int[] temperatures) {Stack<Integer> st = new Stack<>();int[] result = new int[temperatures.length];for(int i = 0;i<temperatures.length;i++){while(!st.isEmpty()&&temperatures[i]>temperatures[st.peek()]){int pre = st.pop();result[pre] = i-pre;}st.add(i);}return result;}
}最小栈:
155. 最小栈
思路:维护两个栈,一个栈维护最小元素,栈顶永远是最小元素,只需要在入栈判断是不是比现有栈顶元素小以及出栈判断一下是不是出栈最小元素就可以了。
class MinStack {Stack<Integer> stack;Stack<Integer> min_stack;public MinStack() {stack = new Stack<>();min_stack = new Stack<>();}public void push(int val) {if(min_stack.isEmpty()||val<=min_stack.peek()){min_stack.push(val);}stack.push(val);}public void pop() {if(stack.peek().equals(min_stack.peek())){min_stack.pop();}stack.pop();}public int top() {return stack.peek();}public int getMin() {return min_stack.peek();}
}/*** Your MinStack object will be instantiated and called as such:* MinStack obj = new MinStack();* obj.push(val);* obj.pop();* int param_3 = obj.top();* int param_4 = obj.getMin();*/最大子数组和:
核心点:判断应该判断的时候dp[i-1]的值是否大于0,而不是nums[i]是否大于0,dp【i-1】如果本身就小于0,说明前面的就是累赘,不应该加上前面的,应该子数组从当前值开始算起。
class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];//以当前元素为结尾的连续子数组的最大和dp[0] = nums[0];for(int i = 1;i<nums.length;i++){if(dp[i-1]>0){dp[i] = dp[i-1]+nums[i];}else{dp[i] = nums[i];}}int result = nums[0];for(int i = 0;i<dp.length;i++){result = Math.max(result,dp[i]);}return result;}
}区间合并:
56. 合并区间
思路:先把所有的区间按每个区间的第一个数进行排序,排序结束后,在list中存储当前已经处理好的区间,每到遍历一个新区间,判断该新区间的起始值和list中最后一个区间的终止值的大小,若小于等于,则对比两个区间的终止值哪个大,哪个就是新区间的终止值(在这一步两个区间就合并了),若大于则说明两个区间没有交集。
class Solution {public int[][] merge(int[][] intervals) {List<int[]> result = new ArrayList<>();Arrays.sort(intervals,(a,b)->a[0]-b[0]);for(int i = 0;i<intervals.length;i++){if(!result.isEmpty()){if(intervals[i][0]<=result.get(result.size()-1)[1]){result.get(result.size()-1)[1] = Math.max(intervals[i][1],result.get(result.size()-1)[1]);}else{result.add(intervals[i]);}}else{result.add(intervals[i]);}}return result.toArray(new int[result.size()][]);}
}34. 在排序数组中查找元素的第一个和最后一个位置
在排序数组中查找元素的第一个和最后一个位置
解法一:暴力解法:
class Solution {public int[] searchRange(int[] nums, int target) {List<Integer> index = new ArrayList<>();for(int i =0;i<nums.length;i++){if(nums[i] == target){index.add(i);}}int[] result = new int[]{-1,-1};if(!index.isEmpty()){result[0] = index.get(0);result[1] = index.get(index.size()-1);}return result;}
}解法二:
编辑距离:
72. 编辑距离
思路:首先把三个基本操作定义下来,从一个到另外一个字符串,无非就是增删改
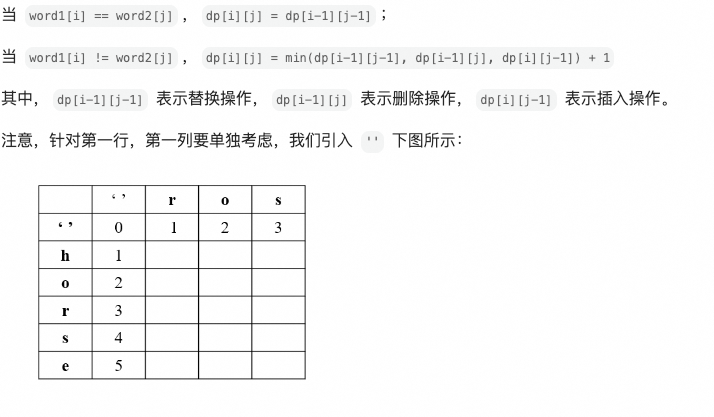
class Solution {public int minDistance(String word1, String word2) {int[][] dp = new int[word1.length()+1][word2.length()+1];//dp数组定义:word1前i个字母和word2前j个字母一致,最短需要操作的次数。// 第一行for (int j = 1; j <= word2.length(); j++) dp[0][j] = dp[0][j - 1] + 1;// 第一列for (int i = 1; i <= word1.length(); i++) dp[i][0] = dp[i - 1][0] + 1;for(int i = 1;i<=word1.length();i++){for(int j = 1;j<=word2.length();j++){if(word1.charAt(i-1)==word2.charAt(j-1)) dp[i][j] = dp[i-1][j-1];else{dp[i][j] =Math.min(Math.min(dp[i-1][j-1],dp[i][j-1]),dp[i-1][j]) +1;}}}return dp[word1.length()][word2.length()];}
}最长回文子串
5. 最长回文子串
思路:要考虑中心节点是一个还是两个
class Solution {public String longestPalindrome(String s) {int max = 1;int start = 0;int end = 0;boolean[][] dp = new boolean[s.length()][s.length()];//i到j之间是否回文字符串for(int r = 1;r<s.length();r++){for(int l = 0;l<r;l++){if(s.charAt(l)==s.charAt(r)&&(r-l<=2||dp[l+1][r-1])){dp[l][r] = true;if(r-l+1>max){max = r-l+1;start = l;end = r;}}}}return s.substring(start,end+1);}
}