机器学习入门，支持向量机

原理简介

支持向量机寻找一个最优超平面来分隔不同类别的数据，目标是最大化边界（margin）——即超平面到最近数据点的距离。

场景：客户信用评分

● 问题描述：银行需要根据客户的收入（特征1）和负债（特征2）判断其信用等级（高风险/低风险）。
● 数据特点：
● 线性可分：客户数据分布存在明显分离边界（如 make_blobs 生成的两簇数据）。
● 小样本：数据量较小（100 个样本），适合 SVM 的小样本优势。

● 适用性：
●SVM 的线性核（kernel=‘linear’）适合低维且线性可分的数据。
● 若特征维度较高（如文本分类），可改用 RBF 核（kernel=‘rbf’）。

代码适配性

● 特征映射：X[:, 0] 和 X[:, 1] 可替换为客户收入和负债的标准化值。
● 标签映射：y 表示信用等级（0=高风险，1=低风险）。
● 输出结果：模型可预测新客户的信用等级，并通过决策边界直观展示风险分界。

模块化代码

将代码拆分为独立函数，提升可读性和复用性：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 1. 数据生成
def generate_data(n_samples=100, centers=2, cluster_std=1.0, random_state=42):X, y = datasets.make_blobs(n_samples=n_samples, centers=centers,cluster_std=cluster_std, random_state=random_state)return X, y# 2. 数据划分
def split_data(X, y, test_size=0.2, random_state=42):return train_test_split(X, y, test_size=test_size, random_state=random_state)# 3. 模型训练
def train_svm(X_train, y_train, kernel='linear', C=1.0):model = SVC(kernel=kernel, C=C)model.fit(X_train, y_train)return model# 4. 模型评估
def evaluate_model(model, X_test, y_test):y_pred = model.predict(X_test)accuracy = accuracy_score(y_test, y_pred)print(f"SVM 准确率: {accuracy:.2f}")return y_pred, accuracy# 5. 可视化结果
def plot_svm_result(X, y, model):plt.figure(figsize=(10, 6))plt.rcParams['font.sans-serif'] = ['Hiragino Sans GB']  # 指定默认字体为黑体plt.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示为方块的问题# 绘制数据点plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', s=50, alpha=0.8)# 创建网格绘制决策边界ax = plt.gca()xlim = ax.get_xlim()ylim = ax.get_ylim()xx = np.linspace(xlim[0], xlim[1], 30)yy = np.linspace(ylim[0], ylim[1], 30)YY, XX = np.meshgrid(yy, xx)xy = np.vstack([XX.ravel(), YY.ravel()]).TZ = model.decision_function(xy).reshape(XX.shape)# 绘制决策边界和间隔ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1],alpha=0.5, linestyles=['--', '-', '--'])# 标记支持向量ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1],s=100, linewidth=1, facecolors='none', edgecolors='k')plt.title('SVM 分类结果 (支持向量已圈出)')plt.xlabel('特征1')plt.ylabel('特征2')plt.show()# 主程序
def main():# 数据生成X, y = generate_data()# 数据划分X_train, X_test, y_train, y_test = split_data(X, y)# 模型训练svm_model = train_svm(X_train, y_train)# 模型评估y_pred, accuracy = evaluate_model(svm_model, X_test, y_test)# 可视化plot_svm_result(X, y, svm_model)if __name__ == "__main__":main()

代码结果

SVM 准确率: 1.00

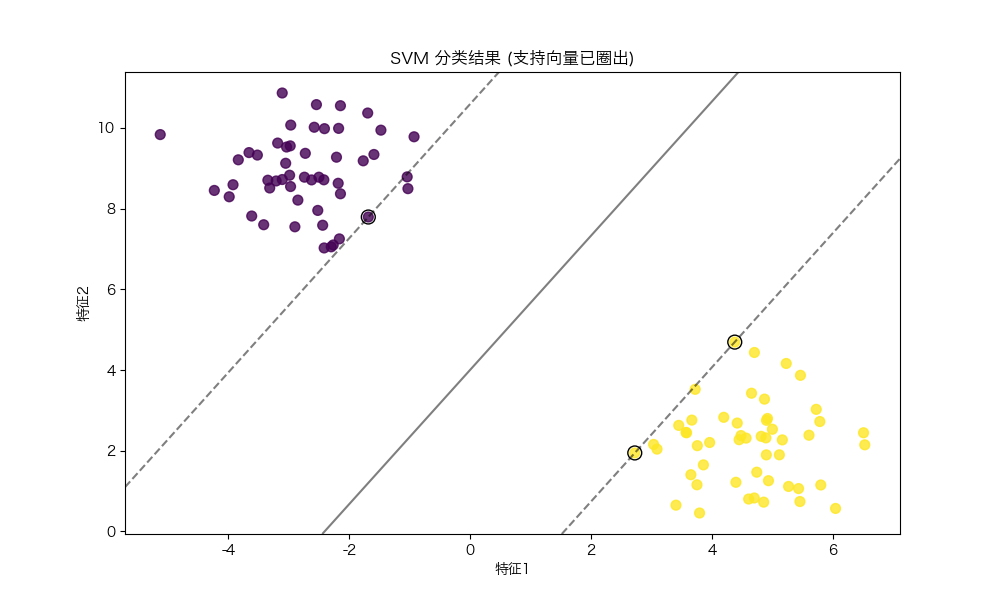
附加说明

准确率公式

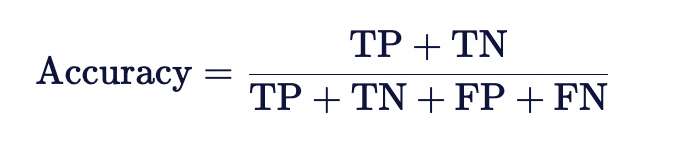
其中：
TP（True Positive）：正类预测为正类（正确）。
TN（True Negative）：负类预测为负类（正确）。
FP（False Positive）：负类预测为正类（错误）。
FN（False Negative）：正类预测为负类（错误）。

计算准确率

方法1：依托现成函数

上述代码中的计算准确率使用的是现成的方法：
accuracy = accuracy_score(y_test, y_pred)

方法2：手工计算

● 对比预测值与真实值：

pythoncorrect = sum(y_pred == y_test)  # 正确预测的数量
total = len(y_test)              # 总样本数

● 计算准确率：

pythonaccuracy = correct / total