力扣hot100:除自身以外数组的乘积(除法思路和左右前缀乘积)(238)
大二课程反而更多了,前两天都没怎么学,这几天补上
题目描述
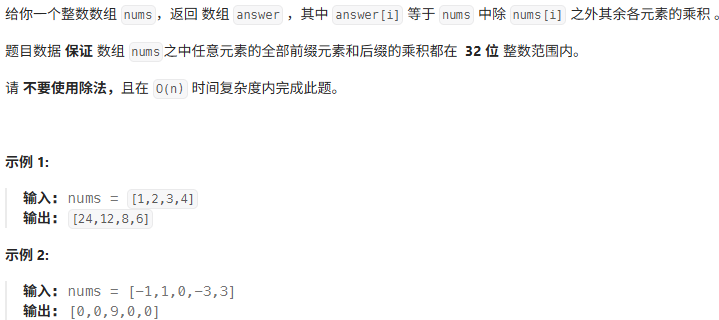
初始思路:利用除法(不符合题目要求)
我最初的想法是先计算所有非零元素的乘积,再根据数组中零的个数分情况处理:
统计零的个数 遍历数组,计算非零元素的乘积
sum,并统计零的个数zero_count。分情况处理:
- 零的个数 > 1:所有结果均为 0。
- 零的个数 = 1:只有零元素的位置结果为
sum,其余为 0。 - 没有零:每个位置的结果为
总乘积 / 当前元素。
public class productExceptSelf {public int[] productExceptSelf(int[] nums) {int sum=1;int[] result=new int[nums.length];int zero_count=0;for(int i=0;i<nums.length;i++){if(nums[i]!=0) {sum = sum * nums[i];}else{zero_count++;}}if(zero_count>1){for (int i = 0; i < result.length; i++) {result[i]=0;}return result;}if(zero_count==1){for (int i = 0; i < result.length; i++) {if(nums[i]==0){result[i]=sum;}else{result[i]=0;}}return result;} else {for (int i = 0; i < result.length; i++) {if (nums[i] == 0) {result[i] = sum;} else {result[i] = sum / nums[i];}}return result;}}
}缺陷:
- 题目明确要求不能使用除法,此方案不符合要求。
- 除法可能导致精度问题(但本题整数数组可接受)。
- 逻辑分支较多,代码冗余。
优化思路:前缀乘积 + 后缀乘积(完美符合要求)
看了一下官方题解,还是人家名门正统的方法比较合理😂
核心思想:每个位置的结果 = 左侧所有元素的乘积 × 右侧所有元素的乘积。
步骤
计算左侧乘积(从左到右遍历)
- 初始化
res = 1(第一个元素左侧无元素)。 res[i] = res[i-1] * nums[i-1](存储位置i左侧所有元素的乘积)。
- 初始化
计算右侧乘积并更新结果(从右到左遍历)
- 初始化
right = 1(最后一个元素右侧无元素)。 - 遍历时,
res[i] *= right(左侧乘积 × 右侧乘积)。 - 更新
right *= nums[i](将当前元素纳入右侧乘积)。
- 初始化
代码实现
public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] res = new int[n];// 计算左侧乘积res[0] = 1;for (int i = 1; i < n; i++) {res[i] = res[i-1] * nums[i-1];}// 计算右侧乘积并更新结果int right = 1;for (int i = n - 1; i >= 0; i--) {res[i] *= right; // 左侧乘积 × 右侧乘积right *= nums[i]; // 更新右侧乘积}return res;
}示例分析
以 nums = [1, 2, 3, 4] 为例:
左侧乘积计算:
res = 1res = 1 × 1 = 1res = 1 × 2 = 2res = 2 × 3 = 6- 此时
res = [1, 1, 2, 6]
右侧乘积计算(从右到左):
i = 3:right = 1→res = 6 × 1 = 6,更新right = 1 × 4 = 4i = 2:res = 2 × 4 = 8,更新right = 4 × 3 = 12i = 1:res = 1 × 12 = 12,更新right = 12 × 2 = 24i = 0:res = 1 × 24 = 24- 最终结果:
[24, 12, 8, 6]
复杂度分析
- 时间复杂度:O(n)O(n),两次遍历数组。
- 空间复杂度:O(1)O(1)(输出数组不计入)。
优势
- 完全避免除法,符合题目要求。
- 无需处理零的特殊情况:零在乘法中自动将对应位置结果置零。
- 逻辑简洁:仅两次遍历,无复杂分支。
总结
- 初始方案:依赖除法,需处理零的边界情况,不符合题目要求。
- 优化方案:通过 前缀乘积 + 后缀乘积 巧妙避免除法,逻辑清晰且高效。 核心技巧:将问题拆分为左右两部分,利用两次遍历累积结果。遇到类似题目时(如前缀和、累积乘积),此思路可举一反三。
最终推荐代码:
public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] res = new int[n];res[0] = 1;for (int i = 1; i < n; i++) {res[i] = res[i-1] * nums[i-1];}int right = 1;for (int i = n-1; i >= 0; i--) {res[i] *= right;right *= nums[i];}return res;
}