算法打卡第15天

翻转二叉树

（力扣226题)

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

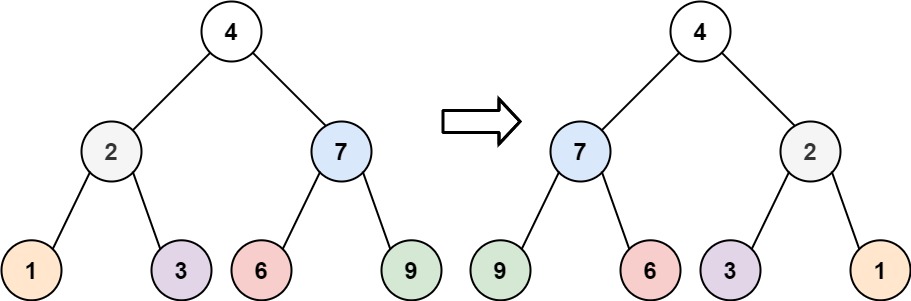
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

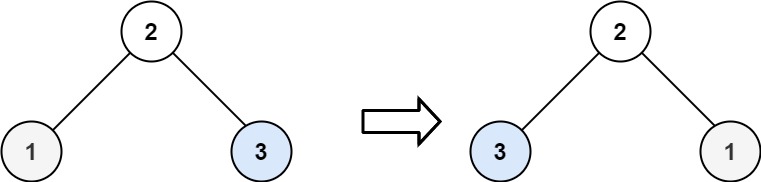
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

解题思路

1. 递归终止条件：如果当前节点为空（root == NULL），直接返回NULL，因为空树的翻转仍然是空树。
2. 交换左右子树：对于非空节点，交换其左右子树。这是通过swap(root->left, root->right)实现的，是翻转的核心操作。
3. 递归处理子树：递归调用invertTree函数分别翻转当前节点的左子树和右子树。由于左右子树已经交换，递归调用实际上是翻转交换后的左右子树。
4. 返回根节点：递归完成后，返回根节点root，此时整棵树已经完成翻转。

这种方法利用递归的思想，从根节点开始逐层翻转二叉树的左右子树，简洁高效。递归的终止条件保证了对空节点的正确处理，而交换操作和递归调用确保了整棵树的翻转。

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {// 终止条件if(root == NULL){return  root;}// 交换当前节点的左右子树swap(root->left, root->right);// 递归invertTree(root->left);invertTree(root->right);return root;}};

对称二叉树

（力扣101题)

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

**进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

解题思路

1. 递归比较函数：定义一个辅助函数 compare，用于递归比较两棵树是否镜像对称。
2. 处理空节点情况：
   • 如果一个节点为空而另一个不为空，直接返回 false，因为不对称。
   • 如果两个节点都为空，返回 true，因为空树是对称的。
3. 处理非空节点：
   • 如果两个节点的值不相等，返回 false。
   • 如果值相等，递归比较左子树的左节点与右子树的右节点（外层），以及左子树的右节点与右子树的左节点（内层）。
4. 递归逻辑：通过递归调用 compare 函数，逐层比较两棵树的对应节点是否满足对称条件。
5. 主函数：在 isSymmetric 函数中，首先判断根节点是否为空。如果为空，直接返回 true。否则，调用 compare 函数比较根节点的左子树和右子树是否对称。

这种方法利用递归的思想，从根节点的左右子树开始，逐层递归比较，确保整棵树的对称性。

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/class Solution {
public:// 递归bool compare(TreeNode *left, TreeNode *right){// 首先排除空节点的情况if(left != NULL && right == NULL)    return false;else if(left == NULL && right != NULL)    return false;else  if(left == NULL && right == NULL)    return true;// 排除了空节点，再排除数值不相同的情况else if(left->val != right->val)      return false;// 此时就是：左右节点都不为空，且数值相同的情况// 此时才做递归，做下一层的判断bool outside = compare(left->left, right->right); // 外层循环 左子树：左、 右子树：右bool intside = compare(left->right, right->left); // 内层循环 左子树：右、 右子树：左bool isSame = outside && intside;return isSame;}bool isSymmetric(TreeNode* root) {if(root == NULL){return true;}return compare(root->left, root->right);}
};

二叉树的 最大深度

（力扣104题)

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

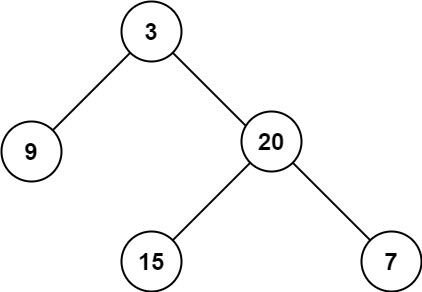
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

解题思路

1. 递归函数：定义一个辅助函数 getheight，用于递归计算二叉树的高度。
2. 递归终止条件：如果当前节点为空（root == NULL），返回高度为 0，因为空树的高度为 0。
3. 递归计算左右子树高度：
   • 递归计算左子树的高度 leftHeight。
   • 递归计算右子树的高度 rightHeight。
4. 计算当前节点的高度：当前节点的高度等于左右子树高度的最大值加 1（max(leftHeight, rightHeight) + 1）。
5. 返回结果：在主函数 maxDepth 中，直接调用 getheight 函数，返回根节点的高度，即二叉树的最大深度。

这种方法利用递归的思想，通过后序遍历（先计算左右子树高度，再计算当前节点高度）的方式，自底向上计算二叉树的最大深度，简洁高效。

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution 
{
public:int getheight(TreeNode* root) // 递归 使用后序遍历{// 因为根节点的高度就是而二叉树的深度  求根节点的高度使用后序遍历因为if(root == NULL)     return 0;//左孩子的高度int leftHeight = getheight(root->left);//右孩子的高度int rightHeight = getheight(root->right);int depth = max(leftHeight, rightHeight) + 1;return  depth;}int maxDepth(TreeNode* root) {return getheight(root);}};

二叉树的最小深度

（力扣111题)

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

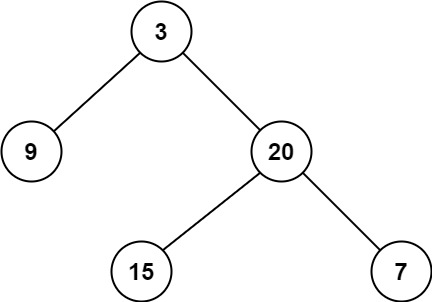
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 [0, 105] 内
• -1000 <= Node.val <= 1000

解题思路

1. 递归终止条件：如果当前节点为空（node == NULL），返回深度为 0，因为空树的深度为 0。
2. 处理特殊情况：
   • 如果左子树为空而右子树不为空，返回右子树的深度加 1。这是因为最小深度是从根节点到最近的叶子节点的距离，此时不能通过左子树计算。
   • 如果右子树为空而左子树不为空，返回左子树的深度加 1，同理。
3. 正常情况：如果左右子树都存在，取左右子树深度的较小值加 1，作为当前节点的最小深度。
4. 递归计算：通过递归分别计算左右子树的深度，然后根据上述规则确定当前节点的最小深度。
5. 返回结果：在主函数 minDepth 中，调用辅助函数 getDepth，返回根节点的最小深度。

这种方法利用递归的思想，通过分别处理左右子树为空和都存在的不同情况，确保能够正确计算二叉树的最小深度

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{
public:int getDepth(TreeNode *node){// 递归终止条件if (node == NULL)return 0;//左子树的深度int leftDepth = getDepth(node->left);// 右子树的深度int rightDepth = getDepth(node->right);// 根节点// 当一个左子树为空，右不为空，这时并不是最低点if (node->left == NULL && node->right != NULL){return rightDepth + 1;}// 当一个右子树为空，左不为空，这时并不是最低点if (node->left != NULL && node->right == NULL){return leftDepth + 1;}// 如果是左右子树都存在,取最小的int result = min(leftDepth, rightDepth) + 1;return result;}int minDepth(TreeNode* root){return getDepth( root);}
};