当前位置：首页 > news >正文

Graph Neural Network(GNN)

news 2025/6/8 9:45:48

我们首先要了解什么是图,图是由节点和边组成的,边的不一样也导致节点的不同(参考化学有机分子中的碳原子)

gnn可以处理classification的问题,也就是分类的问题

也可以处理generation的问题

借一部日剧来说明,这个日剧是讲主角寻找杀害他父亲的凶手的,剧中的人物有姓名和特征

假如我们已经有一些label,我们知道谁肯定不是凶手,将这些人的信息丢进model中,训练model

但是,这是不够的,每个角色的关系也是非常重要的

不过,我们想要运用gnn也有一些难点,我们怎么理顺每个节点间的关系,考虑全局的情况,当这个图变得很大的时候,我们怎么处理,如果我们不知道全部的label,我们该怎么办

我们怎么用已知label的node?我们知道相连的节点间肯定存在着不为人知的关系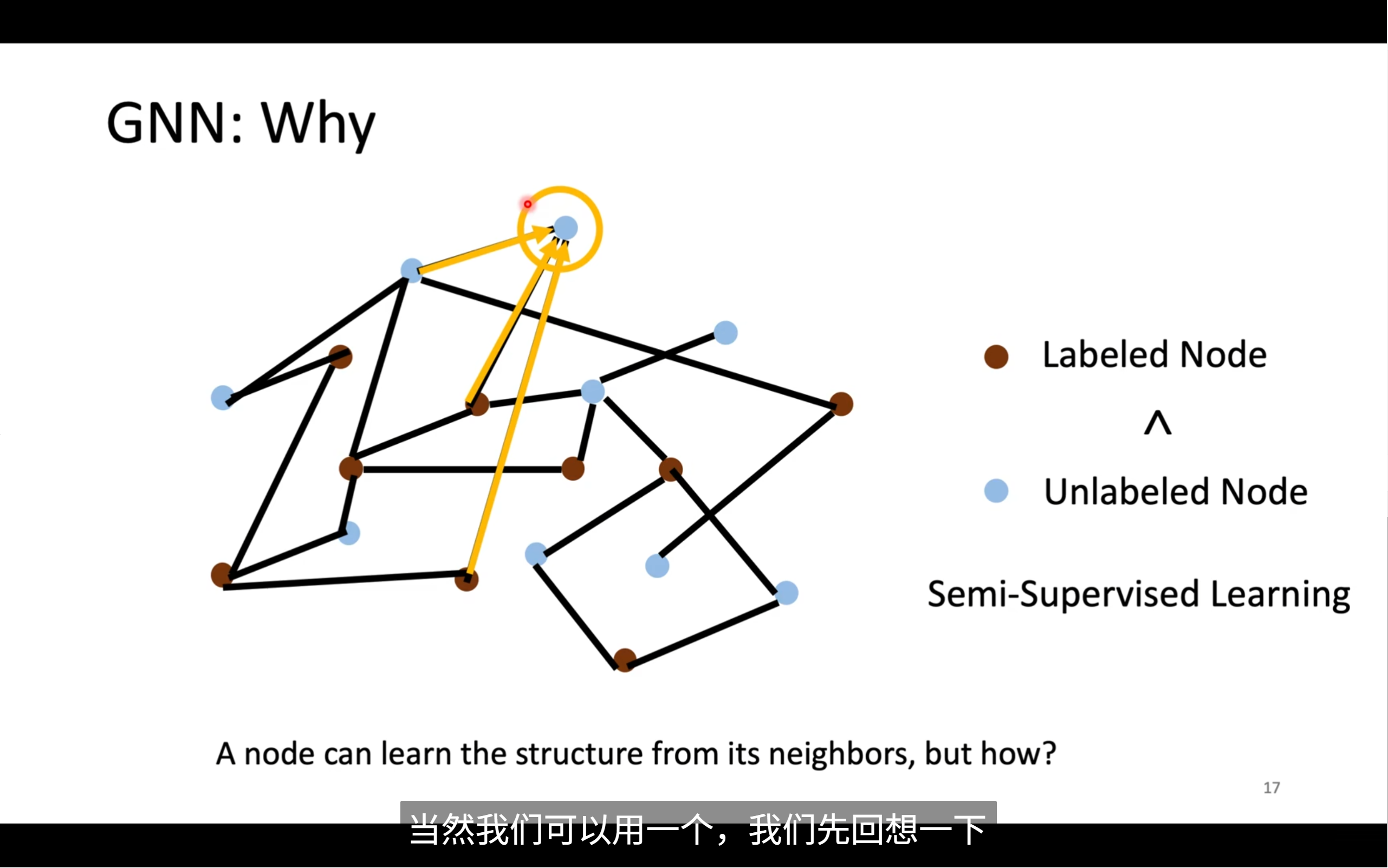

我们在cnn中知道我们做convolution使用卷积核在图像上移动,通过相乘相加来得到一个kernel在区域内的值,也就是feature map,我们该如何将这个方法运用到gnn中呢?

首先来看convolution

🧭 图谱：GNN Roadmap 总览

这张图从四个角度总结了 GNN 的发展路线：

🟨 1. 核心机制：Convolution（图卷积）

GNN 的核心思想是：“将神经网络中的卷积思想迁移到图结构中”，对图中节点进行了特征聚合。

图卷积方法大致分为两类：

Spatial-based（空间域方法）：从节点邻接结构出发，直接对邻居节点进行特征聚合
Spectral-based（频谱域方法）：基于图拉普拉斯分解引入傅里叶变换处理图信号

🧩 2. 空间基 GNN（Spatial-based）

空间方法模拟“邻居信息汇总”的过程，主要体现在不同的 Aggregation（聚合）策略 和对应方法：

Aggregation 类型	示例方法
Sum（求和）	NN4G（Neural Network for Graphs）
Mean（平均汇总）	DCNN, DGC, GraphSAGE
Weighted sum（加权求和）	MoNet, GAT（Graph Attention Network）, GIN（Graph Isomorphism Network）
LSTM 聚合（带门控）	GraphSAGE（使用 LSTM 聚合邻居）
Max Pooling（取邻居最大值）	GraphSAGE

🧠 特别说明：

GraphSAGE 是一个灵活框架，支持多种聚合方式（Mean / LSTM / Pooling 等）
GAT 使用注意力机制决定各个邻居对当前节点的“权重”
GIN 是表达能力最强的空间方法之一，理论上能判别最多非同构图

🟧 3. 频谱基 GNN（Spectral-based）

频谱方法的核心来自图信号处理，先用图拉普拉斯矩阵对图进行谱分解，再定义“卷积”。

主要发展路线如下：

ChebNet → GCN → HyperGCN

ChebNet：使用切比雪夫多项式逼近图滤波器（更高阶）
GCN（Graph Convolutional Network）：最经典的频谱 GNN，使用局部一阶逼近，简洁高效
HyperGCN：将 GCN 推广到超图结构

🎯 频谱方法优点是理论扎实，缺点是需要固定图结构，难以泛化到新图。

🧩 4. 任务（Tasks）：GNN常见应用方向

GNN 强大的表达能力使其适用于多种图数据学习任务：

Supervised Classification：图节点/图整体的分类任务
Semi-supervised Learning：只给部分节点打标签，GNN可以利用邻居信息传播标签
Representation Learning：学习节点/图的表示，如 Graph Contrastive Learning（Graph InfoMax）
Generation：生成新的图结构，如：
- GraphVAE（基于 VAE 的图生成）
- MolGAN（生成分子结构）

🔵 5. GNN 与 NLP 的结合（底部蓝色部分）

“Application: Natural Language Processing”

GNN 在 NLP 中表现出强大的建模能力，因为语言中的很多结构天然可以表示为图：

NLP结构	如何构图
句法依存分析	构建句法依存图（词作为节点，依存关系作为边）
知识图谱	实体为节点，关系为边，一种典型异构图
文档建模	构建“文档-词”或者“词-词共现图”
QA系统	通过 GNN 做 reasoning，对知识路径建模
文本生成	用 GNN 学习长文本逻辑结构关系

经典方法如：

Text GCN
Heterogeneous GNN
GAT for tokens

🧠 图中提到两种理论分析方法：

🔶 顶部橙色部分提到了：

Theoretical analysis: GIN, GCN

说明：

GCN：频谱理论代表作，奠定 GNN 理论的基础
GIN：理论上能判别大多数图的结构，表达能力最强

因此两者处于理论分析的重要位置。

✅ 总结：这张图告诉我们什么？

部分	内容	说明
💛 中间黄色	GNN 的核心机制是图卷积（Spatial vs Spectral）
🟫 棕色框	Spatial 里的不同聚合策略和实例方法
🟧 桃色框	Spectral 的发展脉络（ChebNet → GCN → HyperGCN）
✅ 绿色框	GNN 支持的主要 AI 任务
🔵 蓝色框	GNN 在 NLP 中的重要应用方向

把convolution用在graph上有个区别,就是kernel原本是一个固定大小的kernel,但是图中的kernel是根据节点的edge来变的,只会跟节点的邻居有关

🧠 一、什么是 NN4G？

NN4G（Neural Network for Graphs） 是最早将神经网络的思想用在图结构数据上的一种方法。提出于 2009 年（论文链接见图上），核心思想是：

通过多层感知机（MLP）的形式，把一个节点的邻居特征栈起来输入虚拟“神经元”，合成高层表达。

它可以看作 GNN 的雏形 💡，是图神经网络的鼻祖之一。

🧮 二、整体结构解析

图中展示了图神经网络在某一节点 ( v_3 ) 上的前向传播过程，分为三层结构：

🔸 Input Layer（输入层）

节点表示如下所示，每个节点都有一个特征向量 ( \mathbf{x}_i )，比如：

x₀, x₁, x₂, x₃, x₄

其中 x₃ 是我们关注的节点 ( v₃ ) 的原始输入特征。

🔹 Hidden Layer 0（隐藏层0）

对每个节点 ( v_i )，定义其在第0层的隐藏表示为： [ h_i^0 = \text{MLP}_0(x_i) ] 图中蓝色框表示 ( h_0^0, h_2^0, h_4^0 ) 是节点 ( v_3 ) 的邻居在第0层的表示，红色圆框圈出了这些邻居节点。

这种在图中根据边连接找邻居、获取邻居表示的操作，叫做：

邻居特征聚合（Neighborhood Aggregation）

🔸 Hidden Layer 1（隐藏层1）

要生成节点 ( v_3 ) 的下一层表示 ( h_3^1 )，它由 两部分信息组合而成：

📐 三、关键公式讲解（图右上角）：

[ h_3^1 = \widehat{W}_{1,0} \cdot (h_0^0 + h_2^0 + h_4^0) + \widehat{W}_1 \cdot x_3 ]

我们来逐块解释：

🟩 ① 聚合邻居的隐藏表示总和：

[ (h_0^0 + h_2^0 + h_4^0) ] 代表节点 ( v_3 ) 的所有邻居节点在 Hidden layer 0 的表示。

黄色点表示邻居节点
红色圈出了邻接节点
蓝框内是节点隐藏表示

🟩 ② 聚合邻居后，乘以线性变换：

[ \widehat{W}_{1,0} \cdot ( \cdots ) ] 是一个可学习权重矩阵，对邻居的聚合信息进行线性变换，类似于传统神经网络的 W·x

🟨 ③ 加上自身特征变换：

[

\widehat{W}_1 \cdot x_3 ] 也对节点本身的原始输入特征做一次映射

✨ 整体理解：

“隐藏层新的状态 = 聚合邻居表征 + 本节点特征处理”

这个思想已经是现代 GNN 的共识，后来很多流行 GNN（GCN、GAT、GIN）都在这基础上进行优化：

模型	提升方向
GCN	用归一化、简化计算，变成矩阵形式
GAT	通过注意力机制为不同邻居赋予不同权重
GraphSAGE	把聚合策略做成模块化（mean, max, LSTM 等）
GIN	理论上最强，有最大表达能力

🧭 图中标注说明

图中元素	含义
🟫 棕色节点 `v₀ ~ v₄`	图中的节点
🟨 黄色框 `x_i`	节点在输入层的原始特征向量
🔵 蓝色框 `h_i^0`	节点在第0层的隐藏层表示（由输入计算得出）
🟥 红色椭圆	当前节点 ( v₃ ) 的邻居集合（准备聚合）
🟨+🟩 相加权公式	封装了新的表示生成逻辑

🔍 用一句话来总结 NN4G：

NN4G 是将图结构信息引入神经网络最原始的方式 —— 它通过“邻居求和 + 自身特征”的线性方式来构建节点的逐层表示。

✅ 后续你可以深入的方向：

手动实现 NN4G 的更新函数（用 PyTorch）
比较 NN4G 和 GCN 的异同
用小图跑一遍 Forward Pass
引入非线性/Attention/归一化，看看体验提升

readout是怎么做的呢?

📌 类比记忆（便于理解）

你可以把整个过程想象成一个投票系统，每一层节点像一组专家：

第0层：只知道自己和邻居，局部看问题
第1层：知道两跳关系，有一定全局视角
第2层：更深，能看懂更多上下文

最终，我让三组专家都说一句话，然后用自己设定的权重，综合判断这个图怎么分类。

省略了两个model,接下来的是用weighted sum方法的model,因为每个node的重要性是不一样的,所以会有权重

🧠 MoNet 的核心思想是什么？

MoNet 是一种可以适配不同图结构的通用图神经网络。相比传统 GCN 的**“平均邻居表示”**，它做了两个关键改进：

✅ 1. 给每个邻居一个可学习的权重

不再简单平均！而是根据邻居与中心节点的相对结构关系计算权重。

✅ 2. 使用伪坐标 (pseudo-coordinates) 来定义邻居之间的关系

🧩 图中公式的逐步讲解

✅1. 聚合操作（核心公式）

我们以节点 3 的更新公式（图右上）为例：

h₃¹ = w(û₃,₀) · h₀⁰ + w(û₃,₂) · h₂⁰ + w(û₃,₄) · h₄⁰

说明：

h₃¹：节点 3 在第 1 层的表示
h₀⁰, h₂⁰, h₄⁰：第 0 层时，节点 0、2、4 的表示（邻居们）
w(û₃,₀)：邻接权重（表示节点 3 和节点 0 的关系，由神经网络计算）
·：向量加权
所有邻居的表示都乘上权重后求和，等价于带权聚合

这是一个加权求和（weighted sum）动作，但权重由“距离函数”学习得到。

✅2. 什么是 `ûₓ,y`？

MoNet 的权重函数是作用在“伪坐标”上的。这个伪坐标为：

u(x, y) = [ 1/√deg(x),   1/√deg(y) ]

说明：

deg(x)：节点 x 的度（邻居数量）
所以它是一个 2 维向量，代表了边 (x, y) 两个点的局部结构情况

举例： 如果：

节点 3 度数是 3
节点 0 度数是 2

那么：

u(3, 0) = [1/√3, 1/√2]

然后我们通过一个变换函数（比如一个 MLP）变成：

û₃,₀ = f(u(3, 0))   → 输入伪坐标，输出用于计算权重

✅3. 权重函数怎么定义？

MoNet 使用一种高斯核 + 神经网络的方法来定义权重，右下角的公式是核心：

Σ₍y ∈ N(x)₎  ∑ⱼ  e^(-0.5 · (û(x,y) - μⱼ)ᵀ Σⱼ⁻¹ (û(x,y) - μⱼ)) · fⱼ(h_y)

我们拆解它：

û(x,y)：x 和 y 之间的伪坐标（高维）
μⱼ：某个核中心（高斯分布中心）
Σⱼ：核的协方差矩阵
fⱼ(h_y)：对邻居节点 y 的表示的映射（例如一个MLP）
最外层累加：将不同核的加权结果叠加

✅解释起来像什么？

它就是在说：

“我把相邻节点 y 拿来，把它的距离（û）投给多个高斯核，然后根据这个概率来做加权，决定它对中心节点 x 的影响程度。”

🎨 图示解读补充（连图一起复习）

🔵 图中的内容含义总结：

图中符号	含义
`h₀⁰`（蓝色方块）	节点 0 在 0 层时的特征
`h₃¹`（橙色方块）	节点 3 在 1 层的特征（正在更新）
`u₃,₀`	节点 3 与节点 0 的边的伪坐标
`w(û₃,₀)`	神经网络作用在伪坐标上的输出权重
黄色点	是节点 3 的邻居

✅ 总结 MoNet 的核心逻辑

步骤	描述
① 定义伪坐标 `u(x,y)`	利用节点度数、位置等，描述结构关系
② 定义权重函数 `w(û)`	可以用神经网络对 `û` 建模
③ 加权聚合邻居特征	权重 × 特征后求和，更新中心节点表示

✅ MoNet 的优势

优势	说明
✔️ 通用性强	可应用于图结构、网格、点云等
✔️ 表达能力强	可学习的连续权重模型更细腻
✔️ 包含多个 GNN 的特例	特定情况下它可以约简成 GCN、GAT 等

GAT是对每一个节点的邻居做attention,它的weight是自己学出来的,来分辨邻居对他的重要性

GIN

📌 MLP 是什么？

MLP 全称是：Multi-Layer Perceptron，即 多层感知机，是最基础也是最重要的一种神经网络结构。

✅ 在 GNN/GNN 中，MLP 是个模块/函数：

它的作用是：

把一个向量（比如节点的聚合特征）作为输入，经过若干层 线性变换 + 激活函数，生成新的节点表示。

可以简单表示为：

[ \text{MLP}(x) = \sigma(W_2 \cdot \sigma(W_1 \cdot x + b_1) + b_2) ]

x：输入的向量
W_1, W_2：权重矩阵
b_1, b_2：偏置项
σ：激活函数（通常是 ReLU）

🧠 在 GIN 的公式中 MLP 的具体作用

首先看 GIN 的聚合和更新公式（图上方）：

[ h_v^{(k)} = \text{MLP}^{(k)}\left( (1 + \epsilon^{(k)}) \cdot h_v^{(k-1)} + \sum_{u \in \mathcal{N}(v)} h_u^{(k-1)} \right) ]

我们逐部分拆开解释：

✅ 1. 聚合（邻居加和值）

[ \sum_{u \in \mathcal{N}(v)} h_u^{(k-1)} ]

意思是：把节点 v 的邻居 u 的特征向量都加起来，不做平均、不做权重。

这是 GIN 的创新——使用 sum 聚合，对表示能力更强！

✅ 2. 加上自己的残差：

[ (1 + \epsilon^{(k)}) \cdot h_v^{(k-1)} ]

这里的 ε 是一个可学习的参数（或固定为 0/1），用于控制保留多少“自己的信息”。

✅ 3. 输入 MLP 做非线性映射：

[ \text{MLP}^{(k)}( \cdots ) ]

这一步才是真正更新后的节点表示 h_v^{(k)}，它相当于把“原始 + 邻居特征的整合结果”映射到新空间中。

每一层的 MLP 可以是独立的（拥有自己的一组参数），如下用 PyTorch 实现：

# 输入维度 d_in，隐藏层 2 层，每层都有 ReLU 激活 import torch.nn as nn mlp = nn.Sequential( nn.Linear(d_in, hidden), nn.ReLU(), nn.Linear(hidden, d_out) )

🏗 举个例子形象理解

你可以把 GIN 中的 MLP 理解为下面这个过程：

你聚合邻居说话内容（特征向量加在一起）
加点你自己的声音（残差）
然后这些内容交给一个“智能变压器”——MLP
这个变压器帮你重新加工，变成新的一种表达（下一层特征）

🥇 为什么 GIN 要用 MLP？

作者（Xu et al., 2018）证明：

只有这样一套设计（sum 聚合 + MLP 映射）才能拥有和 Weisfeiler-Lehman(Graph Isomorphism Test) 一样强的判别能力！

✅ 总结

关键词	含义
MLP	Multi-Layer Perceptron，多层感知机
作用	对聚合后的节点特征做非线性映射，提升模型表达能力
在 GIN 中的地位	必不可少，核心结构
与 GCN/GAT 不同	GCN 用线性映射，GIN 用 MLP 所以更强表达性

以上都是spatial based的convolution的方法,下面讲的是很神奇的spectral based的方法

📘 Spectral-Based Convolution（频谱图卷积）- 通俗解析版

🔍 1. 什么是频谱图卷积？

在图神经网络中，频谱卷积（Spectral Convolution） 是一种用“频率”视角来处理图上节点特征的方法。

它的核心思想是：

把图上的节点特征信号变换到频域，在频率维度做滤波，再重新变回来。

这与音频处理中的傅里叶变换非常相似。

🧠 2. 整体流程梳理

我们假设图的一层节点特征是：

Layer i: h0, h1, h2, h3, h4 -> 原始节点的向量特征

我们用以下步骤来“做图卷积”：

步骤 1：Graph Fourier Transform（图傅里叶变换）

输入节点特征 h 转换为“频率分量”
可以想象你提取出：高频信息（变化剧烈），低频信息（平滑）

步骤 2：频域乘以 Filter（滤波器）

这个滤波器决定保留哪些频率信号（就像音频强调低音/高音）

步骤 3：Inverse Transform（逆变换）

把滤波后的频率信息还原回原始节点空间
得到新的节点特征 h'

📐 3. 对于一个图，怎么操作呢？

3.1 构造图的 Laplacian 矩阵

图的拉普拉斯矩阵 L 定义如下：

L = D - A

或者使用归一化形式：

L = I - D^(-1/2) × A × D^(-1/2)

其中：

A 是邻接矩阵（谁和谁有边）
D 是度矩阵（每个节点连接了几个点）
I 是单位矩阵

3.2 做特征值分解（Eigen Decomposition）

对拉普拉斯矩阵 L 分解成：

L = U × Λ × U^T

含义如下：

U 是一组正交向量矩阵（“频率基底”）
Λ 是一个对角矩阵，表示每个频率的强度

可以想象 U 类似于图片/音频信号中的“正弦波模式”。

3.3 图傅里叶变换

用 U 把节点特征 h 转换到频域：

h_hat = U^T × h

h_hat 是每个频率分量对应的权重。

3.4 应用滤波器

我们设计一个频率滤波器 g，用它乘以谱域表示：

h_hat_filtered = g(Λ) × h_hat

这个乘法会对某些频率加强、某些频率减弱（比如保留低频）。

3.5 逆变换回去

最后，我们把经过滤波的频率信号变回节点特征：

h' = U × h_hat_filtered

这个 h' 就是 Layer i+1 层的新节点表示。

💬 4. 总结一下图中的流程

图中展示了从一层到下一层的过程：

Layer i (蓝色) → Layer i+1 (橙色) ↓ ↑ Graph Fourier Transform Inverse Transform ↓ ↑ 频率域表示 × 滤波器（例如一个 3x3 矩阵权值）

这就是频谱法进行图卷积操作的完整流程。

✅ 5. 优点 & 缺点对比

项目	优点 ✅	缺点 ❌
理论基础	来源于图信号处理系统，数学严谨	直观性差，不容易解释
滤波能力	可以严格控制信息流（高频 / 低频）	滤波器是全局的，对“局部邻居”不敏感
适用范围	在小图、固定结构图上表现很好	不支持动态图 / 新图泛化
计算成本	原理上是可控的频率分析	拉普拉斯分解需要 O(n³)，不能用于大图

✨ 6. 衍生版本（简化频谱 GNN 的方法）

由于原始谱卷积太复杂，下面这些方法是对它的高效版本改进：

模型	思想
ChebNet	用多项式（切比雪夫多项式）来“近似滤波器”，提升效率
GCN（Kipf）	截断到一阶近似，变成邻居平均的操作，计算极快、效果稳定

🔚 总结金句

Spectral-based GNN 是一种用“频域滤波”思想来设计图卷积的方式，它继承了信号处理的经典理论，但实际应用中通常会转化为简化形式（如 GCN）。

我们进一步理解图傅里叶变换

✨ 目标：用“生活语言”+ 形象解释，带你读懂图傅里叶卷积的构建砖块！

🧩 一、傅里叶变换到底是什么？

✅ 类比：语音中的“高频”和“低频”

想象你听一段音乐，有低音（鼓声），有高音（小提琴），它们叠加起来构成整段音乐。

傅里叶变换的本质就是：

把一个复杂“信号”（比如音乐）分解成很多纯粹的“频率波”相加得到的结果。

我们用一个“频率眼镜🔍”来观察信号里的结构，看它“包含了哪些高低音”。

✅ 数字信号里也一样

假设你有个连续点的信号：

信号：1 1 1 1 0 0 0 0

一看就是有“变化”
傅里叶变换会说：
- 它包含一个低频分量（因为左边四个一样）
- 有一个边缘突然变化 → 含高频信号

所以：傅里叶变换 ≈ 用振动图告诉你一个东西是平还是抖

✅ 拓展到“图”上怎么办呢？

普通傅里叶变换处理的是连续音频波形
→ 图就像复杂的结构化信号，它是离散但有连边（结构）

我们想知道：

图上节点的特征变化是“光滑”的，还是“很震荡”的？

于是我们对“图上的信号”（比如节点特征）也想做傅里叶分析，那就用下面这些数学工具！

📘 二、度矩阵 D 是什么？

非常简单！

对于每个节点来说，它连接了几个邻居？

我们称这个数量为“度数”Deg。

节点	邻居	度数
A	B, C	2
B	A, C, D	3
C	A, B	2

我们会构造一个对角矩阵 D，比如上面的图会变成：

D = 
[2, 0, 0]
[0, 3, 0]
[0, 0, 2]

行列都是节点
对角元素就是“每个节点的连边数”
非对角部分全是 0 ✅

📘 三、邻接矩阵 A 是什么？

邻接矩阵就是：

如果两个节点有边连接，填 1
没连接就是 0

A =
[0 1 1]
[1 0 1]
[1 1 0]

这个结构就表示“谁和谁连着”，矩阵视角下的图结构。

📘 四、拉普拉斯矩阵 L 是什么？

图的核心符号来了！

我们用度矩阵 D 和邻接矩阵 A 构造出一个矩阵 L：

L = D - A

也就是说：

自己度数（连边多少） → 放在对角线
去掉其他连接关系 → 做差

它本质上是——

惩罚“你和邻居差太多”的一个矩阵！

✅ 举个具体例子：

D = [2, 0, 0] [0, 3, 0] [0, 0, 2] A = [0 1 1] [1 0 1] [1 1 0] ⇒ L = D - A = [ 2 -1 -1 ] [-1 3 -1 ] [-1 -1 2 ]

这个矩阵是图傅里叶分析的灵魂！

🧠 五、特征值分解（Eigen Decomposition）是啥？

你可以理解为：

把矩阵抽象成很多“方向 + 伸缩量”的集合

像把物体旋转 → 拆解成“每个方向上”是什么形状。

对于矩阵来说，分解成：

L = U × Λ × U^T

含义是：

U：图的“频率基底”，像音频里的“正弦波”
Λ：每个频率的权重 = 频率“强度”
U^T：还原回原始空间的方法

U^T × h：就是“把节点特征投影到频率空间”
Λ × （这个h）：就是“滤波”
U × (...) ：是把频率信息还原成节点结构

✅ 六、整套流程顺口溜（保姆级）：

💬 一句话：

图 → 构造邻接矩阵 A 和度矩阵 D
得到拉普拉斯矩阵 L = D - A
分解得到频率基底：U，Λ
把节点特征 h 变到频率空间：U^T × h
滤波器作用：乘 Λ 或 g(Λ)
再变回来：U × 上一步 → 得到 h'

✅ 七、总结一句话！

概念	通俗理解
度矩阵 D	每个节点有几个朋友？
邻接矩阵 A	谁和谁是朋友？
拉普拉斯矩阵 L	你和邻居之间的“差异衡量”
特征分解	把图的频率结构提取出来
傅里叶变换	看哪些点“震荡得多”

再具体讲解一下邻接矩阵是怎么表示节点间关系的

📘 什么是邻接矩阵（Adjacency Matrix）？

邻接矩阵用于表示图中有哪些节点连在一起。是一个二维矩阵，每一行和每一列都对应同一个节点。

✅ 举个图的例子

假设我们有一个很简单的无向图，它有 4 个节点，编号为 0、1、2、3，并且结构如下：

图结构： (0) / \ (1)-(2) | (3)

连接边是：

节点 0 连着节点 1、2
节点 1 连着节点 0 和 2
节点 2 连着节点 0、1、3
节点 3 连着节点 2

🧱 它的邻接矩阵 A 是：

我们创建一个 4×4 的矩阵，行列都代表节点编号。

0 1 2 3 ← 列（目标节点） A = [ ← 行（源节点） [ 0 1 1 0 ], # 节点0连了1和2 [ 1 0 1 0 ], # 节点1连了0和2 [ 1 1 0 1 ], # 节点2连了0,1,3 [ 0 0 1 0 ] # 节点3只连了2 ]

🔎 如何看这个矩阵？

你可以这样记住：

A[i][j] = 1 表示节点 i 和 j 有连边
A[i][j] = 0 表示 i 和 j 没有连边

比如：

A[0][1] = 1 → 节点 0 连了节点 1 ✅
A[3][0] = 0 → 节点 3 没连节点 0 ❌
A[2][3] = 1 → 节点 2 连了节点 3 ✅

因为图是无向图，所以邻接矩阵是对称的！

🧠 那“节点的特征表示”数据在哪？

题问得非常好！邻接矩阵 只负责表示“结构”，
节点真正的 数值特征表示是什么，是另外一个矩阵 (X) —— 节点特征矩阵！

假设我们给每个节点一个特征向量

节点 0: 特征 = [1.0, 0.2] 节点 1: 特征 = [0.9, 0.1] 节点 2: 特征 = [0.3, 0.8] 节点 3: 特征 = [0.2, 0.5]

我们写成矩阵：

X = [ [1.0, 0.2], # 节点 0 [0.9, 0.1], # 节点 1 [0.3, 0.8], # 节点 2 [0.2, 0.5] # 节点 3 ]

也就是说：

每一行是一个节点的特征
列表示这个特征的维度（可以是 2 维、5 维、100 维都行）

🔁 在 GNN 中我们怎么用这些？

在图神经网络里，我们常常做的是：

用邻接矩阵 A 来“指导”节点之间互相传递表示（特征）

结构来源于 A（谁影响谁）
特征来源于 X（每个节点自身内容，比如文本、图像等）

✅ 用最简单的代码说明

使用 PyTorch 简化说明：

import torch # 邻接矩阵 A（4个节点） A = torch.tensor([ [0, 1, 1, 0], [1, 0, 1, 0], [1, 1, 0, 1], [0, 0, 1, 0] ], dtype=torch.float32) # 节点特征 X（每个节点是2维向量） X = torch.tensor([ [1.0, 0.2], # 节点 0 [0.9, 0.1], # 节点 1 [0.3, 0.8], # 节点 2 [0.2, 0.5], # 节点 3 ]) # 简单的图卷积核心思想：A @ X output = A @ X print(output)

你会发现，它就是用邻接矩阵，把邻居特征“加”过来了！

🏁 最后一句话总结：

对象	表示什么
邻接矩阵 A	表示图结构：谁和谁相连
特征矩阵 X	表示节点内容（如每个节点标题、颜色、向量等）
A × X	就是用结构去聚合邻居的节点特征（最基本 GCN 核心）

进一步理解傅里叶变换

📘 一、傅里叶变换的第一性问题：它想干啥？

用一句话说：

傅里叶变换（Fourier Transform）就是把你身边“复杂的信号”分解成一组“简洁的正弦波”来表达。

原始信号可能又高又低、快慢不一，看起来很复杂
傅里叶告诉我们：其实所有的复杂波形都可以看作一个个**“纯频率的波”**叠加得到

🎵 举个通俗例子（一听就懂）：

你听一段音乐，感觉很复杂：

有小提琴 → 高频
有大鼓 → 低频
有人声 → 中频

你听不出哪些部分有啥，但傅里叶变换可以“分析”出来每种频率分量有多强。

📊 二、从信号图像看傅里叶

🔶 假设你有这样一个函数：

f(t) = 一段起伏变化的信号（比如语音、电压、气温序列）

它是关于时间 t 的函数，如下图（想象）：

     ^
f(t) |            (¯¯¯)      (¯)|         (¯¯)    (__)|    (___)+--------------------------→ t

你看它好像乱七八糟，但其实：

✅ 傅里叶告诉你：

这个 f(t)，其实是若干个不同频率的正弦/余弦波叠加出来的！

也就是说：

f(t) ≈ a₁·cos(w₁·t) + a₂·cos(w₂·t) + a₃·sin(w₃·t) + ...

每个 cos(w·t) 是一段波（频率为 w）
a 是振幅，表示这个频率有多强
全部加在一起，就变成原始函数！

🔍 三、那傅里叶“变换”到底是什么？

傅里叶“变换”是个运算符号，它把函数从 “时间/空间域” 转换到 “频率域”。

✅ 数学表达：

如果：

f(t) 是一个实数函数

则它的傅里叶变换 F(ω) 定义为：

F(ω) = ∫( -∞ 到 ∞ ) f(t) · e^(-iωt) dt

解释：

这是一个“投影”的过程，把 f(t) 投到复指数 (e^{-iωt}) 上
相当于问：“在频率 ω 这一波上，有多少存在？”
得到所有 ω 对应的“存在感”后，就得到了频域表达 (F(ω))

🧠 概念翻译（不讲复杂积分）：

🔁 还有逆变换！

你也能从频率分量“还原”原图：

f(t) = ∫( -∞ 到 ∞ ) F(ω) · e^(iωt) dω

✨ 四、傅里叶变换的几种直观“视角”

角度	描述
🎶 声音分析	从时域变频域，看哪些音高（频率）最强
📷 图像压缩	看哪些空间频率信息最有用
🌊 信号滤波	把高频噪音滤掉，保留低频“主体结构”
⚙️ 系统模拟	看一个系统是对哪些频率响应强（滤波器响应）

✅ 五、小例子：你真想试一试傅里叶变换的效果？

用 Python（仅 5 行代码！）看看频域长啥样：

import numpy as np import matplotlib.pyplot as plt t = np.linspace(0, 1, 1000) signal = np.sin(2 * np.pi * 5 * t) + 0.5 * np.sin(2 * np.pi * 20 * t) freq = np.fft.fftfreq(len(t), t[1] - t[0]) fft_result = np.fft.fft(signal) plt.plot(freq[:500], np.abs(fft_result)[:500]) plt.title("频率分布图") plt.xlabel("频率(Hz)") plt.ylabel("振幅") plt.show()

你会看到两个频率上有峰值：5Hz 和 20Hz，说明信号来自这两个振动！

🧠 总结（一句话背下来）：

傅里叶变换就是把一个信号分解成频率的组合，把“混音”变成“频谱”，就像给嗓音做频率分析一样！

✅ 你现在知道的：

名词	通俗解释
时域 (f(t))	就是原始数据随时间变化的样子
频域 (F(ω))	就是告诉你“有哪些频率组成了这个信号”
傅里叶变换	从时域 → 频域
逆变换	从频域 → 时域
正弦/余弦波	就是最基本的高频/低频振动单位，傅里叶的“积木”

在信号与系统中,当然,也在数学中

我们用合成与分析来进行傅里叶变换

📘 N-dim Vector Space（N维向量空间）

🌟 一、这张图讲的是什么？

这张图讨论的是：

在一个 N 维空间中，任何向量（A）都可以表示为一组“基底”的加权和。

就像：你可以用“【上下】【左右】”这两个方向，来表示地图上的任意一点。

✅ 图中三个公式解释如下：

🟢 1️⃣ 合成公式（构建一个向量）

A = ∑(k = 1 到 N) [ a_k × v̂_k ]

翻译成中文：

向量 A 是由 N 个基底向量 v_k，乘上它们各自的系数 a_k，最后加起来组成的。我们称这组 v_k 是一组“基底（basis）”。

🔸 举个例子（二维）：

A = [3, 4]  
= 3 × [1, 0] + 4 × [0, 1]  
→ 用 x 轴上的单位向量 + y 轴上的单位向量，来合成整个 A。

这就是 “合成”。

🟣 2️⃣ 分析公式（如何计算每个系数）

a_j = A · v̂_j

翻译：

想知道 “A 在第 j 个方向上的强度”，只需要求 A 与第 j 个基底向量的点积。

也就是说：

如果你手上有一个向量
想知道它“在某个方向上有多大分量”
就用点乘（dot product）去计算

🔵 3️⃣ 正交公式（基底之间互不打架）

v̂_i · v̂_j = δ_ij   （δ_ij 是克罗内克δ）

含义：

当 i = j → 点乘结果 = 1
当 i ≠ j → 点乘结果 = 0

这是说：

一组好的基底向量彼此之间是正交的（垂直的），它们互相没有“混叠”，独立纯粹。

这在傅里叶变换中特别重要：

不同频率 = 不同的方向
用一组正交波形（正弦、余弦）来表示所有信号
所以傅里叶基底是“正交基底”

✨ 图中合成 & 分析的对比

概念	对应公式	含义
合成（Synthesis）	A = ∑ a_k · v_k	把基底拼在一起组成向量 A
分析（Analysis）	a_k = A · v_k	把向量 A 拆到每个基底方向上的强度
正交性	v_i · v_j = 0（i ≠ j）	每个方向不会影响另一个方向

🔄 类比到傅里叶变换（连接频域的核心）

向量范畴	傅里叶范畴
向量 A	时域信号 f(t)
基底 vector v_k	正弦波 e^(iωt)（频率基底）
系数 a_k	频率分量 F(ω)
合成公式	f(t) = ∑ F(ω) × e^(iωt)
正交性	正弦/余弦之间也是正交的

🎯 用一张图总结

      ←---------------------------→
时域信号 f(t)     ←→     频域分量 F(ω)合成                              分析⬆️                                   ⬇️∑ a_k·v_k        ←        Dot Product（拼成向量）               （拆分方向强度）

✅ 总结一句话

向量空间中的“分析”、“合成”思想，就是傅里叶变换的数学基础！

把信号 f(t) 看作一个向量
把频率波形 e^(iωt) 看作一组正交基底
傅里叶变换 = 分析信号“投影到各频率”的大小
傅里叶逆变换 = 合成出完整信号

接下来是

🧠 本页要讲解的是：构建谱图卷积中的图结构数据

🎯 1. 什么是 Graph G = (V, E)

这个是图的基本定义：

V 是图的节点集合（比如人、人、城市）
E 是图的边集合（谁和谁有关系）
N = |V| 表示节点数量，例如有 5 个节点 → N = 5

📦 2. 邻接矩阵 A ∈ ℝⁿˣⁿ

我们用一个矩阵 A 来表示图的结构（也叫权重矩阵、Adjacency Matrix）。

A[i][j] = 边 (i, j) 的权重

图中定义了：

A[i][j] = { 0 如果 i 和 j 之间没边 w(i, j) 如果 i 和 j 之间有边（权重） }

如果是无权图，我们一般写成 1 表示有边
如果是加权图，用 w(i, j) 表示边的权重值

✅ 特别说明：

图中说：

We only consider undirected graphs

也就是说：

A[i][j] = A[j][i]
邻接矩阵是对称的！

🔢 3. 度矩阵 D ∈ ℝⁿˣⁿ

Degree Matrix，表示的是每个节点“有几个邻居”。

D[i][i] = d(i) = 节点 i 的度数（跟几个人连接） D[i][j] = 0 如果 i ≠ j （非对角线全 0）

也就是说：

度矩阵是一个对角矩阵，每个对角线元素的值等于该节点的度数（即 A 的每一行之和）

✅ 公式解释：

D[i][j] = { d(i), 如果 i == j （对角线） 0, 否则 }

你可以把它想象成：

D = diag([度数0, 度数1, ..., 度数N])

📊 4. 图上的信号 f : V → ℝⁿ

这句话特别关键！

把图上的每个节点都赋一个 数值信号（特征）。

比如：

节点 i	f(i) 表示
0	温度 = 25℃
1	文本情感值 = 0.8
2	像素强度 = 135

我们用一个函数：

f : V → ℝ

或者记作一个向量：

f = [f(0), f(1), f(2), ..., f(N-1)]

🔁 🧠 总结一下这页讨论的核心元素

符号	含义
G = (V, E)	图结构（节点 + 边）
N	节点数量
A	邻接矩阵（结构连接关系）
D	度矩阵（每行度数）
f(i)	图上每个节点携带的特征或信号

这些元素是谱图卷积中建模图结构的“数学基础”，后面你就会看到拉普拉斯矩阵、傅里叶变换等都会基于这些计算。

‼️ 后面会涉及的概念预告（帮你衔接理解）：

下一步，我们会使用：

A 和 D 来构造 图拉普拉斯矩阵 L ：L = D - A
然后用 L 做特征分解，做图傅里叶变换
实现图神经网络中的频域卷积（如 ChebNet, GCN 等）

📘 图谱理论中的核心知识点：Graph Laplacian 的光谱分解

✅ 1. 图拉普拉斯矩阵：L = D - A

这是谱方法中最基础的一步：

A 是邻接矩阵，用于表示每对节点之间有没有连边
D 是度矩阵，每个对角线元素是某节点的度（连接数）
L = D − A 被称为非归一化拉普拉斯矩阵

它本质上在做什么？

表示“一个节点和它的邻居有多不一样”的结构度量。

✅ 2. L 是对称矩阵（symmetric）

如果图是 无向的（Undirected Graph），那么 A 是对称的，因此 L = D - A 也是对称矩阵。

对称矩阵有哪些好处？

一定可以被特征值分解
有一组正交的特征向量作为基底

这为后面进行傅里叶变换做铺垫！

✅ 3. 光谱分解：L = U × Λ × Uᵀ

这是最关键的一步，也叫谱分解，或者特征值分解。

你可以把它理解为对这个“图的结构矩阵”进行“频谱分析”。

U 是由 L 的特征向量组成（每一列是一个特征向量）
Λ 是对应的特征值，排成一个对角矩阵（对角线上是 λ）

📌 数学上讲： [ L \cdot u_k = \lambda_k \cdot u_k ] 也就是说：每个 ( u_k ) 是 L 的一个特征向量，对应特征值 ( \lambda_k )

一个特征值 λ_k 对应一个频率

一个特征向量 u_k 就是“这个频率方向上的基底”

✅ 4. 矩阵符号说明

符号	含义
Λ（Lambda）	一个对角矩阵，对角线上是特征值 λ₀, λ₁,...
U	N×N 的矩阵，每一列是 L 的特征向量 ( u_0, u_1, ..., u_{N-1} )
Uᵀ	U 的转置，作为还原操作（就像傅里叶逆变换）
L	拉普拉斯矩阵，通过 U 和 Λ 组合可以还原出来

✅ 5. 可视化解释图（下方彩色方块）

这个图像表达的是：

L = U × Λ × Uᵀ

可以类比如下操作：

复杂图 L → （解构）→ 频率空间（Λ）+ 基底方向（U） → → 再还原回来（Uᵀ）

黄色方块（L）：复杂原始数据（表示节点之间的结构关系）
中间蓝绿蓝（U * Λ * Uᵀ）：对它进行分解为频率分量（Λ），各方向上的响应（U）

🧠 特征值 λ 与“频率”的直觉理解：

λ 小 → 平滑的特征 → 类似于低频（变化不大）
λ 大 → 抖动剧烈的特征 → 类似于高频（变化大）

图傅里叶变换就是：

用 Uᵀ × f 把节点特征投影到这些“频率维度”上，分析其中成分。

📌 最后一行结论

λₗ 是一个特征值（frequency），
uₗ 是它对应的特征向量（frequency direction）

正如：

在普通傅里叶中：频率 = 1Hz, 2Hz, ..., 震动方向 = cos(ωt), sin(ωt)
在图信号中：频率 = λ，振荡模式 = uₗ

📋 总结表格

项目	含义	类比于普通傅里叶中
L	图结构的整体拉普拉斯矩阵	f(t) 的二阶导数结构
U	图的“基底向量”	正弦波 / 复指数函数 e^(iωt)
Λ	图的频率分量（特征值）	各频率大小 ω²
aₖ = Uᵀ · f	投影到频域的系数	Fourier Coefficients

🙋 快问快答（帮你理解更牢）

Q1：为什么我们要做这个分解？

→ 把图信号投影到频率空间上（做滤波、分析）

Q2：为啥 L 可以被这样分解？

→ 因为 L 是实对称矩阵（性质好），所以一定能特征值分解

Q3：U 和傅里叶基底有什么关系？

→ 就是图上的傅里叶基，定义的是“节点之间的振动模式”

就象是这样的

图谱理论

能量差异越大,频率也就越大

💡 图信号的平滑度 (smoothness) 与拉普拉斯算子

这张图解释的是如何通过图拉普拉斯矩阵 L 计算图信号的“抖动程度”或“变化强度”，
也就是《图傅里叶变换》和《图神经网络》中信号处理的基础！

📌 总体目标：

探索图信号在图结构下的“变化程度”：

变化剧烈（高频） → 信号不平滑
差异小（低频） → 信号平滑

最后我们会看到这个关键词：

(1/2) × ∑∑ w_ij × [f(v_i) - f(v_j)]²

它测量了：所有边上两个节点的值差异之“平方和加权平均”——就是图信号的“粗糙程度”。

🧠 我们从第一行开始分解说明：

✅ 第 1 行

(Lf)(vᵢ) = ∑(vⱼ ∈ V) wᵢⱼ · (f(vᵢ) - f(vⱼ))

这表示对于图中的每个节点 (vᵢ)，图拉普拉斯作用在函数 f 上的值，是：

自己和邻居之间的一种加权差值和
( w_{ij} ) 是节点 i 和 j 之间的边权（出自邻接矩阵 A）

从图滤波的角度，它表示“当前节点与邻居节点值的偏差总量”。

✅ 第 2 行：写成整体的矩阵二次型形式

fᵀ·L·f = ∑(vᵢ ∈ V) f(vᵢ) × ∑(vⱼ ∈ V) wᵢⱼ (f(vᵢ) - f(vⱼ))

这是更常见的谱空间内写法，表示的是“信号 f 在结构 L 下的变异度”。

✅ 第 3 行：展开乘法

把每一项的乘法乘进去：

= ∑∑ wᵢⱼ × (f(vᵢ)² - f(vᵢ)·f(vⱼ))

✅ 第 4 行：对称性合并项，乘 (1/2)

这个是技巧，只适用于 无向图（对称情况）：

= 1/2 × ∑∑ wᵢⱼ × [f(vᵢ)² - f(vᵢ)f(vⱼ) + f(vⱼ)² - f(vᵢ)f(vⱼ)]

✅ 第 5 行：最终简化公式⚡️✨

= 1/2 × ∑∑ wᵢⱼ × (f(vᵢ) − f(vⱼ))²

这就是最重要的一步：

⭐ 它表示信号在图结构上的总变化程度（能量）
即：两个连接节点之间，数值差得越多，代表图信号变化剧烈

🧮 通俗总结就是：

图结构上：

如果两点连得近（大 wᵢⱼ）但值差很多 → 惩罚很大
如果两点连得近但值差不多 → 惩罚小

→ 所以这个式子是一个“图信号的光滑度量 / 不一致程度量”。

📊 信号平滑举例：

节点对	f(vi)	f(vj)	差的平方	权重 wᵢⱼ	加权项贡献
A-B	5	5	0	1	0
C-D	5	0	25	1	25

→ smooth 的信号在一条边上变化小，值更小。

🟩 为什么这重要？

在图神经网络中，我们希望：

学到的特征 f 不要在图上乱跳动
它要尽量“随着连接关系而变化平滑”

所以这个公式就非常重要，用来衡量：

GCN 中信息传播的平滑化本质
图傅里叶中滤波器行为
图正则化（Graph Laplacian Regularization）

✅ 数学 vs 直觉总结对照表

符号部分	通俗直觉
fᵀLf	信号在图结构中的粗糙度
(Lf)(vᵢ)	点 vi 的“变化趋势"
∑∑ wᵢⱼ(fᵢ − fⱼ)²	所有“边上差异”的总能量
权重大但值差 → 惩罚大	更不平滑，更高频

✅ 最后一整句话总结

图拉普拉斯作用于信号 f （fᵀLf）衡量了信号在图结构中“跳动”的大小。
它越小，说明信号越平滑，越是沿着图结构自然传播或变化的。

对于这个特征值(λ)和我们的频率之间的关系

✅ 简单一句话：

在谱图理论中，λ 是特征值（eigenvalue），它表示信号在图结构上变化的“幅度”或“频率”。

🧠 图结构中的 λ 是一种“频率尺度”

再多解释一点：

在傅里叶变换中，我们把一个信号（函数）表示为很多不同频率的正弦波的叠加
在图上没有正弦波了，我们用特征向量 uₖ 来代替“频率基”
对应的 λₖ 就是这个“频率基”对应的频率强度

🔍 图中内容逐行讲解

✅ 第一行公式是什么？

公式如下：

uiT⋅L⋅ui=λiuiT⋅L⋅ui=λi

这是标准的特征值定义：

你试图在某个方向 uᵢ 上施加图拉普拉斯变换（L），

看它会乘上一个比例因子多少 —— 这个比例就是 λᵢ。

你可以理解为：

uᵢ：某个“震荡/振动”的方向（图上的基底）
λᵢ：这个振动基底的“频率能量大小”

小 λ ➜ 平滑（低频）

大 λ ➜ 抖动明显（高频）

✅ 第二行英文解释：

The eigenvectors corresponding to small λ belong to the low-pass part of a graph signal.

意思是：

小 λ 对应的特征向量 u 表示的是图信号中“变化较小”（很平滑、低频）的部分。

也就是说——在图上传播得越“顺”，λ 越小；变化越突然（比如两个连的点，值差很大），λ 越大。

📊 表格解释

λ（特征值）	所代表的频率	对应的特征向量 `u`	图中信号示意
λ = 0	最小频率（平滑）	`[0.5, 0.5, 0.5, 0.5]ᵀ`	所有节点值一样（DC 分量）
λ = 1	低频	`[−0.41, 0, −0.41, 0.82]ᵀ`	仅轻微起伏
λ = 3	高频	`[0.71, 0, −0.71, 0]ᵀ`	一端高一端低（变化剧烈）
λ = 4	最高频率	`[−0.29, 0.87, −0.29, −0.29]ᵀ`	中间疯狂震荡（像锯齿）

🔍 图下方图示解释

这些橙色垂直线表示：

每一列 uₖ 是一个长度为节点数的向量，每个数值表示一个节点的“振动强度”

你可以把它想成图上的一个振动模式：

所有 uᵢ 的值一致 → 没有起伏（DC成分）
逐渐变化 → 低频
左右跳跃、正负交替 → 高频

🧠 类比到普通傅里叶

普通傅里叶变换	图傅里叶（谱图理论）
正弦波 sin(ωt)	特征向量 uₖ（图上的“频率波”）
频率 ω₂ > ω₁	特征值 λ₂ > λ₁
频率越高 ✦ 震动越快	λ 越大 → 信号在图上起伏越剧烈

🔚 总结一句话：

λ 是图结构的“频率”，u 是频率的“形状”，f·u 就能得到你的图信号在这个频率方向上有多强。

在图神经网络中，我们常常：

用 λ 控制图卷积要保留“低频”还是“高频”
用 uₖ 来对信号做傅里叶变换
λ 越小 → 表明方向越“平滑”，适合做平滑卷积
λ 越大 → 方向抖动大，感觉像“噪声通道”

🎁 补充图示记忆法 🎨

λ = 0 → －－－（全部一样） λ = 1 → ／＼／＼（起伏轻微） λ = 3 → －v－^－（左右翻转感） λ = N-1 → －^－v^－（变化频繁，高频）

对于这个图傅里叶变换来说

x 是图上每个节点对应的原始特征（信号）
U 是图的“频率基底”（Laplacian 的特征向量矩阵）
x̂ 就是频率空间下的图信号，通过逐个特征向量 uₖ 点乘 x 得到
把 x 投影到各个震荡方向上，得分解强度

每一行：`uₖ · x` 表示什么？

就是图信号在第 k 个频率方向（特征向量 uₖ）上的分量有多强！

对应左边那列紫色标签：

u₀ ⋅ x   → 低频
u₁ ⋅ x   → 中低频
u₂ ⋅ x   → 中高频
u₃ ⋅ x   → 高频（震荡很大）

小 λ 对应的频率低，图信号“平滑”
大 λ 对应的频率高，图信号“变化大”

图傅里叶逆变换：

x=U⋅x^x=U⋅x^

把不同频率方向上的振动强度组合还原，回到原图信号
就是紫色频谱反向合成橙色原始向量

✅ 左下角：（图谱空间 x̂ 的直觉图）

你可以看到横轴是 λ（频率），纵轴是信号 x 在每个频率基 uₖ 上的投影大小：uₖ · f

这张小图就告诉你信号中含有多少“低频”、“高频”成分。

✅ 中下图（图上的原始信号）

在图结构上，每个节点都有一个信号值：

f(v0), f(v1), f(v2), f(v3)

这些就是我们一开始的输入信号向量 x

✅ 右上角（普通傅里叶对比）

上图：

原始波形函数：f(t) 的时间序列
下图：
- 把 f(t) 投影到不同频率之后的频谱图
- 每个向量 aₖ = f(t) 投影到 sin/cos 频率空间上

图傅里叶做的和这个一模一样：

只是把 sin() 替换成 uₖ（特征向量）

🤔 用图上数据做个直觉小例子

假设你图上有 4 个节点：

x = [1, 2, 2, 1]

意思是：

v₀ = 1
v₁ = 2
v₂ = 2
v₃ = 1

这个信号很平滑（中间比边上高），你变换后会看到它在低频 λ₀, λ₁上有很大能量，而在高频 λ₃上没有多少。

✅ 最终总结金句：

图傅里叶变换是把图信号投到“结构频率”的空间，让我们分析它是平滑还是震荡。

这个频率空间是由拉普拉斯矩阵的特征向量 uₖ 决定的，

✅ 图中概念关键词解读：

项目	含义
x	图信号（每个节点的数值）
U	图的特征向量矩阵（频率基底）
x̂	图信号在频率空间下的表达
Uᵀ·x	图傅里叶变换（分析）
U·x̂	图傅里叶逆变换（还原）

然后就是图傅里叶逆变换

我们将频谱中的频率信号乘上一个对角矩阵,也就是机器要去学习的,得到yhead,这就是filter的原理

我们要将频谱中的信号重新转到图信号,所以

最终这个方法可以总结成

但会造成一些问题,比如说对g的选择会影响L,节点的大小也会影响model大小,并不像cnn一样,不管图片是多大,model的大小是一样的,还有第二个问题,比如说g就是cosL,泰勒展开后会有L的N次方

L·x → 融合了一阶邻居
L²·x → 相当于走了 2 步，考虑的是二阶邻居
L³·x → 考虑三阶邻居
...
L^N·x → 所有节点都会影响所有节点（全局信息传递

ChebNet可以解决信号在全局的问题

但这个net的问题在于时间复杂度太高了,那么怎么降低呢,可以用一个递归的函数

然后我们就可以将x替换,得到下图中的式子

进行这个转换的原因是为了让计算简单,就像下面数学题

接下来是数学推导

我们当然可以learn出来几个filter

GCN是最受欢迎的model

L是归一化后地矩阵,最大特征值是2

✅ 最终把整个 GCN 你可以这样理解：

步骤	做了什么
Ã + D̃	处理图结构（谁和谁有边、还包括自己）
归一化	确保邻居平均传播，不影响不同节点度数
H^{(l)} × W	相当于全连接层
σ(...)	激活函数加非线性

🧠 总结记忆：

GCN = 邻居信息平均 + 网络权重投影 + 非线性

✅ GCN 的好处

优点	含义
💡 局部化传播	每一层只看一阶邻居，结构清晰可解释
⚙️ 高效	不需要计算谱分解，没有 UΛUᵀ
💪 可迁移	可以泛化到任意图结构，不固定拉普拉斯