当前位置：首页 > news >正文

最小均方误差（MMSE）滤波器及其改进版

news 2025/5/25 9:15:53

一、最小均方误差（MMSE）滤波器

二、最小均方误差（MMSE）滤波器改进版

自适应滤波器会根据底层像素值改变其基本特性，这使其能够在去除噪声的同时保留图像细节。确定滤波器特性的典型标准涉及局部亮度和对比度的某种度量。我们将探讨两种类型的自适应滤波器：一种使用标准统计量，另一种使用顺序统计量来度量局部变化。

一、最小均方误差（MMSE）滤波器

最小均方误差（MMSE）滤波器是自适应滤波器的一个典型例子，它基于局部图像统计量表现出可变的特性。通过使用一阶和二阶统计量（均值和方差），我们可以获得局部变化的度量：均值衡量局部平均亮度，方差衡量局部对比度。结合噪声方差的先验知识（需要事先知道噪声方差），这两个指标可用于确定滤波器的特性。MMSE 滤波器在处理高斯噪声或均匀噪声时效果最佳，其定义如下：局部均值方差快速计算方法

$MMSE=d(r,c)-\frac{\sigma _{n}^{2}}{\sigma_{l}^{2}}[d(r,c)-m_{l}(r,c)]$

其中： $\sigma _{n}^{2}$ ：为噪声方差；

W：以d(r,c)为中心像素的N*N窗口；

$\sigma _{l}^{2}$ ：局部方差

$m_{l}$ ：局部均值

当图像中没有噪声时，噪声方差等于零，此时该方程将返回未经过滤的原始图像。在图像的背景区域（即原始未损坏图像中像素值相当恒定的区域），噪声方差将等于局部方差，该方程退化为均值滤波器。在图像中局部方差远大于噪声方差的区域，滤波器会返回接近未过滤图像数据的值。这是理想的效果，因为高局部方差意味着高细节（边缘），而自适应滤波器会试图保留原始图像的细节。

一般来说，MMSE 滤波器返回的值由未滤波的图像数据 d (r,c) 组成，其中部分原始值被减去，并添加了部分局部均值。用于修改原始值的原始数据和局部均值的比例由噪声与局部方差的比值 σₙ²/σₗ² 加权决定。随着该比值的增加（表明窗口内主要是噪声），滤波器主要返回局部平均值；当该比值降低（表明局部细节丰富）时，滤波器会更多地返回未滤波的原始图像数据。通过这种方式，MMSE 滤波器能够适应局部图像的统计特性，在去除噪声的同时保留图像细节。如下图展示了 MMSE 滤波器在添加高斯噪声的图像上的应用，其中需要指定窗口（核）大小和噪声方差。

二、最小均方误差（MMSE）滤波器改进版本

改进 MMSE 滤波器效果的一种方法是允许窗口大小根据噪声与局部方差的比值动态调整：

在背景恒定区域，希望使用较大的窗口，使噪声方差和局部方差接近相等，比值尽可能接近 1。在零均值噪声假设下，此时滤波器返回均值以消除更多噪声变化。
在图像细节区域（如边缘），希望使用较小的窗口以仅保留边缘的更多细节。这可以通过从最大窗口大小开始，并对噪声与局部方差的比值设置最小阈值来实现。如果未达到阈值，则减小窗口大小，直至满足阈值或达到最小 3×3 窗口大小。

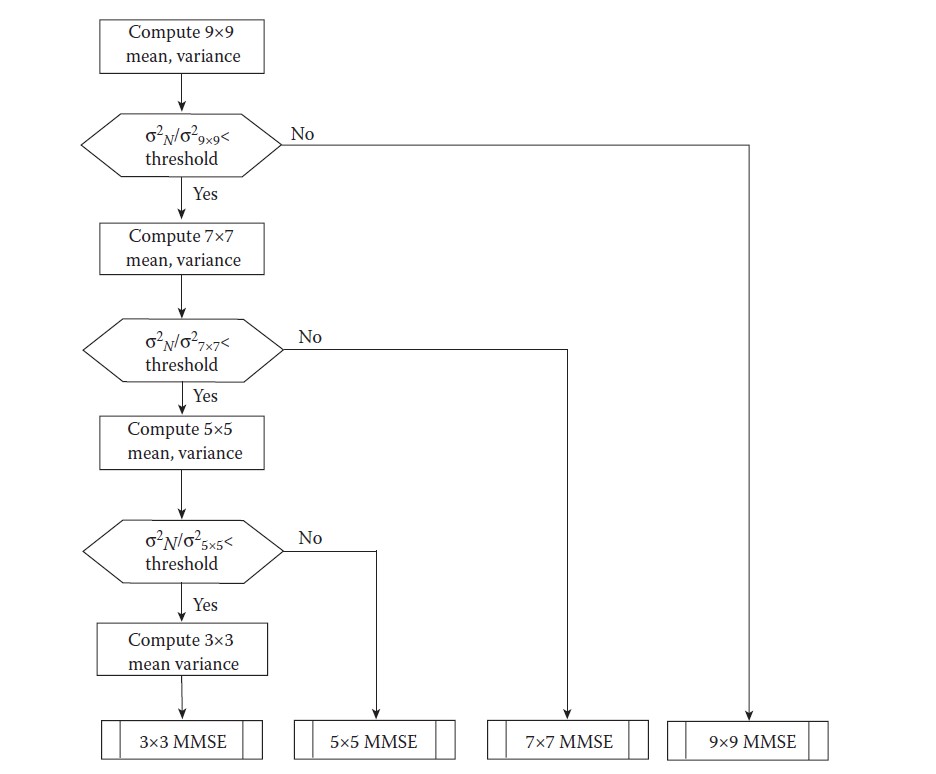
该算法的流程图如下图所示。在这个示例中，算法从 9×9 的最大窗口大小开始：