数据结构与算法——链式二叉树
链式二叉树
- 遍历方式与其规则
- 代码的实现
- 递归的复习
- 前,中,后序遍历的实现
- 二叉树结点个数
- 二叉树叶子结点个数
- 二叉树第k层结点个数
- 二叉树的深度/高度
- 二叉树查找值为x的结点
- 二叉树销毁
- 层序遍历
遍历方式与其规则
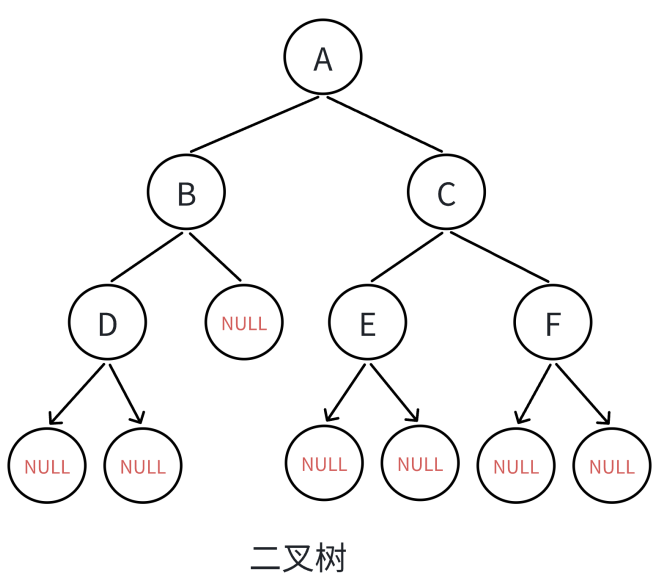
- 前序遍历:访问根结点的操作发⽣在遍历其左右⼦树之前,顺序:根,左,右
- 中序遍历:访问根结点的操作发⽣在遍历其左右⼦树之中(间),顺序:左,根,右
- 后续遍历:访问根结点的操作发⽣在遍历其左右⼦树之后,顺序:左,右,根
代码的实现
递归的复习
递归分为两个阶段,分别是递推与回归,先递推,然后回归。
定义:递归其实是⼀种解决问题的⽅法,在C语⾔中,递归就是函数自己调用自己。
思想:把⼀个⼤型复杂问题层层转化为⼀个与原问题相似,但规模较⼩的⼦问题来求解;直到⼦问题不能再被拆分,递归就结束了。所以递归的思考⽅式就是把⼤事化⼩的过程。
递归的限制条件:
- 递归存在限制条件,当满⾜这个限制条件的时候,递归便不再继续。
- 每次递归调⽤之后越来越接近这个限制条件。
前,中,后序遍历的实现
首先定义链式结构二叉树,然后自己手动构建一个如开始图中的二叉树
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//定义链式结构二叉树
typedef char BTDataType;
typedef struct BinaryTreeNode {BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//申请创建结点空间
BTNode* buyBode(char x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode)); //分配整个结构体的内存if (node == NULL){perror("malloc fail!");exit(1);}node->data = x;node->left = node->right = NULL;return node;
}
//手动创建二叉树
BTNode* creatBT()
{BTNode* nodeA = buyBode('A');BTNode* nodeB = buyBode('B');BTNode* nodeC = buyBode('C');BTNode* nodeD = buyBode('D');BTNode* nodeE = buyBode('E');BTNode* nodeF = buyBode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->left = nodeE;nodeC->right = nodeF;return nodeA;}
- 前序遍历
//前序—根左右
void preOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ",root->data);preOrder(root->left);preOrder(root->right);
}

这里画图理解一下前序遍历递归

- 中序遍历
//中序—左根右
void inOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}inOrder(root->left);printf("%c ",root->data);inOrder(root->right);
}

- 后序遍历
//后序-左右根
void postOrder(BTNode* root)
{if (root == NULL){printf("NULL");return;}inOrder(root->left);inOrder(root->right);printf("%c ", root->data);
}

二叉树结点个数
思路:根节点 + 左子树结点个数 + 右子树结点个数(需要判断根结点是否为空)
//结点个数-非空就+1
int BTNodeSize(BTNode* root)
{if (root == NULL){return 0;}return 1 + BTNodeSize(root->left) + BTNodeSize(root->right);
}


二叉树叶子结点个数
思路:如果根节点为空返回0;如果root的左结点与右结点为空,说明有且仅有root一个结点,返回1;如果都不是返回左子树叶子结点个数+右子树结点个数。
//叶子结点个数——度为0
int BTLeadSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;//有且仅有只有一个结点}return BTLeadSize(root->left) + BTLeadSize(root->right);
}


二叉树第k层结点个数
思路:左子树的第(k-1)层结点个数 + 右子树的第(k-1)层结点个数
//第k层结点个数
int BTLevelSize(BTNode* root,int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BTLevelSize(root->left, k - 1) + BTLevelSize(root->right, k - 1);
}


二叉树的深度/高度
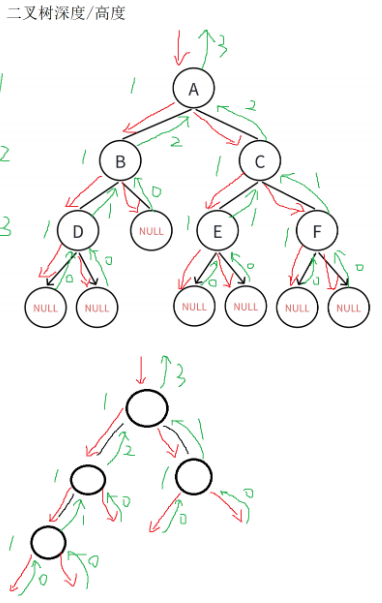
求树中结点的最大层次,根为第一次,往下递增。
思路:根结点+左子树与右子树中最大高度
//求二叉树的高度
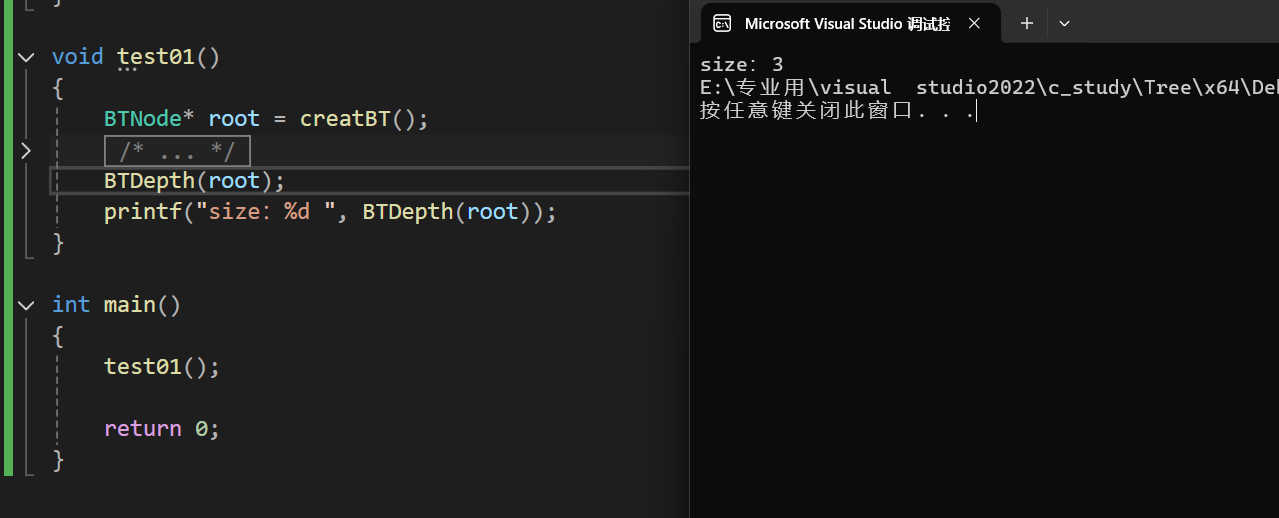
int BTDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDep = BTDepth(root->left);int rightDep = BTDepth(root->right);return 1+(leftDep > rightDep ? leftDep : rightDep);
}
二叉树查找值为x的结点
思路:从根结点开始找,然后查找左子树,左子树查完查右子树,直到查到就返回结束,不用继续查找
//查找二叉树中的值x
BTNode* BTFind(BTNode* root, BTDataType x)
{if (root == NULL){return 0;}if (root->data == x){return root;}BTNode* leftFind = BTFind(root->left, x);if (leftFind){return leftFind;}BTNode* rightFind = BTFind(root->right, x);if (rightFind){return rightFind;}return NULL;
}

二叉树销毁
思路:结点通过遍历一个一个销毁,为了找到每一个结点,所以采用后序遍历从左子树的叶子结点往上销毁,然后从右子树的叶子结点往上销毁。
//二叉树的销毁
void BTDestroy(BTNode** root)
{if (*root == NULL){return 0;}BTDestroy(&(*root)->left);BTDestroy(&(*root)->right);free(*root);*root == NULL;
}
如果只用一级指针 BTNode* root,函数内部可以递归释放所有结点,但外部的 root 指针仍指向已被释放的内存(悬空指针),可能导致程序崩溃或未定义行为。
通过传递 BTNode** root(指针的地址),可以在释放内存后,将外部的 root 指针设为 NULL,彻底消除悬空指针。

层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对⼆叉树进⾏层序遍历。设⼆叉树的根结点所在层数为1,层序遍历就是从所在⼆叉树的根结点出发,⾸先访问第⼀层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,⾃上⽽下,⾃左⾄右逐层访问树的结点的过程就是层序遍历。
实现层序遍历需要额外借助数据结构:队列(先进先出)
队列内存储的类型是二叉树结点的结构
将结点的左右孩子入队列(前提是不为空),只要队列不为空,打印队头


/层序遍历
void leverOrder(BTNode* root)
{Q q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头,出队头BTNode* top = QueueFront(&q);QueuePop(&q);printf("%c ", top->data);//将队头非空左右孩子入队列if (top->left)QueuePush(&q, top->left);if (top->right)QueuePush(&q, top->right);}QueueDestroy(&q);
}
