比较结构的连通性
在行列可自由变换的平面上4点结构有16个
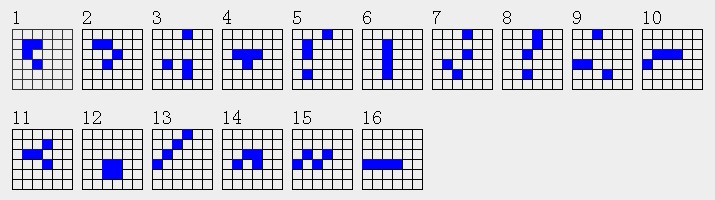
按照连通性可被分成3 种

第一种所有点在横竖方向都可以连在一起
第二种所有点彼此都是独立的,没有相互作用

第三种结构中一部分点是彼此连通的,一部分彼此是独立的,介于前两种之间。
第一种的7个结构显然可以填满整个平面,但是不是所有第一种的结构都可以填满平面?
比较十字结构的连通性

由于十字结构的对称性,在平面上把两个十字组合在一起只有5种可能,第一种和第二种是对称的,所以只有4种情况。
用第一种填充平面

在20*20的平面上有277个点

在30*30的平面上有623个点
| 尺寸 | 总数量 | 点 | 占比 | |
| 20 | 400 | 277 | 0.6925 | |
| 30 | 900 | 623 | 0.692222 | |
| 40 | 1600 | 1108 | 0.6925 | |
| 100 | 10000 | 6923 | 0.6923 | |
| 200 | 40000 | 27692 | 0.6923 |
所以如果平面足够大,用形状1填满整个平面的密度就是9/13=0.6923
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 2 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 7 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 9 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 10 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 11 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 12 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 13 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 14 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 15 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 16 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 17 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 18 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 19 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 20 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
在20*20的矩阵中很直观,这个结构无论是行还是列都是由
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
不断的循环构造的。

用形状2充满整个平面有在20*20的平面上有360个点
其他数据为
| 尺寸 | 总数量 | 点 | 占比 | |
| 20 | 400 | 360 | 0.9 | |
| 30 | 900 | 810 | 0.9 | |
| 50 | 2500 | 2250 | 0.9 | |
| 100 | 10000 | 9000 | 0.9 |
所以形状3的极限密度就是9/10=0.9.

在20*20的平面上形状4有211个点,
其他数据为
| 尺寸 | 总数量 | 点 | 占比 | |
| 20 | 400 | 211 | 0.5275 | |
| 30 | 900 | 476 | 0.52889 | |
| 50 | 2500 | 1324 | 0.5296 | |
| 100 | 10000 | 5294 | 0.5294 |
所以形状4的极限密度是9/17=0.5294

在20*20的平面上,形状5有144个点
| 尺寸 | 总数量 | 点 | 占比 | |
| 20 | 400 | 144 | 0.36 | |
| 30 | 900 | 324 | 0.36 | |
| 50 | 2500 | 900 | 0.36 |
很直观形状5的极限密度就是9/25=0.36
| 密度 | ||
| 1 | 9/13 | 0.69231 |
| 2 | 9/13 | 0.69231 |
| 3 | 9/10 | 0.9 |
| 4 | 9/17 | 0.52941 |
| 5 | 9/25 | 0.36 |
第3种密度最大,第5种密度最小。
显然因为结构1,2由于自带空隙是不可能填满平面的。
所以这意味着在第一种全连通的情况下有两种可能,一种是可以填满整个平面的,一种是不能填满整个平面的。
所以结构按照连通性可以分成4种
| 1 | 全连通,有长程相互作用,可以填满整个平面 | |||||
| 2 | 全连通,有长程相互作用,但不能填满整个平面 | |||||
| 3 | 点与点之间彼此完全独立,没有相互作用 | |||||
| 4 | 介于全连通与完全独立之间 | |||||
