491. 非递减子序列
题目

思路与解法
class Solution:def findSubsequences(self, nums: List[int]) -> List[List[int]]:self.res = []self.path = []self.backtracking(nums, 0)return self.resdef backtracking(self, nums, starIdx:int):if len(self.path) >= 2:self.res.append(self.path[:])i = starIdxused = set()while i < len(nums):if (not self.path or nums[i] >= self.path[-1]) and nums[i] not in used:used.add(nums[i])self.path.append(nums[i])self.backtracking(nums, i+1)self.path.pop()i += 1
46. 全排列
题目
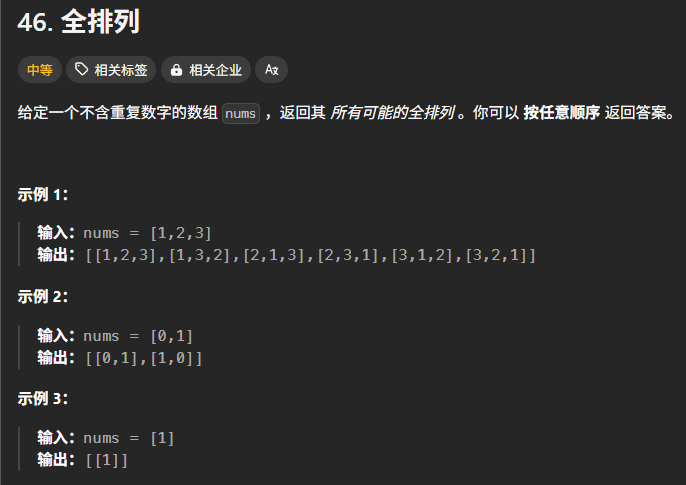
思路与解法
class Solution:def permute(self, nums: List[int]) -> List[List[int]]:self.res = []self.path = []self.backtracking(nums)return self.resdef backtracking(self, nums):if len(self.path) == len(nums):self.res.append(self.path[:])returnfor i in range(len(nums)):if nums[i] not in self.path:self.path.append(nums[i])self.backtracking(nums)self.path.pop()
47. 全排列 II
题目

思路与解法
class Solution:def permuteUnique(self, nums):nums.sort() result = []self.backtracking(nums, [], [False] * len(nums), result)return resultdef backtracking(self, nums, path, used, result):if len(path) == len(nums):result.append(path[:])returnfor i in range(len(nums)):if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]: continueused[i] = Truepath.append(nums[i])self.backtracking(nums, path, used, result)path.pop()used[i] = False



