【力扣刷题记录】hot100错题本(一)
1. 简单题

我的答案:时间复杂度过高:O(N^3)
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:for num in nums:if (target - num) in nums:#多余for i in range(len(nums)):if nums[i] == num :for j in range(i+1,len(nums)):if nums[j] == (target - num) :return [i,j]
官方题解:
#暴力枚举,时间复杂度:O(N^2)
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:n = len(nums)for i in range(n):for j in range(i + 1, n):if nums[i] + nums[j] == target:return [i, j]return []作者:力扣官方题解
链接:https://leetcode.cn/problems/two-sum/solutions/434597/liang-shu-zhi-he-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。#哈希表,时间复杂度:O(N),此时找target - num的时间复杂度变为O(1)
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:hashtable = dict()#创建一个空字典哈希数组,用于存储已经遍历过的数字和她们的索引for i, num in enumerate(nums):#使用 enumerate 同时遍历 nums 中的索引 i 和对应的值 num。if target - num in hashtable:return [hashtable[target - num], i]hashtable[nums[i]] = ireturn []作者:力扣官方题解
链接:https://leetcode.cn/problems/two-sum/solutions/434597/liang-shu-zhi-he-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
2. 中等题

官方题解
#最小堆,堆的时间复杂度是O(log n),故总的时间复杂度为O(nlog n)
#初始时堆为空,将最小丑数1加入堆,每次取出堆顶元素x,x是堆中最小的丑数,则把2X,3X,5X都加入堆,用哈希集去重
class Solution:def nthUglyNumber(self,n: int) -> int:factors = [2,3,5]seen = {1}heap = [1]for i in range(n-1):curr = heapq.heappop(heap) #返回堆中最小元素for factor in factors:if (num := curr * factor) not in seen:seen.add(num)heapq.heappush(heap,num)#将数存入堆中并保存堆的结构return heapq.heappop(heap)
#优先队列,利用三个指针的移动,需要计算丑数数组中的n个数,故时间复杂度为O(n)
class Solution:def nthUglyNumber(self,n: int) -> int:dp = [0]*(n+1)p2 = p3 = p5 =1dp[1] = 1 for i in range(2,n+1):num2,num3,num5 = dp[p2]*2,dp[p3]*3,dp[p5]*5dp[i]=min(num2,num3,num5)if dp[i] == num2:p2+=1 if dp[i] == num3:p3+=1if dp[i] == num5:p5+=1return dp[n]
3. 美团笔试错题

def calculate_alternate_steps():T = int(input()) # 次数for _ in range(T):n = int(input())arr_str = input().strip()arr = [0] + list(map(int, list(arr_str))) # 下标从1开始start = int(input())left_steps = 0right_steps = 0visited = set()current_index = startdirection = 'right' # 初始向右while True:visited.add(current_index)current_value = arr[current_index]next_index = -1if direction == 'right':for i in range(current_index + 1, n + 1):if arr[i] > current_value and i not in visited:next_index = iright_steps += 1breakdirection = 'left' # 切换方向else: # direction == 'left'for i in range(current_index - 1, 0, -1):if arr[i] > current_value and i not in visited:next_index = ileft_steps += 1breakdirection = 'right' # 切换方向if next_index == -1:break # 没找到更大的,停止current_index = next_indexprint(f"{right_steps} {left_steps}")4. 字母异位分词

- 方法一:排序
逻辑:互为异位词的两个字符串包含的字母相同,因此对两个字符串分别进行排序后得到的字符串一定相同,可将排序之后的字符串作为哈希表的键。
时间复杂度:对于每个字符串,需要O(klogk)的时间排序,以及O(1)的时间更新哈希表,有n个字符串,故时间复杂度为O(nklogk),k为字符串的最大长度。
class Solution:def groupAnagrams(self,strs:List[str]) -> List[List[str]]:mp = collections.defaultdict(list) #创建一个默认顺序的哈希表,key是排序后的字符串,value是一个list,存放对应的原始字符串,defaultdict的好处是当key不存在时,自动创造一个空列表,不用手动创建for st in strs:key = "".join(sorted(st))#对字符串进行排序;"".join()表示将()里的重新拼接成一个新的字符串mp[key].append(st)#把字符串加进list中return list(mp.values())
- 方法二:计数
异位的词中各个字母计数也相同,可以将每个字母出现的次数用字符串表示,作为哈希表的键。
时间复杂度: O ( n ( k + ∣ Σ ∣ ) ) O(n(k+|\Sigma|)) O(n(k+∣Σ∣)),n为字符串个数,k为字符串最大长度, ∣ Σ ∣ |\Sigma| ∣Σ∣为字符集长度,此处为26;对于每个字符串,需要对其k个字母进行计数, O ( ∣ Σ ∣ ) O(|\Sigma|) O(∣Σ∣)的时间生成哈希表的键,同时以及O(1)的时间写进哈希表。
##异位的词中各个字母计数也相同,可以将每个字母出现的次数用字符串表示,作为哈希表的键
class Solution:def groupAnagrams(self,strs:List[str]) -> List[List[str]]:mp = collections.defaultdict(list)for st in strs:counts=[0]*26for ch in st:counts[ord(ch) - ord("a")] += 1 #构建了一个列表,将'a'~'z'映射到数组下标0~25,ord(ch)得到字符的ASCII码# 需要将list转换为tuple才能进行哈希,因为list是mutable类型(可变类型),可以将如a=[1,2,3];a[0]=100;print(a)显示a=[100,2,3],此即可变类型;mutable类型不能当哈希表的keymp[tuple(counts)].append(st)return list(mp.values())
5. 最长连续序列

- 利用哈希表,根据数是否是开头来判断是否跳过内层循环
利用哈希表对每个数判断是否是连续序列开头的数,如果该数的前一个在序列中,说明肯定不是开头,直接跳过;因此,只要对每个开头的数进行循环,直到这个序列不再连续
即每个数进行内层进行一次循环,外层为O(n),故时间复杂度为O(n)
class Solution:def longestConsecutive(self, nums: List[int]) -> int:longest_streak = 0num_set = set(nums) #对nums进行去重for num in num_set:if num - 1 not in num_set:current_num = numcurrent_streak = 1while current_num + 1 in num_set:current_num += 1current_streak += 1longest_streak = max(longest_streak,current_streak)return longest_streak
6. 利用双指针移动零

- 利用双指针
使用双指针,左指针指向当前已经处理好的序列尾部,右指针指向待处理序列的头部;右指针不断向右移动,每次右指针指向非零数,则将左右指针对应的数交换,同时左指针右移;左右指针中间全为零。
两个指针同时移动,每个位置最多被遍历两次,时间复杂度为O(n)
class Solution:def moveZeroes(self,nums:List[int]) -> None:n = len(nums)left = right = 0 while right < n:if nums[right] != 0:nums[left],nums[right] = nums[right],nums[left]#相当于左指针停滞不前,指向右指针原先指向的0,因此需要交换位置left += 1right += 1
7. 双指针:容器可以装的最多的水

- 利用双指针框出左右边界
每次以双指针为左右边界,移动更小数的那个指针,如果是左指针则右移,右指针则左移。
双指针总计最多遍历整个数组一次,时间复杂度为O(n)
class Solution:def maxArea(self,height:List[int]) -> int:l,r = 0,len(height) -1ans = 0while l < r:area = min(height[l], height[r])*(r-l)ans = max(ans,area)if height[l] <= height[r]:l+=1else:r-=1return ans
8. 二叉树的中序遍历及其延伸

- 树的中序遍历:按照访问左子树-根节点-右子树的方式遍历这棵树,在访问左子树的时候按照同样的方式遍历,直到遍历完整颗树。
- 方法一:利用递归
时间复杂度:O(n),n为二叉树节点的个数;
空间复杂度:O(n),递归利用了隐形栈
class Solution:def inorderTraversal(self, root):res = []self.inorder(root, res)return resdef inorder(self, root, res):if not root:returnself.inorder(root.left, res)res.append(root.val)self.inorder(root.right, res)
- 方法二:迭代,上述递归时隐式维护了一个栈,迭代时需要将这个栈显式模拟出来
时间复杂度为O(n),n为二叉树节点个数,每个节点会被访问一次且只会被访问一次;
空间复杂度为O(n),栈占用的空间
class Solution:def inorderTraversal(self, root):res = []stack = []while root or stack:# 1. 一直向左走,压入栈while root:stack.append(root)root = root.left# 2. 弹出栈顶元素,访问它root = stack.pop()res.append(root.val)# 3. 转向右子树root = root.rightreturn res
- 方法三:morris
比上述多做了一步:假设当前遍历到的节点为x,将x的左子树中最右边的节点的右孩子指向x,这样在左子树遍历完成后我们通过这个指向走回了x而不用通过栈;
时间复杂度:O(n),每个节点被遍历两次;
省去了栈的空间复杂度,O(1)。
class Solution:def inorderTraversal(self, root):res = []current = rootwhile current:if current.left:#有左子树# 找到当前节点左子树中的最右节点(中序前驱)predecessor = current.leftwhile predecessor.right and predecessor.right != current:predecessor = predecessor.right# 第一次访问:建立线索if not predecessor.right:predecessor.right = currentcurrent = current.leftelse:# 第二次访问:恢复结构 + 访问当前节点predecessor.right = None#置空res.append(current.val)current = current.rightelse:# 没有左子树,直接访问当前节点res.append(current.val)current = current.rightreturn res
- 二叉树的层次遍历:按照从上到下、从左到右的顺序一层一层访问树的节点。是一种广度优先搜索方法,通常使用队列实现。实现逻辑为:
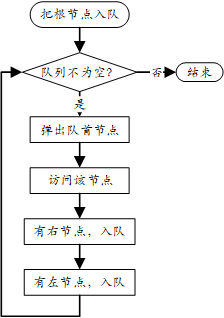
| 题型 | 说明 |
|---|---|
| 🔁 按层反转 | 每一层从右到左打印(Z字形遍历) |
| 📐 记录层数/高度 | 层数 = 阶段数,BFS循环几轮就是几层 |
| 🌠 找到每层最大值 | 每一层记录最大值 |
| 🎯 节点的最短路径 | BFS是天然找最短路径的利器 |
| 🔗 右视图/左视图节点 | 每层最右/最左节点 |
| 📦 序列化和反序列化 | 层序遍历是常用方式之一 |
- 深度优先搜索:是种“一条路走到底”的搜索方法,他优先沿某一条路走下去,走到底了再返回上一个交叉点走另一条路。
常用数据结构:递归(系统栈)或手动栈 - 广度优先搜索哦:是种“从近到远”的搜索方法,他一层一层地遍历节点,先访问第一层,再访问第二层。
常用数据结构:队列 - 无论是深度优先搜索还是广度优先搜索,其时间复杂度都是遍历的所有节点和边的成本O(n+m);但空间复杂度广度优先搜索会更高一些(排队的节点更多)。
两者区别:
| 对比项 | DFS(深度优先) | BFS(广度优先) |
|---|---|---|
| 搜索方式 | 一条路走到底,再回退 | 一层一层来,逐层扩展 |
| 使用数据结构 | 栈(或递归) | 队列 |
| 空间复杂度 | 最坏O(n)(取决于深度) | 最坏O(n)(取决于宽度) |
| 寻找路径 | 不一定是最短路径 | 一定能找最短路径(无权图) |
| 应用场景 | 回溯、树递归、组合问题、图连通 | 层级问题、最短路径、最小步数 |
| 实现方式 | 递归写法更自然 | 需要手动队列实现 |
9. 二叉树的最大深度

- 方法一:深度优先搜索
利用递归,先计算左子树深度和右子树深度,树的深度即两者最大+1;
时间复杂度:O(n),每个节点只被遍历一次
class Solution:def maxDepth(self,root):if root is None:return 0else:left_height = self.maxDepth(root.left)right_height = self.maxDepth(root.right)return max(left_height,right_height) +1
- 方法二:广度优先搜索
利用队列,将[每次从队列拿出一个节点]改为[每次将队里了里的所有节点拿出来扩展],这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,最后用一个变量来维护拓展的次数,该二叉树的最大深度即为拓展次数;
时间复杂度:O(n),每个节点只被访问一次。
class Solution:def maxDepth(self,root):if not root:returnqueue = deque([root])#加入根节点ans = 0while queue:size = len(queue)#当前层的节点数for _ in range(size):#对于该层的所有节点都进行左右节点拓展node = queue.popleft()if node.left:queue.append(node.left)if node.right:queue.append(node.right)ans += 1 #处理完一层后深度+1return ans
- 如何用python实现队列
| 方法 | 适用场景 | 入队 | 出队 | 是否推荐 |
|---|---|---|---|---|
collections.deque | 通用算法题 / BFS | append() | popleft() | ✅ 推荐 |
queue.Queue | 多线程 / 并发编程 | put() | get() | ✅ 推荐(多线程) |
list | 简单脚本 | append() | pop(0) | ❌ 不推荐(效率低,pop的时间复杂度为O(n)) 因为list底层是动态数组,删除头部元素后需要将后续前移,故时间复杂度为O(n) |
举例:
## collections.deque
from collections import dequequeue = deque()# 入队
queue.append(10)
queue.append(20)# 出队
x = queue.popleft() # 返回10# 判空
if not queue:print("队列为空")## queue.Queue
from queue import Queuequeue = Queue()# 入队
queue.put(10)# 出队
x = queue.get()# 判空
if queue.empty():print("队列为空")## list模拟
queue = []# 入队
queue.append(10)# 出队(效率低)
x = queue.pop(0)
10. 翻转二叉树

- 利用递归;交换左右子树的位置即可
时间复杂度:O(n),n为树的节点,会遍历树的每个节点,对于每个节点,在常数时间内交换两个子树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def invertTree(self,root: TreeNode) -> TreeNode:if not root:return rootleft = self.invertTree(root.left)right = self.invertTree(root.right)root.left,root.right = root.right,root.leftreturn root
11. 对称二叉树

- 方法一:递归
同步移动两个指针,两指针先同时指向根节点,接着,一个指针左移,一个指针右移,每次检查当前指针的值是否相等,如果相等再判断左右子树是否对称;
时间复杂度:O(n),对于每个节点都会遍历
class Solution:def isSymmetric(self, root: Optional[TreeNode]) -> bool:# 内部辅助函数:递归比较左右子树是否镜像对称def check(p, q):if not p and not q:return True # 两个都是空,说明对称if not p or not q:return False # 一个空一个非空,不对称return (p.val == q.val andcheck(p.left, q.right) andcheck(p.right, q.left))return check(root.left, root.right)
12.二叉树的直径

- 深度优先搜索
路径可以看成经过的节点数减一;且可以看成由某个节点为起点,其左儿子和右儿子的和(节点数为左儿子加右儿子+1,路径需要再减1);遍历所有节点得到左儿子和右儿子的和,取最大即可得到二叉树的最长路径;
时间复杂度:O(n),n为二叉树节点数,遍历所有节点;
空间复杂度:O(height),height为树的高度,递归需要为每一层递归函数分配栈空间,分配空间大小取决于递归深度,即树的高度。
class Solution:def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:self.ans = 0def depth(node):#访问到空节点,返回0if not node:return 0#左儿子为根的子树的深度L = depth(node.left)#右儿子为根的子树的深度R = depth(node.right)#计算d_node即L+R+1,并更新ansself.ans = max(self.ans,L+R)#返回该节点为根的子树深度return max(L,R)+1depth(root)return self.ans
13. 将有序数组转换为二叉搜索树

- 三个方法均是中序遍历,方法一总是选择中间位置左边的数字作为根节点,方法二选择右边,方法三在上述两者中随机选择。
时间复杂度:O(n),n为数组长度,每个是数字只访问一次;
空间复杂度:O(log(n)),构建栈的深度为log(n)。
class Solution:def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:def helper(left,right):if left > right:return None#方法一,总是选择中间位置左边的数作为根节点mid = (left+right) // 2#整数除法,向下取整#方法二,总是选择中间的右边作为根节点# mid = (left+right+1) // 2#方法三,随机选择中间节点的左边或者右边作为根节点mid = (left+right+randint(0,1)) // 2root = TreeNode(nums[mid])#确定根节点root.left = helper(left,mid - 1) #递归构建左子树root.right = helper(mid+1,right) #递归构建右子树return root return helper(0,len(nums) - 1)
- 二叉搜索树:是一种特殊的二叉树,需要满足:
对于每个节点root:
a. 所有左子树 < root.val
b. 所有右子树 > root.val
c. 所有子树均是二叉搜索树
常见操作:最坏时间复杂度是因为可能因为不断插入递增或递减序列使二叉树弱化为链表
| 操作 | 描述 | 平均时间复杂度 | 最坏时间复杂度 |
|---|---|---|---|
| 插入(Insert) | 插入一个新值 | O(log n) | O(n) |
| 查找(Search) | 查找一个值是否存在 | O(log n) | O(n) |
| 删除(Delete) | 删除一个值(需要分情况处理) | O(log n) | O(n) |
| 最小值/最大值 | 找最小值:最左节点;最大值:最右节点 | O(log n) | O(n) |
遍历方式:
| 遍历方式 | 顺序 | 应用场景 |
|---|---|---|
| 中序遍历 | 左 → 根 → 右 | 升序输出 BST 中所有值 |
| 前序遍历 | 根 → 左 → 右 | 用于复制树结构 |
| 后序遍历 | 左 → 右 → 根 | 用于删除树结构 |
| 层序遍历 | 一层一层从上往下 | 常用于广度优先搜索(BFS) |
删除操作(三种情况):
a. 叶子节点:直接删除
b. 只有一个子节点:用子节点替代它
c. 该节点有两个子节点:找右子树的最小值(或左子树最大值);用其替换当前节点,再递归删除该值
class TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightclass Solution:def deleteNode(self, root, key):if not root:return None#找到值对应的节点,小于往左,大于往右if key < root.val:root.left = self.deleteNode(root.left, key)elif key > root.val:root.right = self.deleteNode(root.right, key)else:# 找到目标节点,开始删除#单个节点,直接替换if not root.left:return root.rightif not root.right:return root.left# 两个子节点:找右子树最小值min_larger_node = self.getMin(root.right)root.val = min_larger_node.valroot.right = self.deleteNode(root.right, min_larger_node.val)#再在右子树中删除这个最小值return rootdef getMin(self, node):while node.left:node = node.left#由于是对右子树找最小,右子树的最左节点就是最小值return node
时间复杂度:查找要删除的节点/找右子树的最小值/递归删除该最小节点;三个步骤都是最多耗时O(h),h为树的高度;当树为平衡二叉树时, h = l o g ( n ) h=log(n) h=log(n),退化为链表时 h = n h=n h=n。
| 情况 | 时间复杂度 |
|---|---|
| 平衡二叉搜索树(理想情况) | O(log n) |
| 退化为链表(最坏情况) | O(n) |
相关扩展结构:
| 数据结构 | 特点 |
|---|---|
| AVL树 | 平衡二叉搜索树,插入/删除时自动保持左右子树高度差不超过1 |
| 红黑树 | 一种自平衡二叉搜索树,插入和删除更高效,广泛用于 STL、Java |
| Treap / Splay Tree | 更复杂的平衡机制,适合频繁操作或对时间复杂度有更高要求 |
| Segment Tree | 区间操作优化,但不是严格意义上的 BST |
平衡二叉树:对于任意节点,其左子树和右子树的高度差小于等于1,所有子树也是平衡二叉树。
为什么需要平衡?发现右子树过高时会自动左旋,避免树退化为链表。
常见的平衡二叉树:
| 类型 | 特点 |
|---|---|
| AVL树 | 每个节点维护平衡因子,严格控制高度差不超过 1,查找快但插入稍慢(最典型的二叉树) |
| 红黑树 | 通过颜色控制近似平衡,高度最多为 2log n,Java、C++ STL 使用 |
| Splay树 | 每次访问后将该节点“旋转”到根,适合频繁访问某些节点的场景 |
| Treap | 结合 BST + 堆的性质,使用随机优先级构建 |
操作时间复杂度:
| 操作 | 时间复杂度 |
|---|---|
| 查找 | O(log n) |
| 插入 | O(log n) |
| 删除 | O(log n) |
14. 树的层序遍历

- 方法一:利用广度优先遍历每个节点,每层均判断层中节点数。
时间复杂度:O(n),每个节点均被访问一次;
空间复杂度:O(n),队列+输出。
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:res = []if not root:return res queue = deque([root])while queue:size = len(queue)#当前层队列中节点数level = []for _ in range(size):node = queue.popleft()level.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)res.append(level)return res
- 方法二:利用哈希表
时间复杂度:O(n+hlog(h)),每个节点访问一次,最后需要对哈希表键值排序输出,时间复杂度为hlog(h),h为树的高度
空间复杂度:O(n),队列+哈希表+输出
class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []level_map = defaultdict(list) # 哈希表:level -> list of node valuesqueue = deque()queue.append((root, 0)) # 初始状态为根节点和其层级 0while queue:node, level = queue.popleft()level_map[level].append(node.val)#通过二元组加入哈希表if node.left:queue.append((node.left, level + 1))if node.right:queue.append((node.right, level + 1))# 将 level_map 按 level 从小到大取值组成结果return [level_map[i] for i in sorted(level_map.keys())]
15. 判断树是否是二叉搜索树

- 方法一:利用递归,判断该节点是否在上下界里,其左右子树是否是二叉搜索树即可。
时间复杂度:O(n),每个节点均被访问一次;
空间复杂度:O(n),构建栈的深度为树的高度,最坏情况为n。
class Solution:def isValidBST(self, root: Optional[TreeNode]) -> bool:def helper(node,lower = float('-inf'),upper=float('inf')) -> bool:if not node:return Trueval = node.val#判断节点值是否满足if val <= lower or val >= upper:return False #递归判断左右子树是否是二叉搜索树if not helper(node.right,val,upper):return Falseif not helper(node.left,lower,val):return Falsereturn Truereturn helper(root)
- 方法二:中序遍历时实时检查当前节点值是否大于前一个中序遍历得到的节点值,一旦发生不大于,则该树并非二叉搜索树;利用栈实现中序遍历。
时间复杂度:O(n),每个节点最多被访问一次;
空间复杂度:O(n),栈最多存储n个节点,因此额外需要O(n)的空间。
class Solution:def isValidBST(self,root:TreeNode) -> bool:stack,inorder = [],float('-inf')while stack or root:#把左子树节点全部压入栈中while root:stack.append(root)root = root.leftroot = stack.pop()#如果中序遍历得到的节点的值小于前一个inorder,说明不是二叉搜索树if root.val <= inorder:return Falseinorder = root.valroot = root.rightreturn True
16. 找到二叉搜索树中第k小的元素

- 方法一:利用中序遍历,边遍历边计数,计到第k个即第k小的数。
时间复杂度:O(h+k),h是树的高度,开始遍历前,需要到达最左的叶子节点;
空间复杂度:O(h),栈中最多需要存储h个元素。
class Solution:def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:stack=[]#res = [],可以省去该记录,直接用k计数即可while stack or root:while root:stack.append(root)root = root.leftroot = stack.pop()# res.append(root.val)# if len(res) == k:# return res[k-1]k-=1if k == 0:return root.valroot = root.right
- 方法二:用于优化需要频繁查找第k小的值;利用树重建,同时记录子树的节点数;对每个节点判断其左子树节点数和k的大小。
时间复杂度:O(n),需要遍历树中所有的节点来统计节点数,搜索的时间复杂度为O(H),H为树的高度;
空间复杂度:O(n),用于存储以每个节点为根节点的子树节点数。
class MyBst:def __init__(self,root: TreeNode):self.root = root#统计以每个节点为根节点的子树的节点树,并记录在哈希表中self._node_num = {}#用于存储每个节点的子树节点数self._count_node_num(root)def kth_smallest(self,k: int) -> int:#返回树中第k小的元素node = self.rootwhile node:left = self._get_node_num(node.left)#得到左子树的节点数if left < k - 1:#左子树总节点数小于knode = node.right#节点右移k -= left+ 1elif left == k - 1:return node.valelse:node = node.left#第k小的节点在左子树中def _count_node_num(self,node) -> int:#统计以node为节点的子树节点数if not node:return 0self._node_num[node] = 1 + self._count_node_num(node.left) + self._count_node_num(node.right)return self._node_num[node]def _get_node_num(self,node) -> int:#获取以node为根节点的子树节点数return self._node_num[node] if node is not None else 0class Solution:def kthSmallest(self,root: TreeNode,k: int) -> int:bst = MyBst(root)return bst.kth_smallest(k)
- 方法三:如果二叉树经常被修改(插入/删除操作)并且你需要频繁地查找第k小的值,可以将二叉搜索树变平衡。构建好平衡二叉搜索树后修改成本降低。
时间复杂度:O(n),构建树全部节点的时间,增、删、搜索的时间复杂度均为O(log(n));
空间复杂度:O(n),用于存储平衡二叉树。
class AVL:#定义一个平衡二叉树,允许重复值#定义平衡二叉树的节点class Node:__slots__ = ("val","parent","left","right","height","size")def __init__(self,val,parent = None,left=None,right = None):self.val = valself.parent = parentself.left = leftself.right = rightself.height = 0#默认叶子节点高度为0self.size = 1#当前节点为根节点时子树节点数#构建二叉树def __init__(self,vals):self.root = self._build(vals,0,len(vals) - 1,None) if vals else Nonedef _build(self,vals,l,r,parent):#根据vals[l:r]构建平衡二叉树,并返回根节点m = (l+r) // 2node = self.Node(vals[m],parent=parent)if l <= m -1:#递归构建左子树node.left = self._build(vals,l,m - 1,parent=node)if m+1 <= r:node.right = self._build(vals,m+1,r,parent=node)self._recompute(node)#重新计算每个子树的高度和元素数return nodedef _recompute(self,node):#重新计算每个子树的高度和元素数node.height = 1+ max(self._get_height(node.left),self._get_height(node.right))node.size = 1+ self._get_size(node.left) + self._get_size(node.right)def _get_height(self,node) -> int:return node.height if node is not None else 0def _get_size(sellf,node) -> int:return node.size if node is not None else 0def kth_smallest(self,k: int):node = self.rootwhile node:left = self._get_size(node.left)if left < k -1:node = node.rightk -= left+1elif left == k - 1:return node.valelse:node = node.left #对二叉树进行增删改除操作#插入值为v的节点def insert(self,v):if self.root is None:self.root = self.Node(v)else:#计算新节点的位置#在子树中找到值为v的位置node = self._subtree_search(self.root,v)is_add_left = (v<= node.val)#判断是否加在节点左边if node.val == v:if node.left:#如果值为v的节点存在且其有左子节点,则将其加在左子树的最右边node = self._subtree_last(node.left)is_add_left = Falseelse:is_add_left = True#添加新节点leaf = self.Node(v,parent=node)if is_add_left:node.left = leafelse:node.right = leafself._rebalance(leaf)#使树重新平衡def _rebalance(self,node):#从node节点开始逐个向上重新平衡二叉树,并更新高度和元素数while node is not None:old_height,old_size=node.height,node.size if not self._is_balanced(node):#判断此时是否平衡node = self._restructure(self._tall_grandchild(node))self._recompute(node.left)self._recompute(node.right)self._recompute(node)if node.height == old_height and node.size == old_size:#如果节点高度和元素数都没有变化则不需要再继续向上调整node = None else:node = node.parent def _is_balanced(self,node):#判断是否平衡return abs(self._get_height(node.left) - self._get_height(node.right)) <= 1def _tall_child(self,node):#获取node节点更高的子树if self._get_height(node.left) > self._get_height(node.right):return node.leftelse:return node.rightdef _tall_grandchild(self,node):#获取节点更高的子树里节点更高的子树child = self._tall_child(node)return self._tall_child(child)def _restructure(self,node):#重建parent = node.parentgrandparent = parent.parent if (node == parent.right) == (parent == grandparent.right):#处理一次需要旋转的情况self._rotate(parent)return parentelse:#处理需要两次旋转的情况self._rotate(node)self._rotate(node)return node def _rotate(self,node):#旋转parent = node.parentgrandparent = parent.parentif grandparent is None:self.root = node node.parent = Noneelse:self._relink(grandparent, node, parent == grandparent.left)#如果父节点在祖父节点的左边,则将node连接到祖父的左边,否则,连接到祖父的右边if node == parent.left:self._relink(parent,node.right,True)#如果节点在父节点的左边,则将节点的右子节点连接到父节点左边self._relink(node,parent,False)#将父节点连接到节点右边else:self._relink(parent,node.left,False)#节点在父节点右边,则将节点的左子节点连接到父节点右边self._relink(node,parent,True)#将父节点连接到节点的左边#is_left为真则将child连接到parent的左边,否则,连到parent的右边@staticmethoddef _relink(parent,child,is_left):#重新链接父节点和子节点,子节点允许为空if is_left:parent.left = childelse:parent.right = childif child is not None:child.parent = parent#删除操作def delete(self,v) -> bool:if self.root is None:return False node = self._subtree_search(self.root,v)#找到值为v的节点if node.val != v:#没有找到需要删除的节点return False #处理当前节点既有左子树也有右子树的情况#若左子树比右子树高度低,则将当前节点替换为右子树最左侧的节点,并移除右子树最左侧的节点#若右子树比左子树高度低,则将当前节点替换为左子树最右侧的节点,并移除左子树最右侧的节点if node.left and node.right:if node.left.height <= node.right.height:replacement= self._subtree_first(node.right)#找到右子树最左else:replacement = self._subtree_last(node.left)#找到左子树最右node.val = replacement.valnode = replacementparent = node.parentself._delete(node)self._rebalance(parent)return Truedef _delete(self,node):#删除节点并用它的子节点代替他,该节点最多只能有一个子节点if node.left and node.right:raise ValueError('node has two children')child = node.left if node.left else node.rightif child is not None:child.parent = node.parent if node is self.root:self.root = childelse:parent = node.parentif node is parent.left:parent.left = childelse:parent.right = child node.parent = node def _subtree_first(self,node):#返回以node为根节点的子树的第一个元素while node.left is not None:node = node.left return node def _subtree_last(self,node):#返回以node为根节点的子树的最后一个元素while node.right is not None:node = node.rightreturn nodedef _subtree_search(self,node,v):#在以node为根节点的子树中搜索值为v的节点,如果没有,则返回值为v的节点应该在的位置的父节点if node.val < v and node.right is not None:return self._subtree_search(node.right,v)if node.val > v and node.left is not None:return self._subtree_search(node.left,v)else:return nodeclass Solution:def kthSmallest(self,root: TreeNode,k: int) -> int:def inorder(node):if node.left:inorder(node.left)inorder_lst.append(node.val)if node.right:inorder(node.right)#中序遍历生成数值列表inorder_lst = []inorder(root)#构造平衡二叉搜索树avl = AVL(inorder_lst)#模拟1000次插入和删除操作random_nums = [random.randint(0,10001) for _ in range(1000)]for num in random_nums:avl.insert(num)random.shuffle(random_nums) #列表乱序for num in random_nums:avl.delete(num)return avl.kth_smallest(k)
17. 二叉树展开为链表

- 方法一:二叉树展开为链表之后会破坏二叉树的结构,因此在前序遍历(深度优先搜索:递归/迭代)结束之后更新各个节点的左右子节点的信息。
时间复杂度:O(n),其中,n为二叉树的节点数,前序遍历的时间复杂度为O(n),更新各个节点信息也是O(n);
空间复杂度:O(n),栈内元素不会超过n个
class Solution:def flatten(self,root: TreeNode) -> None:preorderList = list()def preorderTraversal(root:TreeNode):if root:preorderList.append(root)preorderTraversal(root.left)preorderTraversal(root.right)preorderTraversal(root)size = len(preorderList)for i in range(1,size):prev,curr = preorderList[i-1],preorderList[i]prev.left = Noneprev.right = curr#通过迭代实现前序遍历
class Solution:def flatten(self,root: TreeNode) -> None:preorderList = list()stack = list()node = rootwhile node or stack:while node:preorderList.append(node)stack.append(node)#先把左子节点全部放进来node = node.leftnode = stack.pop()#从低部开始node = node.right#重拾右子节点,并排查右子节点的左子树 size = len(preorderList)for i in range(1,size):prev,curr = preorderList[i-1],preorderList[i]prev.left = Noneprev.right = curr
- 方法二: 前序遍历和展开同步进行,在遍历左子树之前获得左右子节点的信息并存入栈中;对迭代遍历进行修改,每次从栈内弹出一个节点作为当前访问的节点,获得该节点的子节点,如果子节点不为空,则依次将右子节点和左子节点压入栈内。
时间复杂度:O(n),每个节点均被访问一次;
空间复杂度:O(n),栈的空间。
class Solution:def flatten(self,root: Optional[TreeNode]) -> None:if not root:returnstack = [root]prev = Nonewhile stack:curr = stack.pop()if prev:prev.left = Noneprev.right = currleft,right = curr.left,curr.rightif right:stack.append(right)if left:stack.append(left)prev = curr
- 方法三:寻找前驱节点,将空间复杂度降为O(1);即对于当前节点,如果左子节点不为空,则将其右子节点赋给左子节点的最右子节点作右子节点;然后将当前节点的左子节点赋给当前节点的右子节点。
时间复杂度:O(n),每个节点均被访问一次;
空间复杂度:O(1),不需要栈,直接在树中改。
class Solution:def flatten(self,root: TreeNode) -> None:curr = rootwhile curr:if curr.left:predecessor = nxt = curr.leftwhile predecessor.right:precedessor = predecessor.rightprecedessor.right = curr.rightcurr.left = Nonecurr.right = nxtcurr = curr.right
