2025五一杯B题五一杯数学建模思路代码文章教学: 矿山数据处理问题
完整内容请看文章最下面的推广群
问题1. 根据附件1中的数据和,建立数学模型,对数据A进行某种变换,使得变换后的结果与数据尽可能接近。计算变换后的结果与数据的误差,并分析误差的来源(如数据噪声、模型偏差等)对结果的影响。

问题1:数据变换模型
考虑数据A和数据B之间的映射关系,其形式从线性映射到复杂非线性变换不等。我们首先从最简约的线性变换开始,逐步引入更高阶非线性建模与小波域稀疏表示。
基础模型一:线性变换
构造模型: 其中, 为待估系数,为残差误差项。
最小二乘估计方法:
基础模型二:多项式变换
采用AIC准则选取最优阶数 。
高级模型:小波变换 + 稀疏非线性映射
步骤1:小波域处理: 提取主尺度小波系数(如Haar小波),在稀疏域降低维度。
步骤2:稀疏映射模型(Bayesian LASSO): 其中 是稀疏参数,通过贝叶斯正则化求解。
步骤3:反变换:
误差评估指标
●均方根误差(RMSE):
●**结构相似性指数(SSIM)用于评估结构保真;
●互信息(MI)**评估信息保持程度。
误差来源分析
误差来源 分析方法
测量噪声 方差估计、信噪比分析
模型偏差 Q-Q图、残差分布检测
小波系数量化误差 熵增分析,保留位数对误差影响分析
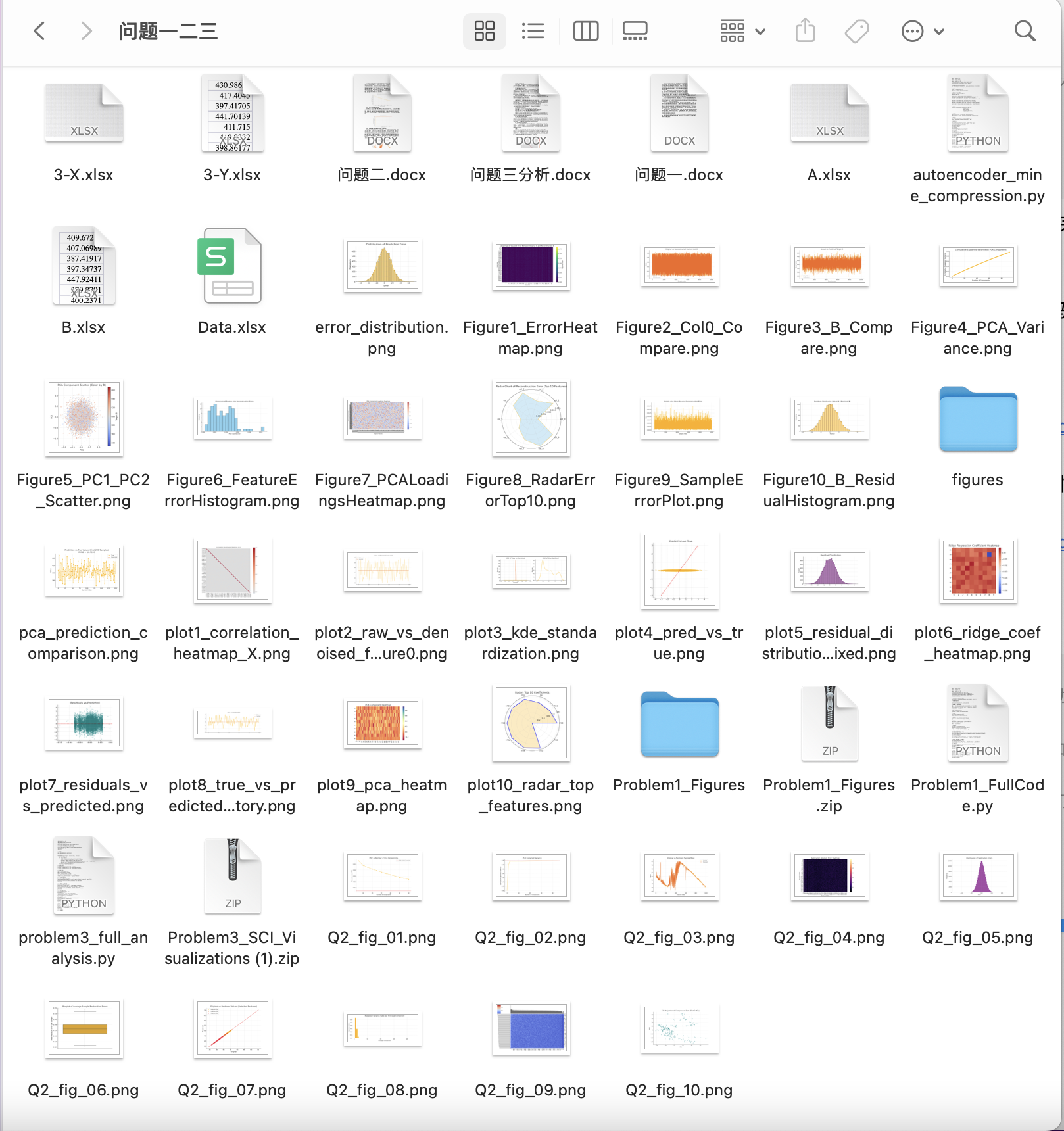
多尺度误差 多分辨率小波谱分解后逐尺度重构误差
问题2. 请分析附件2中给出的一组矿山监测数据,建立数据压缩模型,对附件2中的数据进行降维处理,计算压缩效率(包括但不限于压缩比、存储空间节省率等)。进一步建立数据还原模型,将降维后的数据进行还原,分析降维和还原对数据质量的影响,提供还原数据的准确度(MSE不高于0.005)和误差分析。(要求在保证还原数据的准确度的前提下,尽可能地提高压缩效率)

问题2:矿山监测数据压缩与还原
在保证重构MSE小于0.005的前提下,尽可能提高压缩效率。
基础模型:PCA与SVD
对于附件2中的矿山监测数据,首先考虑经典的降维方法:
●PCA变换:
取前个主成分投影:
●SVD压缩:
压缩后数据表示为
高级模型:深度自编码器与张量分解
●VAE结构:
●Tucker张量分解: 通过约束核张量 的维度实现压缩。
压缩评估指标
●压缩比:
●空间节省率:
●MSE:
多层还原机制
●小波软阈值反压缩
●残差网络学习误差
●实时误差反馈调节压缩率
为确保还原MSE不高于0.005,设计多层级还原策略:
●自适应小波阈值去噪:
●- 对压缩数据应用小波变换
●- 使用自适应软阈值消除压缩噪声
●- 反变换获得平滑还原数据
●残差网络优化:
●- 构建残差网络学习还原误差:R(X̂) ≈ X - X̂
●- 最终还原结果:X_restored = X̂ + R(X̂)
●误差控制反馈机制:
●- 实时监控还原MSE
●- 当MSE超过阈值时,减小压缩比
●- 动态调整压缩参数确保MSE < 0.005
问题3. 在矿山监测数据分析过程中,往往需要处理各类噪声的影响。请分析附件3中给出的两组矿山监测数据,对数据X进行去噪和标准化处理,建立X与Y之间关系的数学模型,计算模型的拟合优度,进行统计检验,确保模型具有较强的解释能力。(要求给出清晰的数据预处理方法说明、建模过程、拟合优度计算过程及误差分析)

问题3:噪声处理与关系建模
预处理方法
●中值滤波处理极端异常值
●小波去噪(使用Daubechies-4)
●Z-score标准化:
基础模型:多元回归
高级模型:高斯过程回归(GPR)+ 模态分解
●核函数形式:
●混合模型(Stacking)集成SVR、RF、XGBoost。
统计检验与误差分析
●R²、Adjusted R²;
●F检验整体显著性,t检验变量显著性;
●Durbin-Watson测试自相关性;
●残差正态性检验(Shapiro-Wilk)。
问题4. 请分析附件4给出的两组矿山监测数据,建立X与Y之间关系的数学模型,设计使得数学模型拟合优度尽可能高的参数自适应调整算法,并给出自适应参数与数学模型拟合优度的相关性分析,计算模型的平均预测误差,评估模型的稳定性和适用性。

问题4:参数自适应调整算法
基础建模流程
1.假设模型形式:
2.通过梯度下降最小化损失函数;
3.使用k折交叉验证提升鲁棒性。
高级优化算法
●贝叶斯优化:
●差分进化算法(DE):
稳定性与相关性评估
●Sobol敏感性指数;
●鲁棒性系数 ;
●参数变异系数
问题5. 对矿山监测高维数据进行降维处理,为了高效使用降维后的数据,需要建立降维数据到原始数据空间的重构模型。重构模型要求能恢复数据的主要特征,保持数据的可解释性。因此,探讨降维与重构之间的平衡关系,具有重要研究意义。请对附件5中的数据X,建立数学模型进行降维处理,并对降维后的数据进行重构,建立重构数据与附件5中Y之间关系的数学模型,评估所建立数学模型的效果(包括但不限于模型的泛化性、相关算法的复杂度分析等)。

问题5:高维数据降维与重构建模
基础模型:非线性降维与重构技术
●针对附件5中数据X的处理:
●流形学习降维:
●- t-SNE降维保持数据局部结构
●- UMAP算法平衡局部与全局结构
●- Isomap算法保持测地距离关系
●基本重构策略:
●- 反向映射:X̂ = g(Z),其中Z为降维数据
●- 最小化重构误差:min ||X-X̂||₂²
●- 保持关键特征指标
高级模型:深度生成网络与图结构保持
流形降维方法
●t-SNE保持局部结构;
●Isomap保持测地距离;
●UMAP兼顾全局与局部。
深度模型
●图正则化自编码器(GRAE): 其中 为拉普拉斯矩阵。
●GAN重构 + 预测:
●联合优化目标:
效果评估
●多折交叉验证下的泛化性指标;
●O(n³)复杂度分析;
●可解释性通过特征重要性评分。
总结与优化方向
通过对矿山监测数据的全面分析与建模,提出了一系列从基础到高级的数学模型与算法。针对数据变换、压缩与还原、关系建模和参数优化等核心任务,融合了传统统计方法与现代深度学习技术,构建了系统化解决方案。特别是在高维数据处理方面,通过张量分解、变分自编码器与图正则化等技术实现了高效降维与精确重构,为矿山数据分析提供了理论支撑与技术方法。
