专题四_前缀和_一维前缀和

一：题目

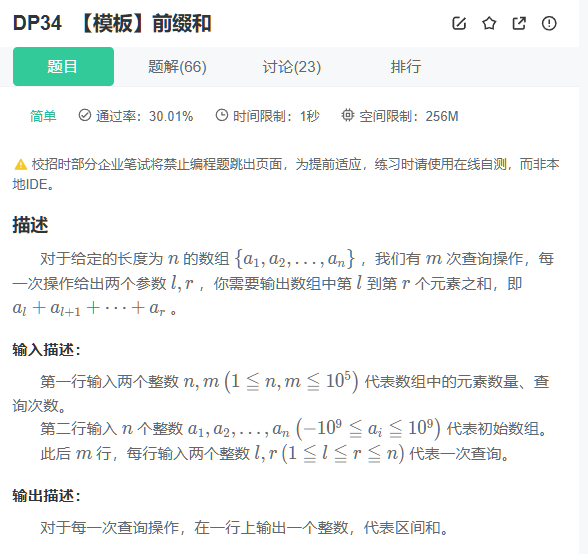
解释：给你一个数组，再给你两个值(会给m次)，这两个值是一段区间的左右边界，求区间的和

注意：

• 输入：L = 1, R = 3

• 含义：求的是原数组 arr[0] + arr[1] + arr[2] 的和。

所以很显然，题目默认L或R为1，代表数组下标为0的元素，所以为了让代码中的下标和题目描述的下标一一对应，我们后面创建数组arr来接受题目给我们的数组的时候，选择让arr数组从索引 1 开始使用。arr[1] 存储第一个数，arr[2] 存储第二个数，以此类推。索引 0 的位置我们空出来不用！这样题目L或R给几，我们就能直接当做arr的下标使用！

所以，arr数组应该比题目的数组多开辟一个位置，然后把下标0空出来

二：算法

一切的前提都是我们创建的接收题目数组的数组，假设为arr，是多一个空间，从下标1开始使用

1：暴力

暴力解法很简单，给我们LR，我们就从arr数组的下标L一直累加到下标R

而暴力的最差情况，就是询问我们m次，每次给的L和R就是整个arr数组下标1到n，也就是整个每次都让你求整个数组的大小，所以暴力时间复杂度为O(m.n)

Q：为什么你说R会为n?

A：题目认定了下标从1开始，所以题目可以给n，代表数组最后一个元素！

2：前缀和

①：前缀和求区间和的速度

前缀和算法的核心思想：用空间换时间。它通过预先计算并存储一个“前缀和数组”，使得之后计算任意区间和的操作可以在常数时间(O(1))内完成。

我们用一个具体的例子来说明：

假设题目传给我们的原始数组为：[2, 4, 1, 6, 3]

此时我们制造一个前缀和数组：dp= [0,2, 6, 7, 13, 16]

前缀和：就是dp[ i ]等于原始数组中第一个到第i个元素的和，比如dp[3] = 7，代表7等于原始数组中从第一个元素到第3个元素的和，也就是2+4+1=7！

Q1：为什么dp要多开辟一个空间，然后把下标为0位置空着，从下标为1位置开始使用？

A1：这是前缀和的固定做法，这样设计的好处有两个：

①：不用担心边界的处理，这点在后面会谈到

②：这样设计dp[ i ]才能代表原始数组中第一个元素到第i个元素的和！也就是前i个元素的和

图示如下：

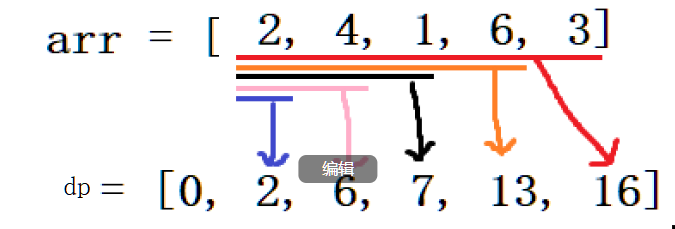
注：dp[i]中的i是pd数组的下标，而arr从第一个到第i个的i，是元素的数量，所以不要混淆

Q2：那这样请问对题目有什么帮助？

A2：题目问得就是第L个元素到第R个元素的和，而我们有了fd数组，我们只需要dp[R]-dp[L-1]，就能求到题目问的第L个元素到第R个元素的和！

比如现在题目问我们L是2，R为4，也就是第二个元素到第四个元素这段区间的和，则我们只需要fd[R]-fd[L-1]，也就是fd[4]-fd[1]就是答案！

因为这相当于你在一段大区间（arr的2,4,1,6）里面求一段小区间的和（arr的4,1,6），则你只需使用大区间（arr的2,4,1,6）减去另外一段小区间（arr的2）的和即可，所以这也是为什么dp[R]-dp[L-1]中的L需要-1的原因，因为另外段小区间（arr的2）的和，就是dp数组中L下标的前一个小标对应的元素，也就是dp[L-1]！

图解如下：

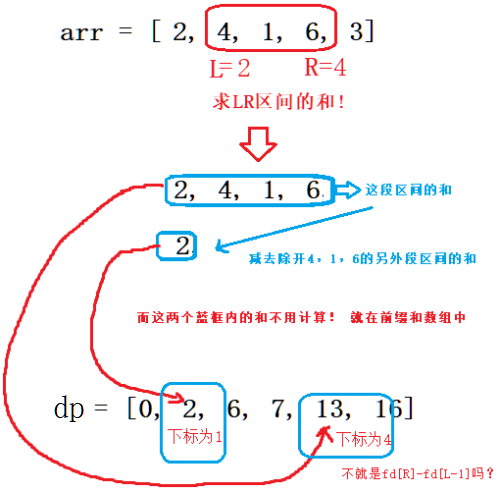
所以，不管题目的LR是多少，我们只需返回dp[R]-fd[L-1]的值即可！时间复杂度为O(1)，而查询了m次，所以总的时间复杂度为O(m)，而创建前缀和数组的空间复杂度为O(n)

时间复杂度：O(m)

空间复杂度：O(n)

所以远比O(m.n)优秀得太太太太多~~，这就是空间换时间！

②：前缀和数组怎么创建

所以，现在的问题在于怎么创建前缀和，很显然，要求dp[ i ]的值，我们不能每次都是从arr数组中的第一个累加到第i个，如果arr数组很长，则我们创建前缀和数组的时间复杂度为O(n^2)，超时！

a：原始数组从下标0开始使用

而dp[i] 的定义是：存储原数组 arr 中前 i 个元素的和。

并且，我们的dp的第一个元素是不用的，dp数组从1下标开始使用，此时arr和dp数组对应关系如下

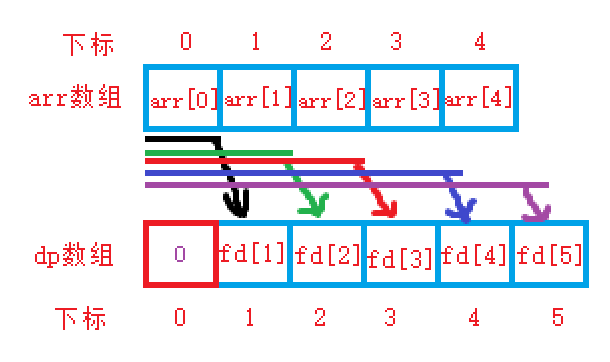
此时的公式为：dp[i] = dp[i-1] + arr[i-1]，其中dp[i]说白了就是比dp[i-1]要多加上一个arr里面的数，这个数就是arr[i-1]！

这样的确符合fd[i] 的定义是：存储原数组 arr 中前 i 个元素的和。

但是不太好记，不太优雅，如果是dp[i] = dp[i-1] + arr[i]的话，那就太好了，这就很好记， 求dp[i]就是dp[i-1]+arr[i]即可，我们dp[i]中的i是几，则dp[i-1]+arr[几]就行!并且这也是前缀和的标准公式，那怎么才能达到这个公式呢？？

b：原始数组从下标1开始使用

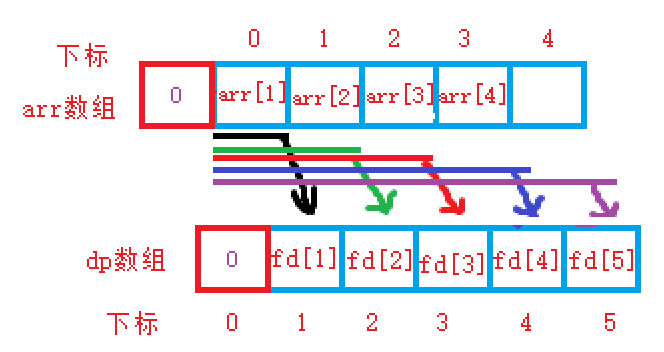
也就是我们使用arr数组接收题目给我们的原始数组的时候，我们让arr和dp数组一样，也是多开一个空间，然后从下标1开始使用！

现在的公式就变成了：dp[i] = dp[i-1] + arr[i]

Q：你把原始数组arr强行的多开辟一个，此时不是dp[i]就不能代表原始数组arr的前i个元素的了吗？因为arr在0位置多了一个元素啊？

A：arr是用来接收题目给我们的原生数组的，arr不是原生数组，所以arr是否多开辟一个空间，和dp[i]代表原始数组的前i个元素之间，不会互相影响，而arr多开辟一个空间，玩完全是为了我们创建前缀和数组时候的公式好看一点！

最后我想说，其实这两种写法，都是一样的效果，都不会进行边界的判断，为什么？因为不管是dp[i] = dp[i-1] + arr[i-1] 还是 dp[i] = dp[i-1] + arr[i] ，这两个公式的i最小都是固定为1的，因为我们的dp数组的下标就是从1开始使用的！所以[ ]里面的下标最小也是0，不会越距！

三：题目的L和R

我们谈了arr和dp数组都应该多开辟一个空间，从下标为1处开始使用，这意味这，

创建前缀和数组的公式为：dp[i] = dp[i-1] + arr[i]

求LR区间的和的公式为：dp[R]-dp[L-1]

现在还剩最后一个问题！

Q：题目规定L或R为1的时候，代表数组的第一个元素，如果L或R是0代表数组的第一个元素呢？题目的输入约定，会对我们现有的思路造成影响吗？

A：会！

题目约定1还是0代表第一个元素；

约定1，也就是题目想直接用L和R表示第几个罢了；

约定0，则代表题目想用L和R表示下标罢了；

例子：比如 L = 1， R = 3；

约定1：数组的第1个元素到第三个元素的和为多少？

约定0：数组从下标为1到下标为3的元素的和为多少？

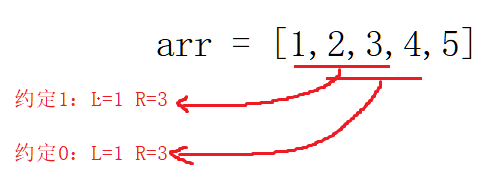
所以答案是不一样的！后者约定0求得区间是相较于约定1的区间，向后错位1个位置，也就是我们的求和公式dp[R]-dp[L-1]不对了，那怎么办？很简单，既然你约定0，求的区间整体向后移动1个位置，那我们的公式仍然为dp[R]-dp[L-1]！不过，L和R需要在使用公式正确双双+1！

所以不管题目约定的是什么，我们心里要清楚，dp[i]代表的是题目给的数组的前i个数的和即可！所以我们只需要把L和R转换为L指的是第几个数，R指的是第几个数，而约定1，L和R就是代表的第几个数，而约定0，则L和R需要双双+1，然后再使用dp[R]-dp[L-1]

四：总结前缀和算法

1：创建前缀和数组

前缀和数组bp一定要从下标1开始使用，其次接收原生数组的arr数组也要从下标1开始使用，

这样的好处在于：

①：dp[i]代表原生数组的前i个元素的和

②：创建前缀和数组公式为：dp[i] = dp[i-1] + arr[i]

不推荐！：而你若是想让arr从0开始，也就是直接接收原生数组，也可以，不过创建前缀和数组的公式为：dp[i] = dp[i - 1] + arr[i-1]

2：使用前缀和数组

求区间的和的公式恒定为：dp[R]-dp[L-1]

而题目约定1为原生数组的初始元素，则直接使用dp[R]-dp[L-1]

若题目约定0为原生数组的初始元素，则先让L和R双双++，然后再使用dp[R]-dp[L-1]；

不推荐！：你也可以在使用公式的时候再++，也就是 dp[R+1] - dp[L]

五：代码

1：arr从下标为1处开始

#include <iostream>
#include<vector>
using namespace std;//创建的arr 和 dp 都从下标1开始使用
int main() {int n ;//接收数组的元素个数int q ;//接收查询次数cin >> n >> q;vector<int> arr(n + 1); //创建arr数组来接受传进来的数组 从arr数组的下标1处开始接收for (int i = 1; i < n + 1; i++) {cin >> arr[i];}vector<long long> dp(n + 1);//预处理dp数组 dp数组从1开始存储元素for (int i = 1; i <= n; i++) {dp[i] = dp[i - 1] + arr[i];}int l, r;//查询区间的左右边界while (q--) {//进行q次查询 没cin >> l >> r;cout << dp[r] - dp[l - 1] << endl ;}}

2：arr从下标为0处开始

#include <iostream>
#include<vector>
using namespace std;//创建的arr 和 dp 都从下标1开始使用
int main() {int n ;//接收数组的元素个数int q ;//接收查询次数cin >> n >> q;vector<int> arr(n ); //创建arr数组来接受传进来的数组 从arr数组的下标0处开始接收for (int i = 0; i < n ; i++) {cin >> arr[i];}vector<long long> dp(n + 1);//预处理dp数组 dp数组从1开始存储元素for (int i = 1; i <= n; i++) {dp[i] = dp[i - 1] + arr[i-1];//公式变了}int l, r;//查询区间的左右边界while (q--) {//进行q次查询 没cin >> l >> r;cout << dp[r] - dp[l - 1] << endl ;}}

六：不推荐的写法

那这时候，就有人要问了，我就偏偏让arr和dp数组都从下标为0处开始使用，能不能写出代码通过呢？这种情况博主当然想到了，当然是可以的！不过这种写法，纯粹是胡~~~~~~闹！

首先不仅违背了bp[i]代表原生数组的前i个数的和意义，其次还多了两次的边界处理！所以你可以选择arr从0开始，但是千万不要选择前缀和数组dp从0开始！

#include <iostream>
#include<vector>
using namespace std;//创建的arr 和 dp 都从下标0开始使用
int main() {int n ;//接收数组的元素个数int q ;//接收查询次数cin >> n >> q;vector<int> arr(n);//创建arr数组从0下标来接受传进来的数组for (int i = 0; i < n; i++) {cin >> arr[i];}vector<long long> dp(n);//预处理dp数组，从0下标开始使用for (int i = 0; i < n; i++) {if (i == 0 ) dp[i] = arr[i];//对i为0 造成dp[i - 1]--->dp[-1]的处理elsedp[i] = dp[i - 1] + arr[i];}int l, r;//查询区间的左右边界while (q--) {//进行q次查询 没cin >> l >> r;if (l == 1)//对l-1--> dp[-1]越界的处理cout << dp[r - 1] - 0 << endl ;elsecout << dp[r - 1] - dp[l - 2] << endl ;}
}
//dp[i]：代表在arr数组中，i-1及其i-1左侧所有元素和

解释：可能这样唯一有意思的地方在于，我们的dp和arr数组又对齐了，因为两个数组都是从0开始使用，所以求bp[i]的公式，用的是 dp[i] = dp[i - 1] + arr[i]; 哈哈哈哈哈哈哈!!