【算法笔记 day six】二分算法的第三部分

这篇文章是二分答案的第二部分题目，这块题不少，分两次写。所有代码均为手搓或者优秀题解，大家可以放心使用，虽然不是最优解QAQ

算法笔记系列是作者在算法学习过程中的学习记录，会记录一些题目和通用方法，这块系列的更新不会暂停（因为力扣题是刷不完的哈哈哈），反正三四年内肯定是会持续更。我是一天一道，所以更新速度不会太快，喜欢的朋友可以follow，防止迷路。

闲话少叙，我们进入正题~
 

1、二分间接值

这种题目其实就是：二分的不是答案，而是一个和答案有关的值（间接值），我们通过二分求这个值的同时，不仅要记录答案，还要写好can判断函数。

例题1 — 3143.正方形中的最多点数

给你一个二维数组 points 和一个字符串 s ，其中 points[i] 表示第 i 个点的坐标，s[i] 表示第 i 个点的 标签 。

如果一个正方形的中心在 (0, 0) ，所有边都平行于坐标轴，且正方形内 不 存在标签相同的两个点，那么我们称这个正方形是 合法 的。

请你返回 合法 正方形中可以包含的 最多 点数。

注意：

• 如果一个点位于正方形的边上或者在边以内，则认为该点位于正方形内。
• 正方形的边长可以为零。

示例 1：

输入：points = [[2,2],[-1,-2],[-4,4],[-3,1],[3,-3]], s = "abdca"

输出：2

解释：

边长为 4 的正方形包含两个点 points[0] 和 points[1] 。

示例 2：

输入：points = [[1,1],[-2,-2],[-2,2]], s = "abb"

输出：1

解释：

边长为 2 的正方形包含 1 个点 points[0] 。

示例 3：

输入：points = [[1,1],[-1,-1],[2,-2]], s = "ccd"

输出：0

解释：

任何正方形都无法只包含 points[0] 和 points[1] 中的一个点，所以合法正方形中都不包含任何点。

提示：

• 1 <= s.length, points.length <= 105
• points[i].length == 2
• -109 <= points[i][0], points[i][1] <= 109
• s.length == points.length
• points 中的点坐标互不相同。
• s 只包含小写英文字母。

基础版

class Solution:def maxPointsInsideSquare(self, points: List[List[int]], s: str) -> int:left, right = 0, 1000000000def can(mid):dicts = defaultdict(int)  # 在函数内部定义，每次调用时自动清零for i, (x, y) in enumerate(points):# 使用绝对值判断点是否在正方形内if abs(x) <= mid and abs(y) <= mid:if dicts[s[i]] > 0:  # 如果该字符已经出现过return Falseelse:dicts[s[i]] += 1return Trueresult = 0while left <= right:mid = (left + right) >> 1if can(mid):result = sum(1 for i, (x, y) in enumerate(points) if abs(x) <= mid and abs(y) <= mid)left = mid + 1else:right = mid - 1return result

简洁版

class Solution:def maxPointsInsideSquare(self, points: List[List[int]], s: str) -> int:ans = 0def check(size: int) -> bool:vis = set()for (x, y), c in zip(points, s):if abs(x) <= size and abs(y) <= size:  # 点在正方形中if c in vis:return Truevis.add(c)nonlocal ansans = len(vis)return False# 注意 range 并不会创建 list，它是 O(1) 的bisect_left(range(1_000_000_001), True, key=check)return ans

#思路

由于正方形边长越大，越不合法，有单调性，所以可以二分边长的一半。

在二分中统计遇到的字符，如果没有遇到重复的字符，说明正方形合法，用字符个数更新答案的最大值。

上述代码其实思路都是一样，只是下面那个更加简洁，把一些部分通过函数缩写了，然后把计数的步骤加在函数里面

细节：

1、比较的时候记得用绝对值，只要两个值都小于mid这个点就在正方形里面

2、这题初始右边界可以直接用下面提示给的最大值，二分的话值大也不会很慢，如果对每组去写函数求最大值反而时间还更慢

3、nonlocal ans 告诉 Python 解释器：“我在这里修改的 ans，不是一个新的本地变量，而是外层函数 maxPointsInsideSquare 中定义的那个 ans。”

例题2 — 1648.销售价值减少的颜色球（难）

你有一些球的库存 inventory ，里面包含着不同颜色的球。一个顾客想要 任意颜色 总数为 orders 的球。

这位顾客有一种特殊的方式衡量球的价值：每个球的价值是目前剩下的 同色球 的数目。比方说还剩下 6 个黄球，那么顾客买第一个黄球的时候该黄球的价值为 6 。这笔交易以后，只剩下 5 个黄球了，所以下一个黄球的价值为 5 （也就是球的价值随着顾客购买同色球是递减的）

给你整数数组 inventory ，其中 inventory[i] 表示第 i 种颜色球一开始的数目。同时给你整数 orders ，表示顾客总共想买的球数目。你可以按照 任意顺序 卖球。

请你返回卖了 orders 个球以后 最大 总价值之和。由于答案可能会很大，请你返回答案对 109 + 7 取余数 的结果。

示例 1：

输入：inventory = [2,5], orders = 4
输出：14
解释：卖 1 个第一种颜色的球（价值为 2 )，卖 3 个第二种颜色的球（价值为 5 + 4 + 3）。
最大总和为 2 + 5 + 4 + 3 = 14 。

示例 2：

输入：inventory = [3,5], orders = 6
输出：19
解释：卖 2 个第一种颜色的球（价值为 3 + 2），卖 4 个第二种颜色的球（价值为 5 + 4 + 3 + 2）。
最大总和为 3 + 2 + 5 + 4 + 3 + 2 = 19 。

示例 3：

输入：inventory = [2,8,4,10,6], orders = 20
输出：110

示例 4：

输入：inventory = [1000000000], orders = 1000000000
输出：21
解释：卖 1000000000 次第一种颜色的球，总价值为 500000000500000000 。 500000000500000000 对 109 + 7 取余为 21 。

提示：

• 1 <= inventory.length <= 105
• 1 <= inventory[i] <= 109
• 1 <= orders <= min(sum(inventory[i]), 109)

差值索引法

class Solution:def maxProfit(self, inventory: List[int], orders: int) -> int:su = 0arr = [0]if len(inventory) <= 1: # 考虑特殊情况，防止下面索引outreturn (2 * inventory[-1] - orders + 1) * orders // 2 % (1000000000 + 7)inventory.sort(reverse = True) # 降序排序for i in range(1, len(inventory)): # 构建差值数组arr.append(inventory[i - 1] - inventory[i])arr.append(inventory[-1]) # 再补一位，刚刚好可以用完整个inventory数组，这个不能漏for i, j in enumerate(arr[1:], 1): # i一定是要从1开始的if orders >= i * j:temp = (2 * inventory[i - 1] - j + 1) * j // 2 # 数学公式的转换su += i * temporders -= i * j # 记得乘上索引代表前面所有的球都买else: # 计算orders不够的情况a = orders % ib = orders // i temp = (2 * inventory[i - 1] - b + 1) * b // 2su += temp * i + (inventory[i- 1] - b) * a #合并除不尽的情况更简洁breakreturn su % (1000000000 + 7) #记得要取模，满足题意并且防止数值太大溢出

二分 + 贪心

class Solution:def maxProfit(self, inventory: List[int], orders: int) -> int:# 二分查找# 提示2：存在某个值k，其中所有价值大于k的球均卖出，部分（可能为0）价值为k的球卖出# 要想求出最大总价值和，应该让k尽可能小，这样在卖出一样球的情况下，k越小，所累加的价值就越高# 检查对于价值大于k的球的个数，是否超过orders，找到最小的k# 找到k之后，说明最初价值大于k的球都会卖出，卖的个数为(inventory[i]-k)，这部分球的卖出的价值可以用等差数列求和# ans += (inventory[i] + k + 1) * (inventory[i] - k) // 2 if inventory[i] > k# 剩下一部分价值为k的球（可能没有）需要卖出，才能够卖出orders，那么这部分球的个数rest = orders - sum# 这一部分球的价值和再加到最终答案中，ans += rest * kmod = 10**9+7l = 0r = max(inventory)while l <= r:mid = (l + r) >> 1# 假设价值大于mid的球全部卖出s = sum(x - mid for x in inventory if x > mid)# 如果价值大于mid的球的个数大于需要卖出的球的个数，说明这个k值应该更大才对if s > orders:l = mid + 1# 否则这个k值应该更小才对else:r = mid - 1k = lrange_sum = lambda x, y : (x + y) * (y - x + 1) // 2rest = orders - sum(x - k for x in inventory if x > k)ans = 0for x in inventory:if x > k:ans += range_sum(k+1, x)ans += rest * kreturn ans % mod

#思路

这题我其实一开始没看出二分，直接就想到去做差分数组。所以第一种方法是我写的，由于过程都是用数学公式去计算，不是那种遍历的写法，整个速度会很快并且占得空间很小，相较于第二种方法会快很多，空间的使用也很少。方法二是别人的题解，大家可以瞅瞅，我这里主要讲方法一。

由于价值要越大越好并且可以无视顺序，这个时候看过我前面文章的小伙伴应该就可以想到，我们应该用数去计算而不是用结构去计算，我们可以把需要的数从原始结构中提取出来，数学方法绝对是又快又省空间。

这里我们先对原有数组降序排序，不难想到，当第一个数字降到和第二个数字一样大的时候，我们就要停止往下减，这个时候就要同时考虑两个数，并且这两个数是要一起下减（因为前面的数减小，后面的数就大了，我们是贪心的想要更大的数）。这里我举个例子

以 inventory = [2,5], orders = 4 为例： 排序后：[5,2]  arr = [0, 3, 2]（差值数组）索引[0, 1, 2]

可以看出，其实差值数组的索引就是要考虑的数，他的值就是前面要考虑的这些数要可以一次一起降多少

那么根据上面这个例子，因为arr第一个数是0，这个是要跳过的，我的代码里面arr的索引是从1开始的，这个要注意。因为第一个数前面是没有数去下降了。我们直接看索引1的位置，索引是1代表前面有一个数要考虑，对应arr的值是3，代表他要降3次，那么我们的value要加3次，即5+4+3，不难看出，我们可以对这个过程进行数学公式推导=n*(n- 1)*(n-2)*....*(n-k)=n*k-(k-1)*k//2，再次化简就可以得到我代码中的式子，这个就是普通的降数的过程，记得写完要乘上索引，因为前面的数要降是一起的，这个过程是一样的。只要orders大于等于i*j,即arr索引乘值，就可以进入普通过程（因为要取的球够）

这个过程不用考虑前后两个数相等的情况，因为这样减出来j会直接是0，那么算出来的temp、orders加的数也一定都是0，相当于跳过没加直接到下一步。

如果要取的球不够就要进入下一个分支，前面已经说了要降肯定是要一起降的，假设我们要降三个8，相当于i=3，inventory[i-1] = 8（前面的数已经全是8了），那么这个时候其实就是两种情况，要么刚刚好三个全都降，要么只能降一部分，这个时候其实可以分开算各自的值，如果够，那么取余数就是0，只能降一部分的式子算出来就是0。

有点难理解，大家可以动动笔好好想想，这题确实不好写

2、最小化最大值

本质是二分答案求最小。二分的 mid 表示上界。

好比用一个盖子（上界）去压住最大值，看看能否压住（check 函数）。

一定要注意我们二分要求的就是最小值，最大值是在我们can函数判断的时候才体现出来的。

例题3 — 410.分割数组的最大值（困难）

给定一个非负整数数组 nums 和一个整数 k ，你需要将这个数组分成 k 个非空的连续子数组，使得这 k 个子数组各自和的最大值 最小。

返回分割后最小的和的最大值。

子数组 是数组中连续的部份。

示例 1：

输入：nums = [7,2,5,10,8], k = 2
输出：18
解释：
一共有四种方法将 nums 分割为 2 个子数组。 
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

示例 2：

输入：nums = [1,2,3,4,5], k = 2
输出：9

示例 3：

输入：nums = [1,4,4], k = 3
输出：4

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 106
• 1 <= k <= min(50, nums.length)

class Solution(object):def splitArray(self, nums, k):""":type nums: List[int]:type k: int:rtype: int"""a = sum(nums)left, right = a // k, a # 边界优化def can(mid): # 用函数判断这个值是否是最大值temp = nums[0] # 如果不从数组第一个数开始遍历的话，也可从res=1开始res = 0for i in nums[1:]:if temp + i > mid:res += 1if res > k or temp > mid: # 别忘了判断temp本身的值也没有比mid大，因为可能会出现没有加而单个数就很大的情况，那上面这个if就无法判断了return Falsetemp = i continue # 如果没有continue，那会每次都加上itemp += iif res + 1 > k : # 无论最后一个temp是大是小，都会占一个分割数组的位置return Falseelse:return Truewhile left <= right: # 闭区间模版，二分求最小值mid = (left + right) >> 1if can(mid):right = mid - 1else:left = mid + 1return left

#思路

这题也不好写，做了一个小时才搞出来。原本想着不用二分，去求每个数组里平均值的位置最近得到解，发现不太行，最后还是只能回到二分用判断函数来解。

整体思路就是，我要求一组子数组和，这些和在所有可能的分组中是要是最小的，然后要在这个最小值里面找到最大值。所以我们二分要去找最小值，而判断的时候要判断其是否是最大值。这就是整体思路。

细节
下面代码采用闭区间二分，这仅仅是二分的一种写法，使用开区间或者半闭半开区间都是可以的。

设 nums 的元素和为 S。

开区间左端点初始值：max(nums)−1。元素和不可能比数组最大值还小，一定不满足要求。
开区间右端点初始值：S。无需分割，一定满足要求。
注：也可以用平均值 S/k 优化左端点初始值，留给感兴趣的读者思考。（如果平均值小，那和必然小于总的数组和，不符合条件了）

其余细节可以看注释内容

问：如何保证二分结果一定对应着一个划分成 k 段的方案？

答：把二分结果代入 check 函数，可以得到一个划分成 ≤k 段的方案。在此基础上，可以得到划分成 k 段的方案。比如划分成 k−1 段，那么把其中的一个长度至少为 2 的段分成两段，这两段的元素和都比原来的一段小，也满足题目要求，这样就得到了一个划分成 k 段的方案。换句话说，题目其实相当于：把数组划分成至多 k 段。（如果一个mid分出来的自数组个数不够，那就继续分割除最大子数组外的子数组，直到分成k段）

问：设二分算出来的答案为 ans，如何保证至少有一个子数组的元素和恰好等于 ans？

答：用反证法证明。假设所有子数组的元素和都小于 ans，也就是小于等于 ans−1。这意味着 can(ans−1)=true，但是二分结束后必定有 can(ans−1)=false，矛盾，所以至少有一个子数组的元素和恰好等于 ans。（即ans才是你最后得到的答案（所以can（ans-1）是false），如果最大值只有ans-1的话，那can（ans-1）不能为false才对）

例题4 — 2064.分配给商店的最多商品的最小值

给你一个整数 n ，表示有 n 间零售商店。总共有 m 种产品，每种产品的数目用一个下标从 0 开始的整数数组 quantities 表示，其中 quantities[i] 表示第 i 种商品的数目。

你需要将 所有商品 分配到零售商店，并遵守这些规则：

• 一间商店 至多 只能有 一种商品 ，但一间商店拥有的商品数目可以为 任意 件。
• 分配后，每间商店都会被分配一定数目的商品（可能为 0 件）。用 x 表示所有商店中分配商品数目的最大值，你希望 x 越小越好。也就是说，你想 最小化 分配给任意商店商品数目的 最大值 。

请你返回最小的可能的 x 。

示例 1：

输入：n = 6, quantities = [11,6]
输出：3
解释： 一种最优方案为：
- 11 件种类为 0 的商品被分配到前 4 间商店，分配数目分别为：2，3，3，3 。
- 6 件种类为 1 的商品被分配到另外 2 间商店，分配数目分别为：3，3 。
分配给所有商店的最大商品数目为 max(2, 3, 3, 3, 3, 3) = 3 。

示例 2：

输入：n = 7, quantities = [15,10,10]
输出：5
解释：一种最优方案为：
- 15 件种类为 0 的商品被分配到前 3 间商店，分配数目为：5，5，5 。
- 10 件种类为 1 的商品被分配到接下来 2 间商店，数目为：5，5 。
- 10 件种类为 2 的商品被分配到最后 2 间商店，数目为：5，5 。
分配给所有商店的最大商品数目为 max(5, 5, 5, 5, 5, 5, 5) = 5 。

示例 3：

输入：n = 1, quantities = [100000]
输出：100000
解释：唯一一种最优方案为：
- 所有 100000 件商品 0 都分配到唯一的商店中。
分配给所有商店的最大商品数目为 max(100000) = 100000 。

提示：

• m == quantities.length
• 1 <= m <= n <= 105
• 1 <= quantities[i] <= 105

class Solution:def minimizedMaximum(self, n: int, quantities: List[int]) -> int:# 检查是否能使用最大商品数 x 完成分配def check(mx):t = 0for i in quantities:t += (i + mx - 1) // mx  # 计算每种商品需要的商店数return t <= nleft, right = 1, max(quantities)  # 初始化右边界为 max(quantities)while left <= right:mid = (left + right) >> 1  # 查找中值if check(mid):  # 如果 mid 可以完成分配，尝试更小的 xright = mid - 1else:  # 否则增大 xleft = mid + 1return left  # 返回最小的 x

#思路

相信做完前面那题，现在看这个题会感觉到比较简单，都是一个套路。用二分求一个最小，。然后用check函数去判断这个最小是否可以满足最大的条件。思路和上题几乎一样且更加清晰，代码注释我都给的比较详细，大家可以认真看看。

细节：这里要考虑的就是check部分的除法。假设n=6,现在要去分的数组有14和12，如果直接//，那么14那个数组的值是小的，因为余数2也算一组。那这个常用的办法就是对被除数去改变，对其去加减常数从而符合题意。我代码给的办法大家可以直接记忆，再遇到这种需要对任意数除法得到永远进位的商的情况是很好用的。

例题5 — 1760.袋子里最少数目的球

给你一个整数数组 nums ，其中 nums[i] 表示第 i 个袋子里球的数目。同时给你一个整数 maxOperations 。

你可以进行如下操作至多 maxOperations 次：

• 选择任意一个袋子，并将袋子里的球分到 2 个新的袋子中，每个袋子里都有 正整数 个球。
  • 比方说，一个袋子里有 5 个球，你可以把它们分到两个新袋子里，分别有 1 个和 4 个球，或者分别有 2 个和 3 个球。

你的开销是单个袋子里球数目的 最大值 ，你想要 最小化 开销。

请你返回进行上述操作后的最小开销。

示例 1：

输入：nums = [9], maxOperations = 2
输出：3
解释：
- 将装有 9 个球的袋子分成装有 6 个和 3 个球的袋子。[9] -> [6,3] 。
- 将装有 6 个球的袋子分成装有 3 个和 3 个球的袋子。[6,3] -> [3,3,3] 。
装有最多球的袋子里装有 3 个球，所以开销为 3 并返回 3 。

示例 2：

输入：nums = [2,4,8,2], maxOperations = 4
输出：2
解释：
- 将装有 8 个球的袋子分成装有 4 个和 4 个球的袋子。[2,4,8,2] -> [2,4,4,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,4,4,4,2] -> [2,2,2,4,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,2,2,4,4,2] -> [2,2,2,2,2,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,2,2,2,2,4,2] -> [2,2,2,2,2,2,2,2] 。
装有最多球的袋子里装有 2 个球，所以开销为 2 并返回 2 。

示例 3：

输入：nums = [7,17], maxOperations = 2
输出：7

提示：

• 1 <= nums.length <= 105
• 1 <= maxOperations, nums[i] <= 109

class Solution:def minimumSize(self, nums: List[int], maxOperations: int) -> int:left, right = 1, max(nums)def can(mid):temp = 0for i in nums:temp += (i + mid - 1) // midreturn temp <= maxOperations + len(nums)while left <= right:mid = (left + right) >> 1if can(mid):right = mid - 1else:left = mid + 1return left

#思路

这题和上代码上几乎一样，思路也差不多，二分最小，can函数算最大条件。

假设最终每个袋子的球数都至多为 m，那么 m 越小，需要的袋子越多，操作次数也越多；m 越大，需要的袋子越少，操作次数也越少。有单调性，可以二分答案。或者说，看到「最小化最大值」就要先思考二分。

不难看出，每操作一次就多出一个袋子。那么我们可以二分遍历最大值，看看袋子数量是否满足操作次数加数组原本长度（因为是操作一次多一个袋子，所以是在原本长度上加一）。代码用的是闭区间写法。速度不是最快，算中等。感兴趣的同学可以自己去查其他题解。

细节

1、由于无法合并，所以除法和上题一样的，需要向上取整

2、左边界最小就是1，不可能是0，如果最大值是0那就没有数组的值了；右边界是数组原本最大值，即没有操作次数的情况。

3、最大化最小值

和上题相反，这题是二分答案求最大。二分的 mid 表示下界，即函数为下界条件判断。

例题6 — 3281.范围内整数的最大得分值

给你一个整数数组 start 和一个整数 d，代表 n 个区间 [start[i], start[i] + d]。

你需要选择 n 个整数，其中第 i 个整数必须属于第 i 个区间。所选整数的 得分 定义为所选整数两两之间的 最小 绝对差。

返回所选整数的 最大可能得分 。

示例 1：

输入： start = [6,0,3], d = 2

输出： 4

解释：

可以选择整数 8, 0 和 4 获得最大可能得分，得分为 min(|8 - 0|, |8 - 4|, |0 - 4|)，等于 4。

示例 2：

输入： start = [2,6,13,13], d = 5

输出： 5

解释：

可以选择整数 2, 7, 13 和 18 获得最大可能得分，得分为 min(|2 - 7|, |2 - 13|, |2 - 18|, |7 - 13|, |7 - 18|, |13 - 18|)，等于 5。

提示：

• 2 <= start.length <= 105
• 0 <= start[i] <= 109
• 0 <= d <= 109

class Solution:def maxPossibleScore(self, start: List[int], d: int) -> int:start.sort()def check(score: int) -> bool:x = -inffor s in start:x = max(x + score, s)  # x 必须 >= 区间左端点 sif x > s + d:return Falsereturn Trueleft, right = 0, (start[-1] + d - start[0]) // (len(start) - 1) + 1while left + 1 < right:mid = (left + right) // 2if check(mid):left = midelse:right = midreturn left

#思路

这题一开始想错了，因为没认真看题。大家注意看示例2，每个数两两之间都要去操作，所以就和顺序无关，可以用贪心的想法去做。这里给大家分享一下灵神的写法。

题意
给你 n 个一样长的区间，每个区间选一个数，最大化得分。得分即所选数字中的任意两数之差的最小值。

二分答案
假设得分为 score。

把区间按照左端点排序。这样我们只需考虑相邻区间所选数字之差。

设从第一个区间选了数字 x，那么第二个区间所选的数字至少为 x+score，否则不满足得分的定义。

由于得分越大，所选数字越可能不在区间内，有单调性，可以二分答案。

或者说，看到「最大化最小值」就要先思考二分。

贪心
现在问题变成：

给定 score，能否从每个区间各选一个数，使得任意两数之差的最小值至少为 score。
⚠注意：这里是至少，不是恰好，两数之差的最小值可以不等于 score。由于二分会不断缩小范围，最终一定会缩小到任意两数之差的最小值恰好等于 score 的位置上。

把区间按照左端点排序。第一个数选谁？

贪心地想，第一个数越小，第二个数就越能在区间内，所以第一个数要选 x0=start[0]。

如果第二个数 x1=x0+score 超过了区间右端点 start[1]+d，那么 score 太大了，应当减小二分的右边界 right。

如果 x1​≤start[1]+d，我们还需要保证 x1​ 大于等于区间左端点 start[1]，所以最终

依此类推，第 i 个区间所选的数为

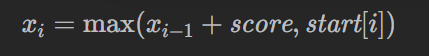
必须满足

如果所有选的数都满足上式，那么增大二分的左边界 left。

细节
下面代码采用开区间二分，这仅仅是二分的一种写法，使用闭区间或者半闭半开区间都是可以的。

开区间左端点初始值：0。一定可以选出 n 个数，两两之差都大于等于 0。
开区间右端点初始值：

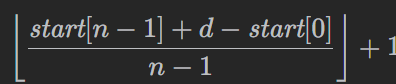
最小值不会大于平均值，所以比平均值更大的数必然无法满足要求。
对于开区间写法，简单来说 check(mid) == true 时更新的是谁，最后就返回谁。相比其他二分写法，开区间写法不需要思考加一减一等细节，更简单。推荐使用开区间写二分。

代码实现时，可以假设第一个区间左边还选了一个数 −∞，这样不影响答案且代码更简洁。

4、第 K 小/大

什么是第K小/大呢？给大家举个例子理解一下

例如数组 [1,1,1,2,2]，其中第 1 小、第 2 小和第 3 小的数都是 1，第 4 小和第 5 小的数都是 2。

第 k 小等价于：求最小的 x，满足 ≤x 的数至少有 k 个。
第 k 大等价于：求最大的 x，满足 ≥x 的数至少有 k 个。

注 1：一般规定 k 从 1 开始，而不是像数组下标那样从 0 开始。

注 2：部分题目也可以用堆解决。

例题7 — 668.乘法表中第k小的数（困难）

几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第 k 小的数字吗？

乘法表是大小为 m x n 的一个整数矩阵，其中 mat[i][j] == i * j（下标从 1 开始）。

给你三个整数 m、n 和 k，请你在大小为 m x n 的乘法表中，找出并返回第 k 小的数字。

示例 1：

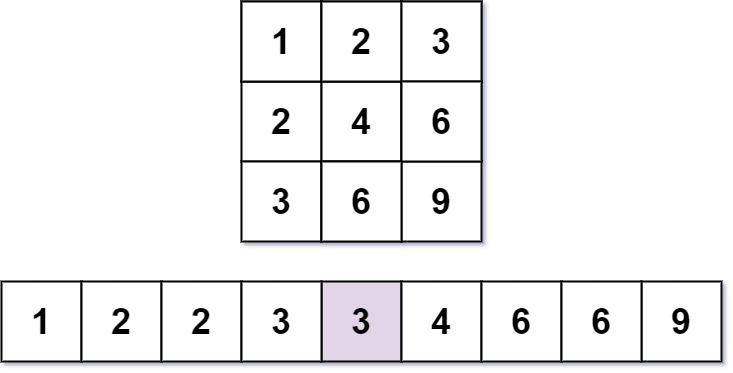
输入：m = 3, n = 3, k = 5
输出：3
解释：第 5 小的数字是 3 。

示例 2：

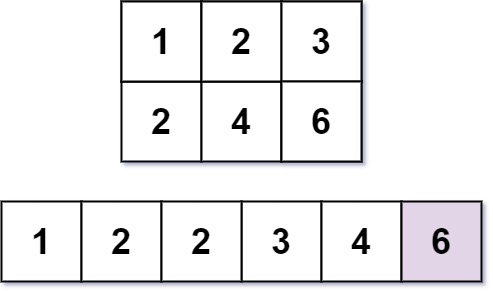
输入：m = 2, n = 3, k = 6
输出：6
解释：第 6 小的数字是 6 。

提示：

• 1 <= m, n <= 3 * 104
• 1 <= k <= m * n

class Solution(object):def findKthNumber(self, m, n, k):""":type m: int:type n: int:type k: int:rtype: int"""def can(mid):temp = 0for i in range(1, m + 1):temp += min(n, mid // i)return temp >= k left, right = 1, m * n - 1while left <= right:mid = (left + right) >> 1if can(mid):right = mid - 1else:left = mid + 1return left

#思路

越短的题目越难，相信大家看完这题之后深有体会。类似这种题目，我会想到两种思路。要么用代码的方法，转换形式去强行计算；要么就用数学的方式写判断函数，因为这题的内容本身就是用数学公式搞出来的。

这里给大家看看灵神的思路，确实代码看着简单，但是理解起来还是蛮费劲的。

第 k 小/大问题的通用转化方法：

第 k 小等价于：求最小的 x，满足 ≤x 的数至少有 k 个。（注意是至少不是恰好，因为等于k可以有多个数。不用担心出现不等于第k小或者大的情况，因为二分总是会遍历到一个符合的答案（只要范围包括了这个数，那肯定会被遍历到的））
第 k 大等价于：求最大的 x，满足 ≥x 的数至少有 k 个。
对于本题，x 越大，越能找到 k 个数；x 越小，越不能找到 k 个数。据此，可以二分猜答案。

现在本题转化成一个判定性问题：

给定整数 x，统计乘法表中 ≤x 的元素个数 cnt，判断是否满足 cnt≥k。
从第 1 行到第 m 行，我们一行一行地遍历乘法表。

第 i 行的数都是 i 的倍数，其中有多少个 ≤x 的正整数？

那么我们在行上去遍历，然后累加每列小于mid的数有几个，最后得到的值如果比k大说明mid太大了，导致比他小的数太多了，如果小，说明mid太小了。

细节
如果写闭区间二分，左右边界是 [1,mn−1]，注意 mn 不需要在二分区间内，因为如果我们没有在 [1,mn−1] 中找到答案，那么答案就一定是 mn。

答疑
问：为什么二分结束后，答案 ans 一定在乘法表中？

答：反证法。假设 ans 不在乘法表中，这意味着乘法表中第 k 小的数比 ans 小，或者说 ≤ans−1。换句话说，≤ans−1 的数有 k 个，即 check(ans−1)=true。但根据循环不变量，二分结束后 check(ans−1)=false，矛盾。故原命题成立。

注：由于作者写的时候脑抽了，开的python解释器还没发现，所以上述代码和正常python3的代码有点不一样，就这题会这样，其他的都不会；另外，上诉方法还可以继续优化，由于篇幅关系，这里就不介绍了，感兴趣的同学可以去看看这题的完整题解。

例题8 — 378.有序矩阵中第k小的元素

给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是 排序后 的第 k 小元素，而不是第 k 个 不同 的元素。

你必须找到一个内存复杂度优于 O(n2) 的解决方案。

示例 1：

输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13

示例 2：

输入：matrix = [[-5]], k = 1
输出：-5

提示：

• n == matrix.length
• n == matrix[i].length
• 1 <= n <= 300
• -109 <= matrix[i][j] <= 109
• 题目数据 保证 matrix 中的所有行和列都按 非递减顺序 排列
• 1 <= k <= n2

进阶：

• 你能否用一个恒定的内存(即 O(1) 内存复杂度)来解决这个问题?
• 你能在 O(n) 的时间复杂度下解决这个问题吗?这个方法对于面试来说可能太超前了，但是你会发现阅读这篇文章（ this paper ）很有趣。

class Solution:def kthSmallest(self, matrix: List[List[int]], k: int) -> int:n = len(matrix) # 注意题目给的条件 这个矩阵是n*n的def can(mid):i, j = 0, n - 1temp = 0while  j >= 0 and i < n and temp < k: # 在这题i和j都是单向的，所以只用做这两个条件判断。另外如果temp=k就不用继续遍历了，此时这个mid肯定满足条件，这样节省时间if matrix[i][j] <= mid: # 注意这里别搞混了，我们要找的是小于等于mid的数有几个i += 1temp += j + 1else:j -= 1return temp >= kleft, right = matrix[0][0], matrix[-1][-1] # 根据大小关系得出while left <= right:mid = (left + right) >> 1if can(mid):right = mid - 1else:left = mid + 1return left

#思路

这题和上题虽然属于一个题型，但构造却不一样。上题的数据之间是有数学关系的，那么我们就可以抓住其关系来求解。这题给的则是大小关系，那么同样，我们也可以根据大小关系来求解。给大家一个启发的点，我们想二分题目的时候，可以从答案往结果想，这样你的思路就会去想怎么构建check函数，而不是正面去想，怎么去直接找到这个数的位置。这样的思路有种动态规划的感觉。

第一次没写出来也不要紧，这些题目其实都蛮有特点的，可以练完之后自己总结一下，后面再看到类似的题目，就会有思路，毕竟这只是平常的练习，又不是考试。这题同样给出灵神的题解，双指针+二分的解法非常巧妙，完成了第一个进阶挑战。但是第二个挑战我看了半天，好想没有什么特别好的题解，就不给大家展示了，如果有兴趣的同学可以自己去深入思考一下。（我代码的注释记得认真看）

第 k 小/大问题的通用转化方法：

第 k 小等价于：求最小的 x，满足 ≤x 的数至少有 k 个。（注意是至少不是恰好）
第 k 大等价于：求最大的 x，满足 ≥x 的数至少有 k 个。
x 越大，越能找到 k 个数；x 越小，越不能找到 k 个数。据此，可以二分猜答案。

现在本题转化成一个判定性问题：

• 给定整数 mx，统计有序矩阵中 ≤mx 的元素个数 cnt，判断是否满足 cnt≥k。

如何高效统计 cnt 呢？

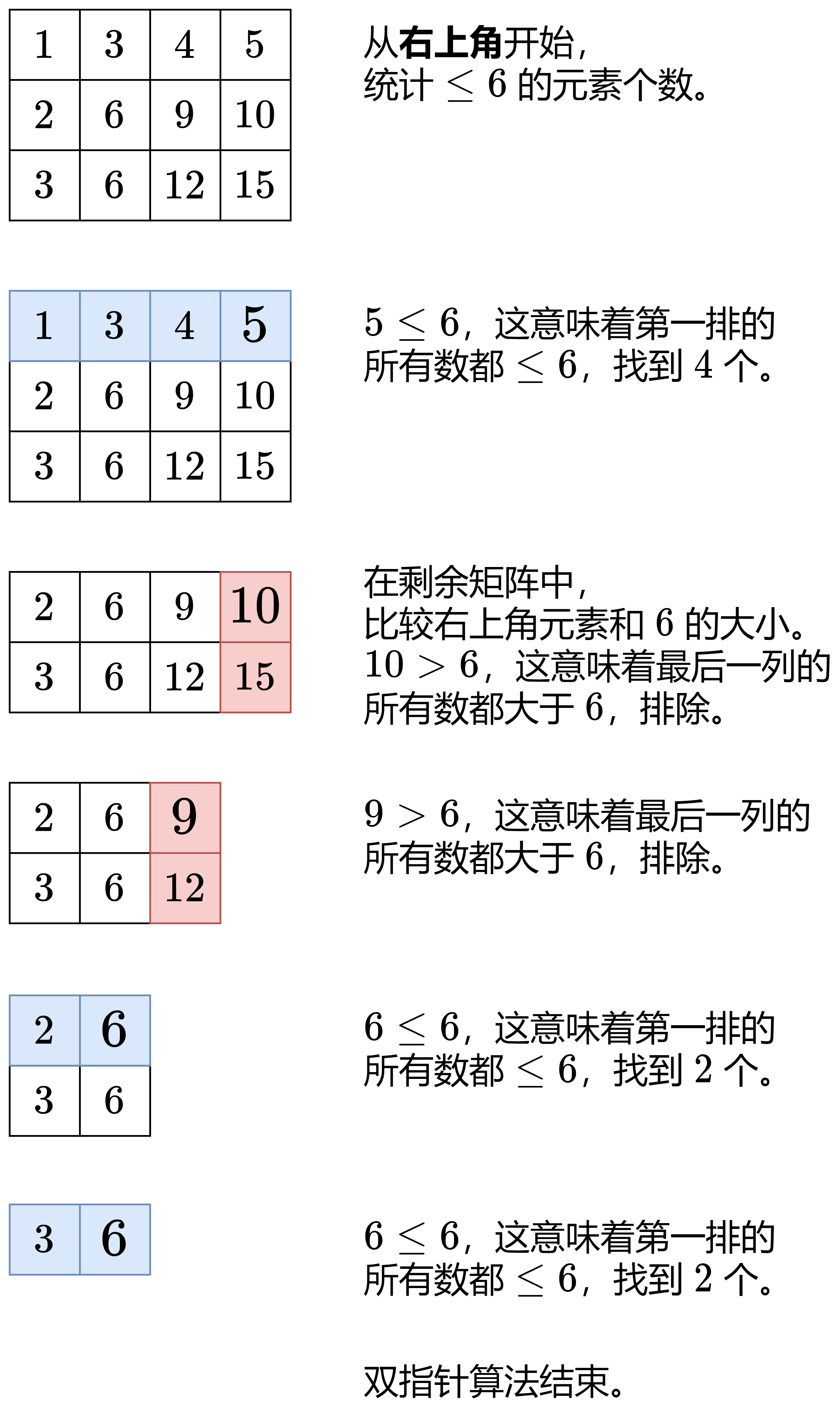
细节
下面代码采用开区间二分，这仅仅是二分的一种写法，使用闭区间或者半闭半开区间都是可以的，喜欢哪种写法就用哪种。

开区间左端点初始值：matrix[0][0]−1。不存在比最小值还小的数，也就是有 0 个数 ≤matrix[0][0]−1，由于 0<k，所以无法满足要求。
开区间右端点初始值：matrix[n−1][n−1]。有 n ^2个数 ≤matrix[n−1][n−1]，由于 n ^2 ≥k，所以一定满足要求。
对于开区间写法，简单来说 check(mid) == true 时更新的是谁，最后就返回谁。相比其他二分写法，开区间写法不需要思考加一减一等细节，更简单。推荐使用开区间写二分。(我给的代码是闭区间的写法，因为我比较喜欢hhh)

答疑
问：为什么二分结束后，答案 ans 一定在矩阵中？

答：反证法。假设 ans 不在矩阵中，这意味着矩阵中第 k 小的数比 ans 小，或者说 ≤ans−1。换句话说，≤ans−1 的数有 k 个，即 check(ans−1)=true。但根据循环不变量，二分结束后 check(ans−1)=false，矛盾。故原命题成立。（关于反法的类似讲解可以看我上一篇文章）

例题9 — 719. 找出第k小的数对距离（困难）

数对 (a,b) 由整数 a 和 b 组成，其数对距离定义为 a 和 b 的绝对差值。

给你一个整数数组 nums 和一个整数 k ，数对由 nums[i] 和 nums[j] 组成且满足 0 <= i < j < nums.length 。返回 所有数对距离中 第 k 小的数对距离。

示例 1：

输入：nums = [1,3,1], k = 1
输出：0
解释：数对和对应的距离如下：
(1,3) -> 2
(1,1) -> 0
(3,1) -> 2
距离第 1 小的数对是 (1,1) ，距离为 0 。

示例 2：

输入：nums = [1,1,1], k = 2
输出：0

示例 3：

输入：nums = [1,6,1], k = 3
输出：5

提示：

• n == nums.length
• 2 <= n <= 104
• 0 <= nums[i] <= 106
• 1 <= k <= n * (n - 1) / 2

class Solution:def smallestDistancePair(self, nums: List[int], k: int) -> int:nums.sort()def can(mid):temp = 0i = 0for j, x in enumerate(nums):while x - nums[i] > mid:i += 1temp += j - i return temp >= kleft, right = 0, nums[-1] - nums[0]while left <= right:mid = (left + right) >> 1if can(mid):right = mid - 1else:left = mid + 1return left

#思路

这题还是二分+双指针，正好把前面练过的东西回顾了一下。整体思路大概是，对于这种涉及数值排序的题目，可以先看看原数组的顺序是否重要，如果不重要，那我们就可以去排序，可以把按步的操作转化为数学操作，会简单很多。这题便是这样因为每个数可以和任意位置的任意数相减，只要不重复。那么排序后可以得出，在左右端点固定并且二者相减满足条件的情况下，子数组内的任意数操作后的值都一定满足条件。

但看出这点只是第一步，如果你就这样去找一个子数组并且把其内部数按照累加的方式（1+2+3+4这样）去计算一个结果的话，那就大错特错了。eg：如果有数组1，2，3，4，5；假设1，4符合条件，那么2，5也是符合条件的，如果1，5不符合条件，那按照上述方法就会得到错误结论。所以想到这里就很明显能发现，这是双指针的问题。在右端点固定是，要找到一个左端点，使得二者相减满足条件。在个过程中两个指针会不断的向右侧移动，产生不同的子数组。那么这个时候就要去考虑怎么对这些算出来的子数组去计数。像我们上面那样肯定不行，会有重复。比如上面那个例子的2，3和2，4和3，4就是重复计算了，但这也可以看出我们在每子数组计算的时候只需要动左端点就行，即算一遍过去，这样就不会重复或者遗漏（类似我给的例子，1，4的子数组没算的点，2，5的会算到）

以下是详细思路讲解

转化
第 k 小/大问题的通用转化方法：

第 k 小等价于：求最小的 x，满足绝对差 ≤x 的数对至少有 k 个。（注意是至少不是恰好）
第 k 大等价于：求最大的 x，满足绝对差 ≥x 的数对至少有 k 个。
对于本题，x 越大，越能找到 k 个数对；x 越小，越不能找到 k 个数对。据此，可以二分猜答案。

现在本题转化成一个判定性问题：

给定整数 mx，统计绝对差 ≤mx 的数对个数 cnt，判断是否满足 cnt≥k。
如何高效统计 cnt 呢？

同向双指针
为方便计算，把 nums 从小到大排序。

排序后，nums[j] 越大，那么满足 i<j 且 nums[j]−nums[i]≤mx 的最小的 i 也越大，我们可以用同向双指针解决这个问题。外层循环枚举 nums[j]，内层循环若 i 不满足上式，就把 i 加一。

内层循环结束后，下标对 (i,j) 是满足要求的。由于 i 越大越能满足要求，所以除了 (i,j)，还有 (i+1,j),(i+2,j),…,(j−1,j) 都是满足要求的。也就是说，当 j 固定时，i,i+1,i+2,…,j−1 都是满足要求的，这一共有 j−i 个，加到 cnt 中。

细节
下面代码采用闭区间二分，这仅仅是二分的一种写法，使用开区间或者半闭半开区间都是可以的，喜欢哪种写法就用哪种。（这块的条件在题目的提示部分有写）

开区间左端点初始值：−1。绝对差不能是负数，也就是有 0 个数对 ≤−1，由于 0<k，所以无法满足要求。
开区间右端点初始值：排序后的 nums[n−1]−nums[0]。所有数对都满足要求，这有  n(n−1)/2个，由于 n(n−1)/2≥k，所以一定满足要求。
对于开区间写法，简单来说 check(mid) == true 时更新的是谁，最后就返回谁。相比其他二分写法，开区间写法不需要思考加一减一等细节，更简单。推荐使用开区间写二分。

答疑
问：为什么二分结束后，答案 ans 一定是 nums 中的某两个数的绝对差？

答：反证法。假设 ans 不是某两个数的绝对差，这意味着第 k 小的绝对差比 ans 小，或者说 ≤ans−1。换句话说，≤ans−1 的数对有 k 个，即 check(ans−1)=true。但根据循环不变量，二分结束后 check(ans−1)=false，矛盾。故原命题成立。

第k大的题有点太难了，等我二刷再写吧，想看的朋友可以自己去搜索一下QAQ

5、其他

这块题目就比较杂了，没有什么特点，但相较于前面的题目会比较灵活，也可以拿来练练手。

例题10 — 69.x的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

• 0 <= x <= 231 - 1

class Solution:def mySqrt(self, x: int) -> int:left = 1if x > 4:right = x // 2else:right = xwhile left <= right:mid = (left + right) >> 1 # 这里的位运算相当于向下取整的除二if mid * mid > x:right = mid - 1elif mid * mid == x:right = midbreakelse:left = mid + 1return right

#思路

这题是道比较简单的。题目说没法用函数直接算出答案，那我们就可以想到用二分猜答案。因为对于非负整数 m 来说，由于 m 越小越满足 m2≤x，m 越大越不满足 m2≤x，有单调性，可以二分答案。

但是这题我在原本闭区间的写法上做了一点修改。原本要返回的是left，并且判断分支我也改成了3个，一个是为了答案正确，一个是为了加速判断（但好像大家的方法做出来都是3ms，没啥区别。。。）至于为什么要这么做，具体的大家可以自己去画画这两个例子，一个是x=8，一个是x=4.

左端点是1，因为这是最小的非负整数（提示里面有提到x>=0），右端点我们可以去做严格的数学证明，说明在x>4的时候，x的算术平方根是一定小于x的一半。由于题目要的是向下取整的整数，所以当x>4的时候x的一半可能是答案（假设答案是2.34，那就要返回2，而x的一半是2.45，做除法是向下取整的，所以这个值也是2。故此时x的一半一定包含着答案）

以下是数学证明

例题11 — 74.搜索二维矩阵

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

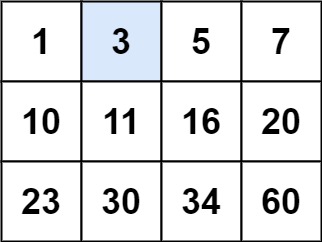
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

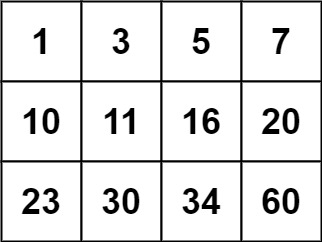
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:n = len(matrix[0])m = len(matrix)left = 0right = m * n - 1while left <= right:mid = (left + right) >> 1if matrix[mid // n][mid % n] > target:right = mid - 1elif matrix[mid // n][mid % n] == target:return Trueelse:left = mid + 1return False

#思路

这题其实我一开始想到的方法类似于排除法，因为这个矩阵的单调性太好了，我们完全可以先通过最后一个数，确定target在哪一行，然后再在那一行去找。但是这个过程需要两个二分去查找下标。所以后面灵机一动，又想到了这个标准的二分方法。其实题目写多了，对于这种矩阵的处理方式也是了然于胸，要么下标要么双指针。显然，这题可以通过数学方法去处理下标，使得矩阵可以转化为列表。

由于矩阵的每一行是递增的，且每行的第一个数大于前一行的最后一个数，如果把矩阵每一行拼在一起，我们可以得到一个递增数组。有单调性就可以用二分。

例如示例 1，三行拼在一起得

a=[1,3,5,7,10,11,16,20,23,30,34,60]
由于这是一个有序数组，我们可以用二分查找判断 target 是否在 matrix 中。

代码实现时，并不需要真的拼成一个长为 mn 的数组 a，而是将 a[i] 转换成矩阵中的行号和列号。例如示例 1，i=9 对应的 a[i]=30，由于矩阵有 n=4 列，所以 a[i] 在 ⌊ i/n⌋=2 行，在 imodn=1 列。

一般地，有

a[i]=matrix[⌊i/n⌋][i mod n]

我用的是闭区间写法，其他方法也是一样的。

例题12 — 852.山脉数组的峰顶索引

给定一个长度为 n 的整数 山脉 数组 arr ，其中的值递增到一个 峰值元素 然后递减。

返回峰值元素的下标。

你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。

示例 1：

输入：arr = [0,1,0]
输出：1

示例 2：

输入：arr = [0,2,1,0]
输出：1

示例 3：

输入：arr = [0,10,5,2]
输出：1

提示：

• 3 <= arr.length <= 105
• 0 <= arr[i] <= 106
• 题目数据 保证 arr 是一个山脉数组

class Solution:def peakIndexInMountainArray(self, arr: List[int]) -> int:left, right = 1, len(arr) - 2while left <= right:mid = (left + right) >> 1if arr[mid] > arr[mid - 1] and arr[mid] > arr[mid + 1]:return midelif arr[mid] > arr[mid + 1]:right = mid - 1else:left = mid + 1return left

#思路

根据题意，arr 在左右两侧递增的时候没有重复元素，且峰顶的下标一定在区间 [1,n−2] 中。

比较 arr[i] 和 arr[i+1] 的大小关系：

上坡：如果 arr[i]<arr[i+1]，那么峰顶下标 >i。
下坡：如果 arr[i]>arr[i+1]，那么峰顶下标 ≤i。
由于随着 i 的变大，arr[i]>arr[i+1] 会从「不成立」变成「成立」，有单调性，就能二分。

可以在二分的途中写一个判断是否刚好满足题意的语句，可以省一点空间。

例题13 — 寻找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

提示：

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• nums 中的所有整数 互不相同
• nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

class Solution:def findMin(self, nums: List[int]) -> int:left, right = 0, len(nums) - 2while left <= right:mid = (left + right) >> 1if nums[mid] < nums[-1]:right = mid - 1else:left = mid + 1return nums[left]

#思路

这题还蛮有意思的，也是一个数学思考的过程。大家可以发现，无论怎么旋转，这个数组都只会是单调的，要么整体单调，要么分成两部分单调。这时候就可以思考用二分的方法。但是大家不能局限在这个单调的数组中。因为仅凭这个信息还写不出来left和right的移动条件。我们需要想到一个判断方法使得循环一直在一个正确的区间内。那么如何判断mid该向左还是向右呢？

这里给大家一个思路，反正大家记住就行，有个印象，后面再碰到类似的题目就有想法了。

‘设 x=nums[mid] 是现在二分取到的数。

我们需要判断 x 和数组最小值的位置关系，谁在左边，谁在右边？

把 x 与最后一个数 nums[n−1] 比大小：

如果 x>nums[n−1]，那么可以推出以下结论：
nums 一定被分成左右两个递增段；
第一段的所有元素均大于第二段的所有元素；
x 在第一段。
最小值在第二段。
所以 x 一定在最小值的左边。
如果 x≤nums[n−1]，那么 x 一定在第二段。（或者 nums 就是递增数组，此时只有一段。）
x 要么是最小值，要么在最小值右边。
所以，只需要比较 x 和 nums[n−1] 的大小关系，就间接地知道了 x 和数组最小值的位置关系，从而不断地缩小数组最小值所在位置的范围，二分找到数组最小值。’

这里闭区间二分的right的范围需要注意一下，不能是n-1，大家去画个图就知道了，如果设为n-1，left会超出index（因为如果答案是right的话，left会到right+1才能停下来）

6、结语

大家可能会发现这次分的部分还挺多，但是题目却没有太多，是因为我刷的题单里面有些题目确实是太难了，或者有些重要的知识点没有涉及到亦或者是题目太简单。我现在给出来的题目，最难的评分大概都在2000左右，难度都不会太夸张，所以有些题目可能等二刷的时候才会涉及。其实这些题目对应一些算法比赛也够了，难度其实都差不多，除非你是冲着国奖去的，否则也没必要太较劲。其实去公司面试的时候那些题目也不会太难差不多能把中等的题目短时间内大致写出来的水平就可以了。

另外大家可能注意到了，二分只是一个通用的模版，其实写到后面，真正难的不是二分的写法，而是check函数要怎么写，即怎么转换题目的条件判断。所以接下来的题单会去练习一下一些技巧。下一章我选的内容是——贪心。

那么本期笔记就到这里啦，有任何问题可以评论区打出，我看到就会回复哒～

大家一起加油！！！